Prestack Rank-Reduction-Based Noise Suppression

Abstract

Prestack random-noise suppression is an important but inadequately- solved problem in land seismic processing, with the potential to significantly improve AVO analysis and the stacked section. To address this problem, we describe a family of filters that perform matrix-rank reduction on constant-frequency slices. These filters include two existing techniques – eigenimage and Cadzow filtering – as well as a novel hybrid method with properties from both. This general class of noise suppressors is powerful, versatile, and can be applied in any number of spatial dimensions. We explain the theory behind these filters, and demonstrate how to apply them in practice.

1. Introduction

Prestack random-noise suppression is important for improving amplitude variation with offset (AVO) and azimuthal (AVAZ) analysis, but it can also improve the stacked section by exploiting the larger volume of data available at the prestack stage, by allowing for improved velocity analysis and statics correction, and by cleaning up multiples prior to their removal.

But prestack random-noise suppression is a difficult problem, with complications including very low signal-to-noise ratios, residual statics, imperfect normal-moveout (NMO) correction, non-uniformly-spaced traces, the need to preserve multiples (so that multiple removal is not hampered later) and subtle amplitude anomalies of critical importance to AVO and AVAZ analysis. These complications are particularly acute for land and transition-zone seismic.

Thus an ideal prestack noise suppressor should have the following properties:

• Strength can be varied easily, with the ability to make it extremely powerful or mild.
• Handles non-uniformly-spaced shots.
• Handles 2-D, 3-D, and 4-D data.
• Handles plains and structured data.
• Preserves multiples, under- and over-corrected events, and diffractions.
• Preserves AVO and AVAZ effects.
• Does not create artifacts (artificial events).
• The output is in the same spatial domain as the input. In particular, the output is unstacked.
• Works in any number of spatial dimensions simultaneously, since higher spatial dimensions increase the ability to simultaneously preserve signal and remove noise.

Given this daunting list of requirements, it’s not surprising that no approach developed so far has been entirely satisfactory. Our goal is to ameliorate this.

We begin by describing two existing methods, namely eigenimage and Cadzow filtering, which perform matrix-rank reduction on constant-frequency slices. We show how these filters can be hybridized to form a more general and useful class of methods with attributes of both. We then demonstrate how these methods are applied to real data. Finally we discuss their behavior in the presence of AVO and AVAZ effects, how they might be used to filter timelapse data, and their resistance to artifacts.

2. The Filters and Their Properties

The filters we will describe use a noise-suppression strategy called “matrix-rank reduction” (see, for example, Trickett 2003), also called truncated singular-value decomposition, principalcomponent analysis, subspace filtering, and many other names.

The singular-value decomposition, described in the previous reference, allows one to decompose a p-by-p matrix A into the sum of p matrices of rank one, called weighted eigenimages:

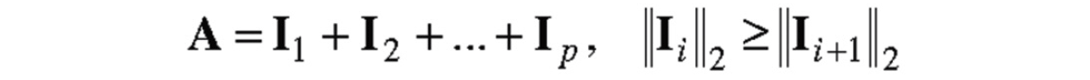
A rank-k approximation to matrix A can be found by summing the first k < p weighted eigenimages:

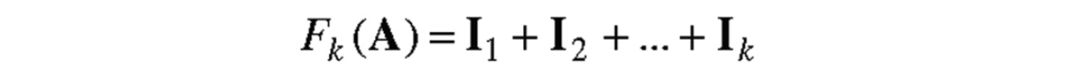
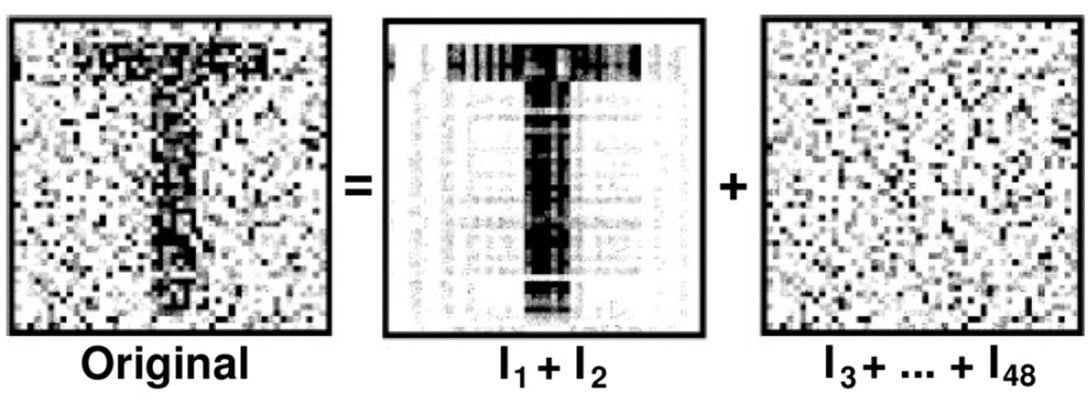
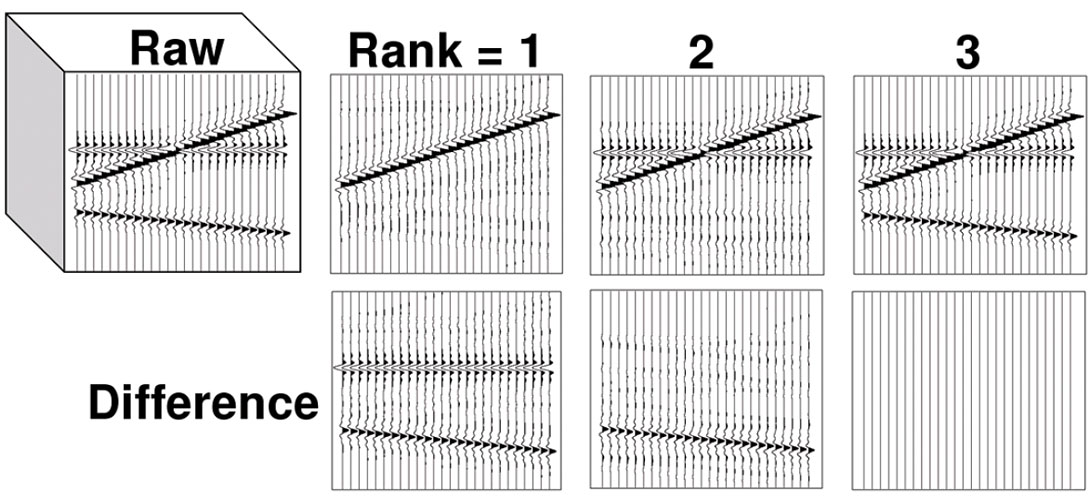
Rank reduction is a useful tool for noise suppression as coherent energy tends to fall into the first few eigenimages, while random energy is more evenly distributed across all eigenimages. Thus a rank-k approximation preserves coherency while eliminating randomness (Figure 1). Rank reduction is not new to the geophysical industry. It is used in Karhunen-Loeve and spectral-matrix filtering, multiple attenuation, velocity analysis, acquisition-footprint removal, and many other applications.

Here we describe a family of rank-reduction filters that work on constant-frequency slices. For a multi-dimensional grid of traces, the general method is given in Table 1.

The only difference between the various techniques discussed here is how matrix A is formed in step 1.

Eigenimage Filtering

Ulrych et al (1999) described seismic applications for eigenimage filtering. Trickett (2003) applied eigenimage filtering in the f-xy domain (f representing frequency, x and y representing two spatial dimensions) as follows:

Suppose we have an n-by-n grid of traces. To simplify the discussion we assume square grids, but rectangular grids work just as well. For a given frequency, let the complex values from a constant-frequency slice of this grid have values c_i,j, i=1...n, j=1…n. In the method shown in Table 1, set

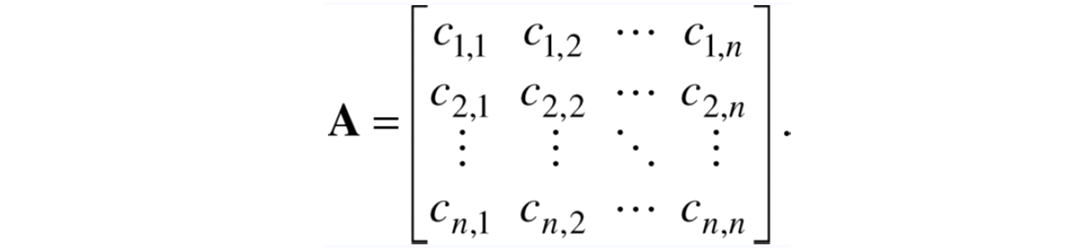
Averaging in step 3 of Table 1 is unnecessary, as each trace has only one entry in the matrix. F-xy eigenimage filtering, as this is called, was shown to have the following properties (Grimm et al, 2003; Trickett, 2003):

Exactness Property: If a grid of seismic traces is noiseless and is the sum of plane waves having no more than k distinct dips, then f-xy eigenimage filtering with rank k does nothing.

The exactness property suggests these filters handle structured data as easily as plains data. Although this property seems to suggest that only a few dips will be preserved, in practice even curving reflectors are accurately modeled with moderate rank. If the data contains more than k distinct dips then a rank-k filter tends to preserve the k most energetic dips. See Figure 2.

Shooting Property: If a grid of seismic traces is noiseless and contains no more than k dips when viewed in the CMP domain, then f-xy eigenimage filtering with rank k does nothing when the x-y coordinates represent common source and receiver.

The shooting property does not require that source and receiver locations be uniformly spaced. Indeed they can be positioned randomly.

Statics Property: F-xy eigenimage filtering is independent of x- and yconsistent statics.

The statics property is quite remarkable as it asserts that noise attenuation in the presence of surface-consistent statics is equivalent to noise attenuation after the correction of these statics. We know of no other noise filter that can handle large statics.

Filtering Property: If a noiseless seismic section contains no more than k dips, and then has x- and y-consistent filters applied, then f-xy eigenimage filtering with rank k does nothing.

This suggests that we may be able to apply eigenimage filtering before surface-consistent deconvolution.

None of these properties hold when eigenimage filtering is applied to constant time slices in the time domain, which is why the frequency domain is much preferred.

F-xy eigenimage filtering thus appears ideal for prestack noise suppression, particularly when the x and y coordinates represent source and receiver. But this filter is rarely used due to two limitations. First, the f-xy eigenimage filter can only easily be applied in two dimensions. One-dimensional eigenimage filtering does nothing. Three-dimensional eigenimage filtering is best done using multilinear rather than linear algebra–that is to say, performing rank reduction on tensors rather than matrices (De Lathauwer, et al, 2000; Wang, 2007). Multilinear algebra theory is not as elegant nor straightforward as linear algebra, and we generally like to avoid it. Second, f-xy eigenimage filtering is rather weak. Making it stronger can require reducing the rank to the point of removing signal.

Cadzow Filtering

Suppose we have a one-dimensional series of n traces whose values along a constant-frequency slice are c_i, i=1…n. F-x Cadzow filtering (Cadzow, 1988; Trickett, 2002) is achieved by setting

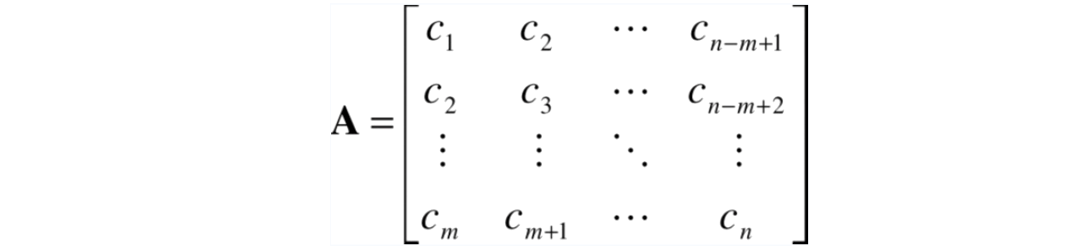
and performing rank reduction on matrix A as described in Table 1.

Variable m is usually set to half of n, making the matrix as square as possible. This is a Hankel matrix, meaning it is constant along each antidiagonal. Cadzow filtering was independently discovered several times, and so is also known as Singular Spectrum Analysis (SSA) and the Caterpillar method (Golyandina et al, 2001; Sacchi, 2009).

Trickett (2008) extended f-x Cadzow filtering to two spatial dimensions by forming a Hankel matrix of Hankel matrices

where

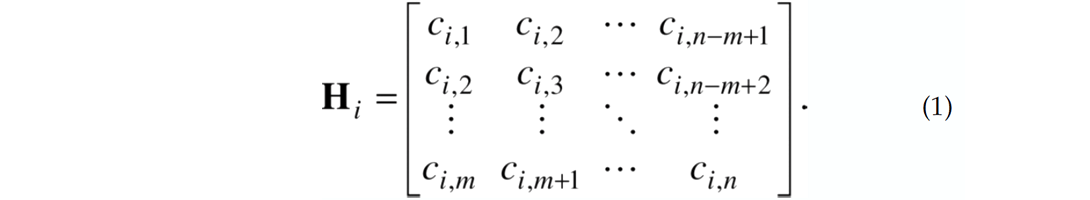
This matrix configuration has been used in applications outside of the seismic industry such as terrain modeling (Golyandina et al, 2007). F-xy filtering is better than f-x because it works with more data in a more local area, resulting in simultaneously more noise suppression and better signal preservation. Cadzow filtering can be extended to any number of spatial dimensions. Three dimensions, for example, are handled by forming a Hankel matrix of Hankel matrices of Hankel matrices.

Cadzow filtering has some advantages over eigenimage. Cadzow can be used in any number of spatial dimensions, as opposed to just two for eigenimage. It can also be made far stronger than eigenimage while still preserving conflicting dips. As a rough rule of thumb, Cadzow filtering gives a four-fold improvement in signal-to-noise ratio with each additional spatial dimension, assuming typical parameters are used. Thus higherdimensional Cadzow filtering is of great interest for very noisy areas. Unfortunately, Cadzow becomes much more computationally expensive with each added dimension.

The exactness property holds for any number of dimensions:

Exactness Property for n-dimensional Cadzow: Suppose a noiseless n-dimensional grid of traces is the sum of hyperplane waves with at most k distinct dips (where a dip is distinguished by its slope in all n dimensions). Then n-dimensional Cadzow filtering with a rank of k does nothing.

Cadzow filtering does not, however, have the shooting property. In particular, if the spatial coordinates represent sources and receivers then the sources and receivers should be uniformly spaced – a problem for land surveys. Nor does Cadzow have the filtering or statics properties, and so is best applied after deconvolution and surface-consistent statics correction.

Hybrid Filtering

We can hybridize eigenimage and Cadzow filtering to derive a new type of filter that is better suited than either for prestack applications. Suppose we have two spatial dimensions, and wish to treat the first as eigenimage and the second as Cadzow. Following Dologlou et al (1996), set

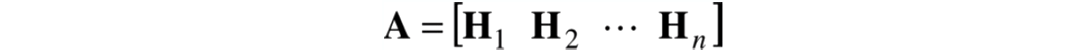
where H_i are the Hankel matrices from Equation 1. Since the Hankel matrices are symmetric or nearly so, it makes little difference if we append the Hankel matrices horizontally (as we’ve done here) or vertically. It would make a difference for strongly rectangular Hankel matrices.

If we have three spatial dimensions and wish to treat the first dimension as eigenimage and the remaining two as Cadzow, then replace the Hankel matrices above with Hankel matrices of Hankel matrices. To treat two dimensions as eigenimage and one as Cadzow, set

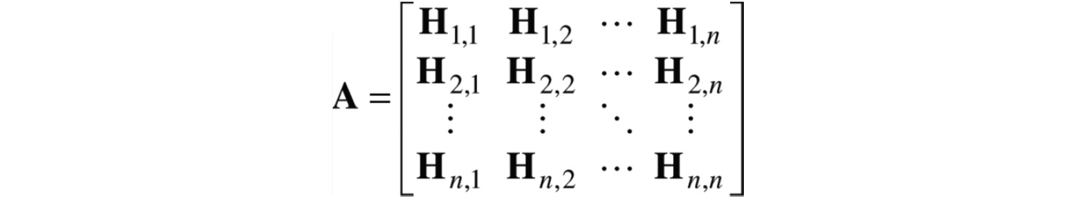
where H_i,j is the Hankel matrix for the i^th index of the first dimension and j^th index of the second. In four-spatial-dimensional filtering where two dimensions are eigenimage and two are Cadzow, H_i,j is a Hankel matrix of Hankel matrices.

As there are countless variations, we will use the notation E^pC^q to refer to a (p+q)-dimensional filter such that the first p dimensions are eigenimage and the remaining q dimensions Cadzow. Thus EC² is a hybrid filter with one dimension eigenimage and two Cadzow. C³ is a pure Cadzow filter in three dimensions. Figure 3 shows how a constant-frequency slice in two spatial dimensions is transformed to an E², EC and C² matrix A. Figure 4 shows how a constant-frequency cube (three spatial dimensions) is transformed to a C³ matrix.

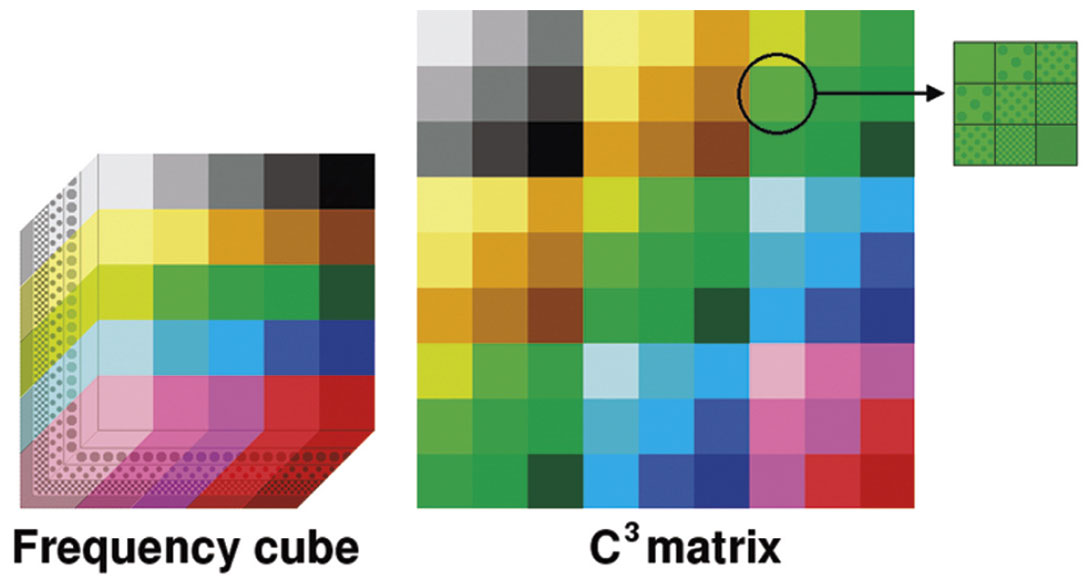
The exactness property holds for the hybrid filters. Dimensions that are treated as eigenimage have all the properties of eigenimage filtering. If one of the dimensions, for example, represents common source and is treated as eigenimage then we do not require source locations to be uniformly spaced and can tolerate source-consistent statics. Those dimensions treated as Cadzow, however, should be uniformly spaced and not contain large statics.

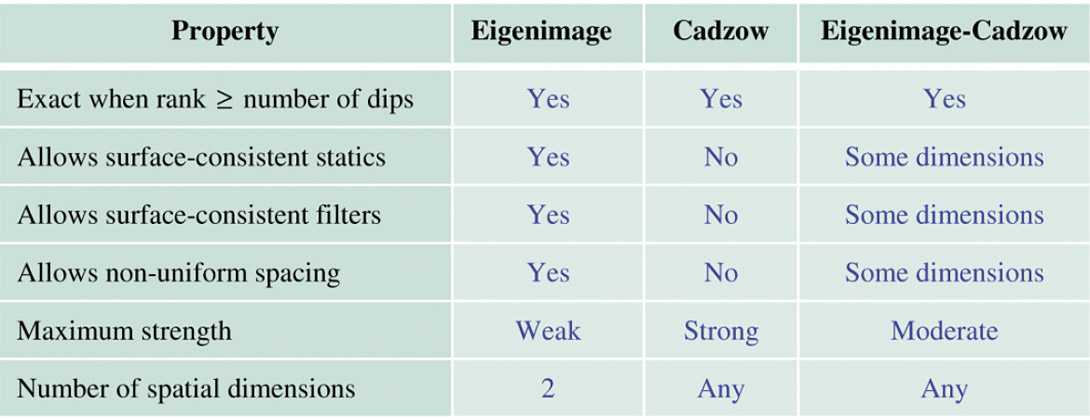
Hybrid filters fall between Cadzow and eigenimage filtering in strength. For instance, C² filtering is stronger than EC, which is stronger than E². The properties for the three filter types are summarized in Table 2.

3. Application

In practice, the data set is not filtered in one piece, but rather “tiled” into overlapping blocks in both time and space, just as one would do for f-x prediction (Canales, 1984). These tiles are noise suppressed separately and then recombined into a single data set by tapering and summing. Such a scheme makes these filters local in both time and space, limiting the number of conflicting dips that need be handled simultaneously.

The strength of each filter is controlled by the tile size and the rank; the smaller the rank or the larger the tile size, the harsher the filter. A single tile typically has a spatial window length of 15 to 25 traces in each dimension and a time window length of 300 to 600 ms. The exactness property says that we can expect signal loss when the number of conflicting dips exceeds the rank; hence the maximum number of distinct dips in a tile is a lower bound for the rank that is safe to use.

Data Preparation

In preparing seismic data, trace-equalization, deconvolution, and statics should be applied if Cadzow is being used. We prefer the data to be NMO corrected, although perfect velocities are not required since these filters can handle slightly under- or over-corrected events. The goal of NMO correction is to reduce the number of conflicting dips. This allows a lower rank to be used, yielding stronger noise attenuation. If the data contains very strong coherent noise then it should be attenuated before these filters are applied. Recall that a rank-k filter will preserve the k most energetic dips. If a low rank is used and the data contains strong coherent noise, then the filter may preserve this noise and lose the weaker signal.

Filtering Domains

A critical step in rank-reduction-based filtering is deciding what the spatial dimensions will represent. Two common domains are shot-receiver and CMP-offset. The shot-receiver domain is often used for noise suppression prior to prestack migration. The main obstacle is that shot spacing is often non-uniform, but this can be handled by treating the shot dimension as eigenimage within a hybrid filter. The CMP-offset domain is often used after prestack migration. The uniformity of the CMP and offset-bin spacing makes this domain ideal for pure Cadzow.

Source-Receiver Domain

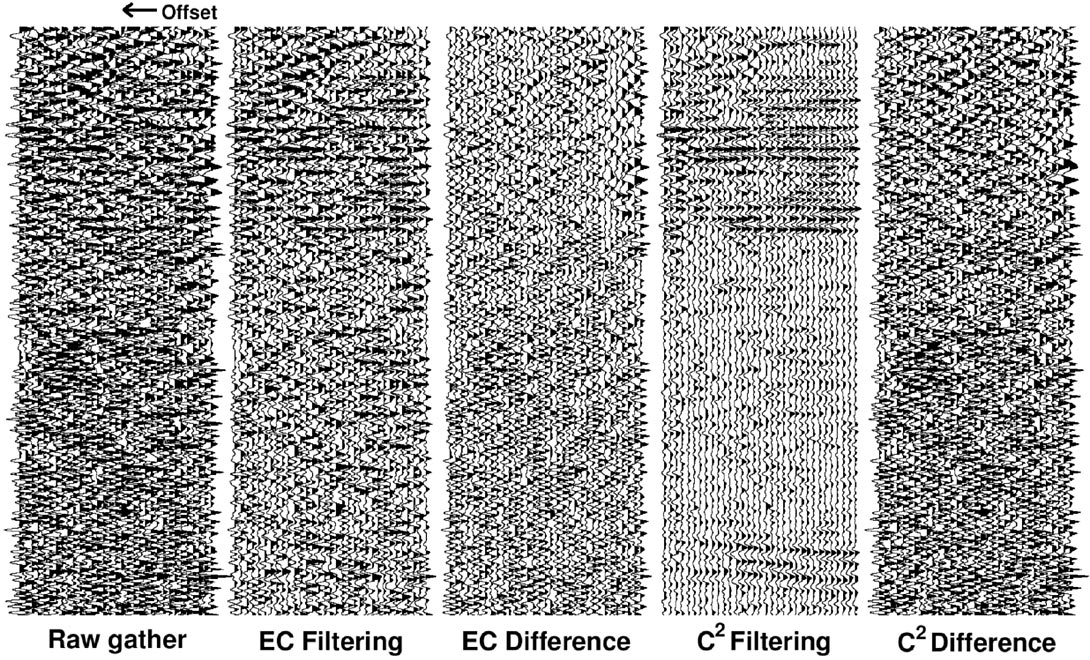
A powerful way to perform prestack noise suppression is f-xy filtering with the spatial dimensions representing source and receiver (Grimm et al, 2003). For land data, receivers are typically uniformly spaced but sources are not. This suggests using eigenimage- Cadzow (EC) filtering, where the source points are treated as eigenimage and the receivers are treated as Cadzow. This filter is of moderate strength, and can handle source-consistent (but not receiver-consistent) statics. For severe noise problems we can use a pure f-xy Cadzow (C²) filter. If sources are not uniformly spaced, however, we may be smearing structure for the sake of better signal-to-noise.

Figure 5 shows the results of shot-receiver-domain application of EC and C² filtering on a noisy structured 2-D line. The stacked sections are in Figures 6 through 8.

For 3-D volumes we can divide the data into cross-spreads (Vermeer, 1988) – that is, we take every combination of receiver line and source line, and filter each combination separately as we would a prestack 2-D line.

A second option for 3-D data is to work with multi-cross-spreads which group together all of the traces from a single source line and multiple receiver lines. Bouska (2009) called these 3-D shot salvos. Each multi-cross-spread is filtered using an EC² filter, where the dimensions are source position, receiver line and receiver position, treating the source dimension as eigenimage. This filter is very strong, and is appropriate only for noisy data sets where we are “desperately seeking signal”.

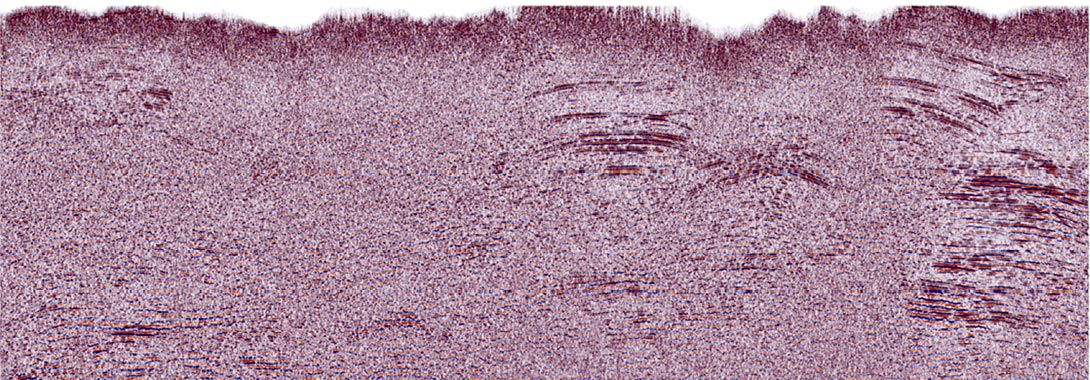
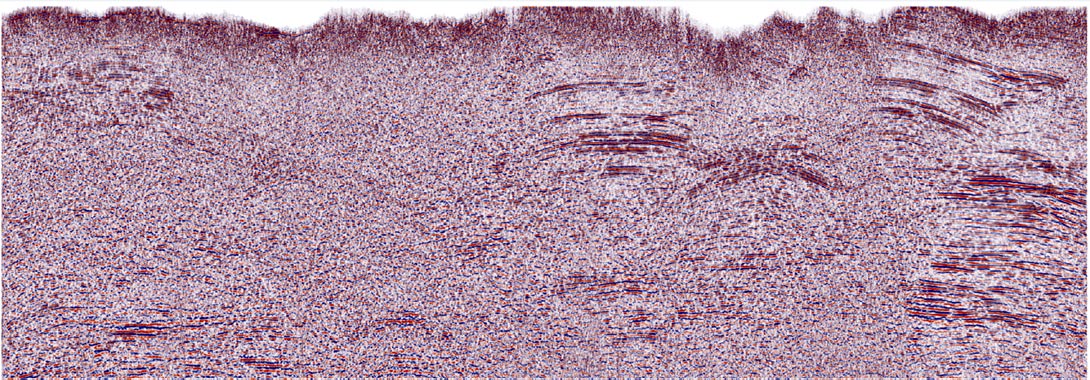
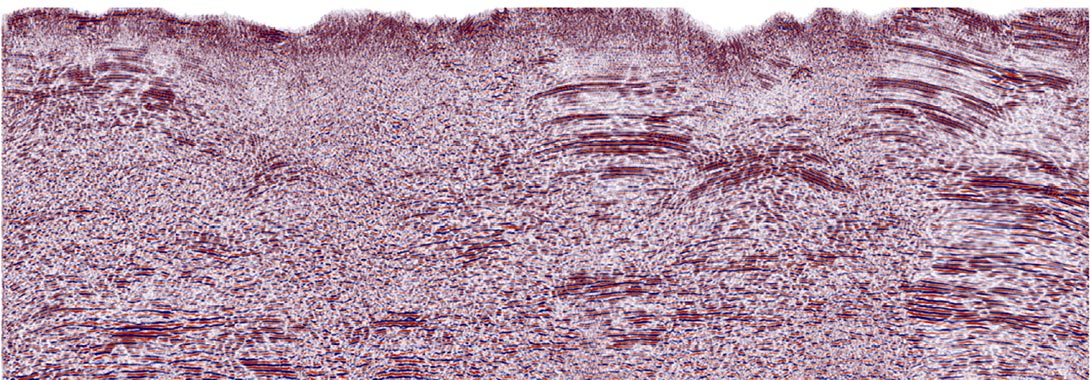
CMP – Offset Domain

In the CMP-offset domain, the uniform spacing and density of the CMP grid is ideal for Cadzow filtering. The principal problem is that offsets are erratically spaced in each gather. Two solutions are to (1) bin the offsets to create common-offset stacks beforehand, or (2) perform prestack migration beforehand. Solution 1 is a good option if the only goal is to produce a clean stack, perhaps one to be used as a model for statics analysis. Solution 2 – performing noise suppression after prestack migration – is more useful.

For 2-D data, one can apply either a pure Cadzow C² filter (Figure 9) or a hybrid EC filter where the offset dimension is treated as eigenimage. The latter is safest when the offset bins are not equally spaced.

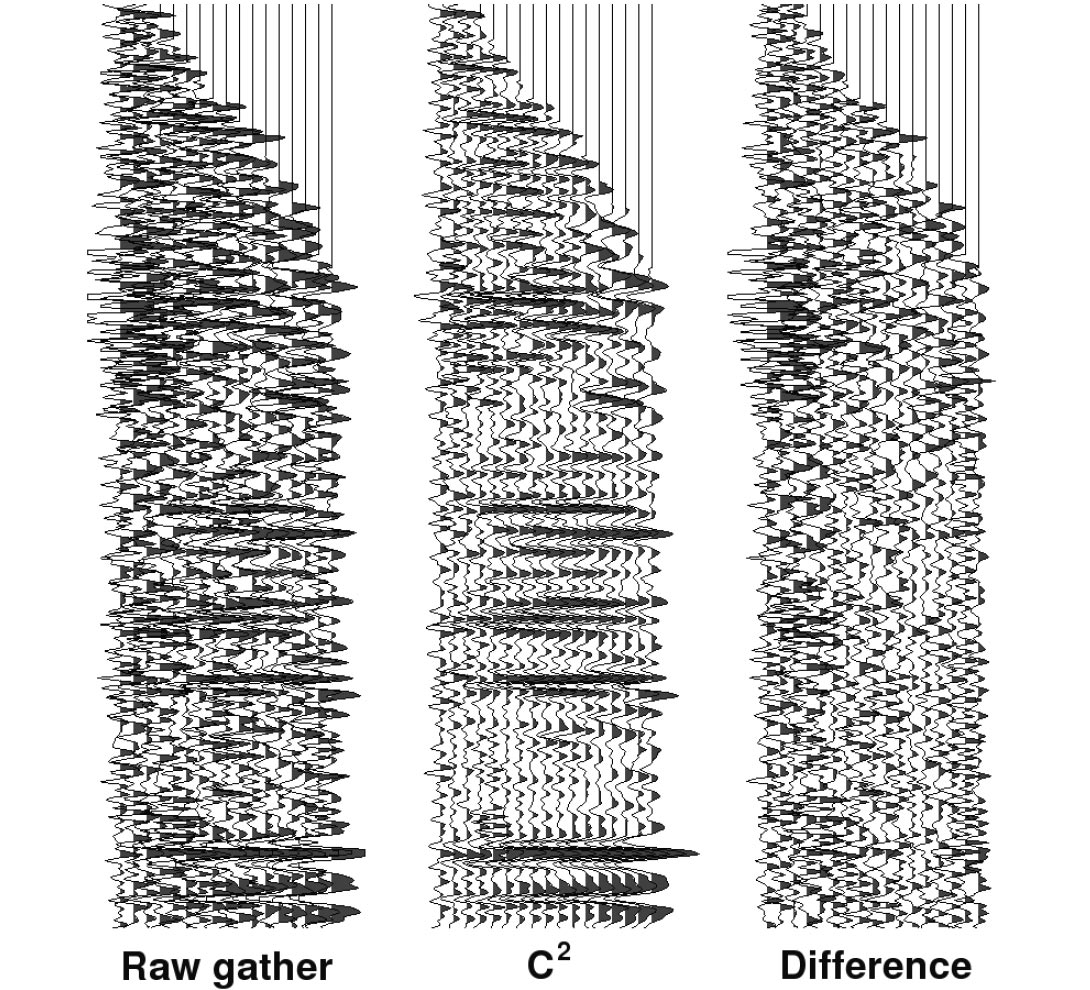
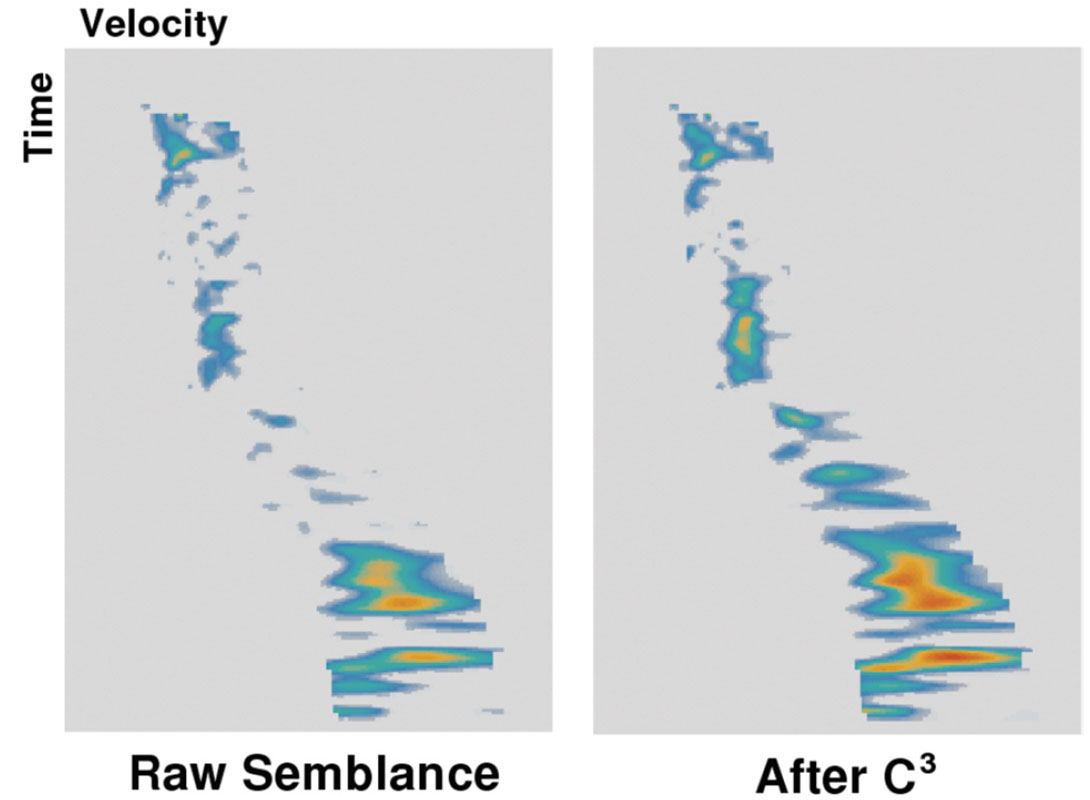
For 3-D data, one can apply an EC² or C³ filter. Since Cadzow filtering becomes about four times stronger (that is, increases the signal-to-noise ratio by four) with each added dimension, the C³ filter is extraordinarily powerful at revealing signal in very noisy areas (Figures 10 and 11). Prestack noise suppression can also enable more accurate velocity analysis (Figure 12).

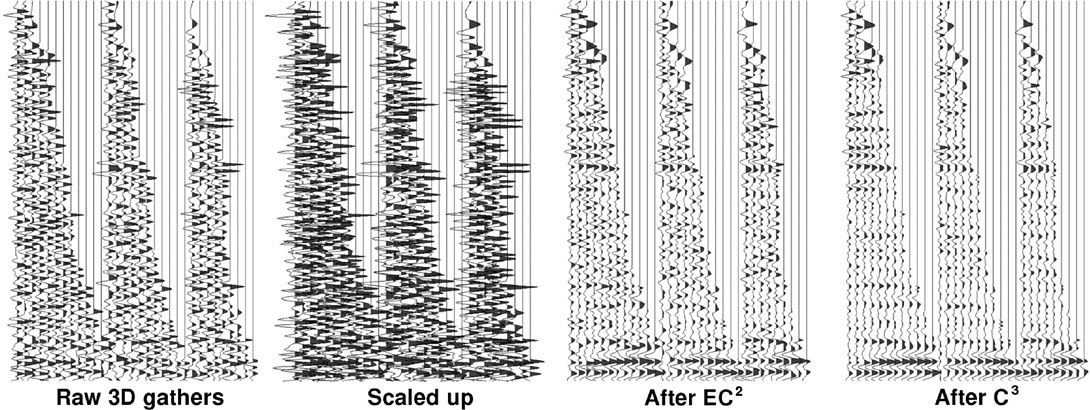
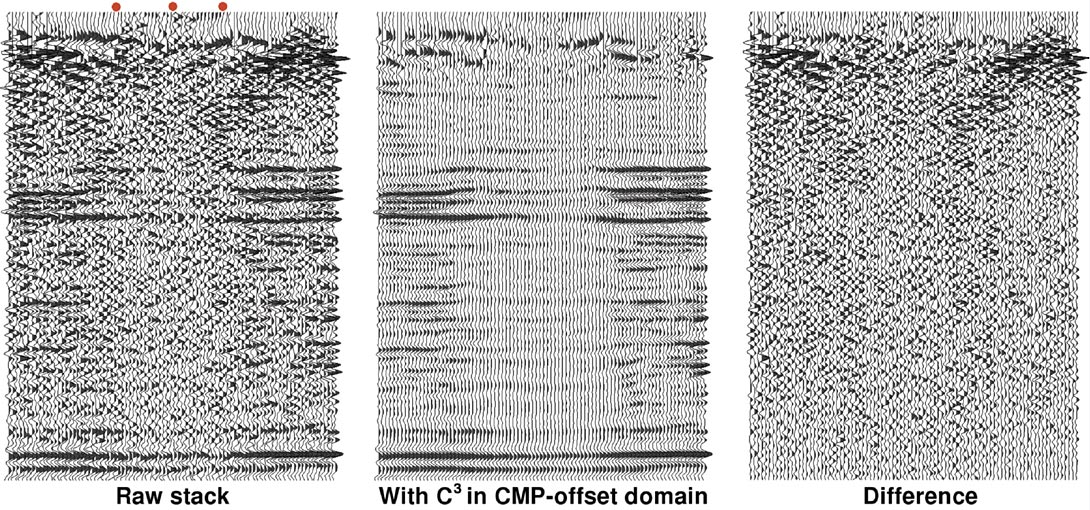
4. AVO, AVAZ, Timelapse, and Artifacts

Rank-reduction-based filters preserve AVO effects, as our examples have shown and the following property indicates:

AVO Property: Suppose we have a d-dimensional grid of traces containing s linear events without noise. These events may each have distinct dips in d-1 dimensions. However in one of the dimensions, termed the offset dimension, each event i is flat except that its amplitude varies as a function pi(h), where h is offset trace number and pi(·) is a polynomial of degree q_i.

Then the d-dimensional rank-reducing filters described above do nothing to the data provided the offset dimension is treated as

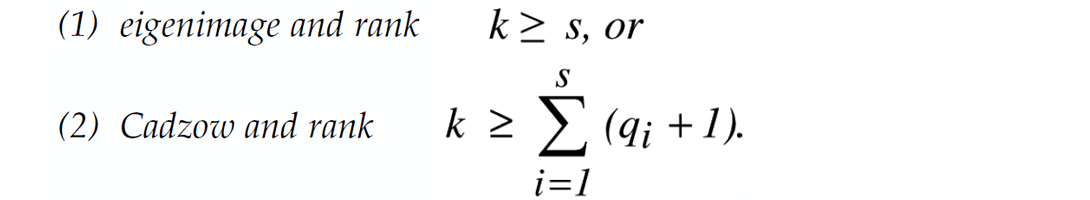
This rather imposing property means that these filters can handle AVO effects provided the rank is not set too low. To be safe, the offset dimension should be treated as eigenimage, although in practice we haven’t found this to be necessary when offsets are evenly spaced.

Figure 13 shows an artificial 3-D prestack volume. The data set contains three events dipping in the CMP direction, although we show only a single gather. Notice the AVO effects. Noise was added to the entire data set, making AVO analysis nearimpossible. We applied C filtering separately to each offset plane, first in the inline direction, then the crossline direction. AVO analysis of this would be pretty dodgy. We then tried C² filtering on each offset plane separately. Although better, it is questionable whether we can perform AVO analysis on the middle event. Finally we applied C³ to the entire noisy data set as a whole. AVO analysis would now not be a problem, as we have closely reproduced the original clean input.

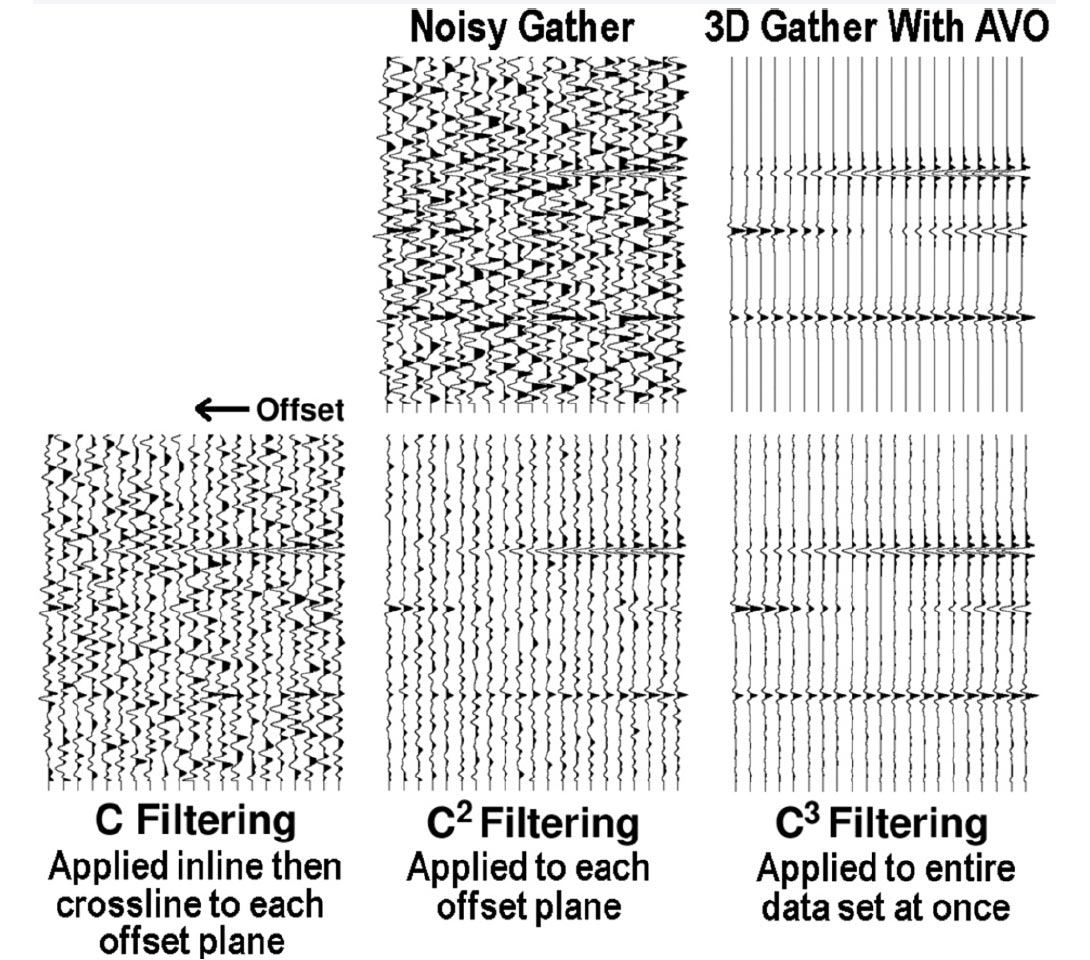
There are two conclusions from this test:

• These methods are AVO friendly.
• More spatial dimensions equal more power. It is a huge benefit to filter in as many spatial dimensions simultaneously as possible.

Thus rank-reduction-based filters might allow AVO exploration in regions where it was not possible before due to noise. The filters are also AVAZ friendly:

AVAZ Property: Suppose we have a d-dimensional grid of traces containing s linear events without noise. These events may each have distinct dips in all dimensions. However, in one of the dimensions, termed the azimuth dimension, each event i is convolved with a wavelet f_i(z), where z is azimuth trace number. Then the d-dimensional rankreducing filters described above do nothing to the data provided the azimuth dimension is treated as eigenimage and rank k ≥ s.

In other words, rank-reduction-based filters can handle AVAZ effects provided the azimuth dimension is treated as eigenimage and the rank isn’t set too low. The azimuth dimension should never be treated as Cadzow. This dimension is unusual in that it wraps around; 0 degrees is the same as 360 degrees. Cadzow cannot model this but eigenimage can.

Timelapse Processing

Timelapse (often called 4-D) data is seismic data that has been repeatedly reshot over many months or years for the purpose of detecting changes in reservoir properties. The AVAZ property above suggests an intriguing possibility for noise suppressing all vintages of the timelapse simultaneously – apply a hybrid filter where the vintage dimension is treated as eigenimage. Eigenimage allows for bulk shifts and differences in time-domain filtering between vintages, and should preserve timelapse effects. Eigenimage also avoids assumptions about the “distance” between vintages. EC³ filtering in the vintage-CMP-offset domain would give extraordinarily strong noise suppression.

Resistance to Artifacts

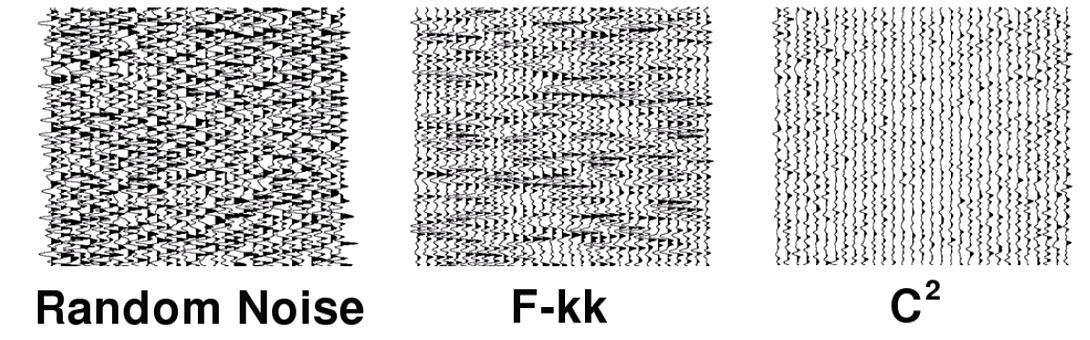
At a recent CSEG technical luncheon, Bouska (2009) referred to fk- type filters as “evil” for their tendency to generate artifacts. A good test for any noise-attenuation filter is to apply it to pure random noise and examine the output for coherency. An f-kk filter generates coherent artifacts that could easily be mistaken for signal, a problem that also plagues other dip filters such as the conventional linear radon transform. In contrast, rank-reduction- based filters reduce noise without generating artifacts that could be misinterpreted as seismic events (Figure 14).

5. Final Remarks

We have described a powerful and versatile family of randomnoise- suppression filters and demonstrated many ways that they can be applied to prestack data.

In the introduction we listed nine properties that an ideal prestack random-noise suppressor should have. This new family of noise suppressors substantially meets these criteria. One weakness is that we must often trade off filter strength for other properties such as the ability to handle non-uniform spacing. Future improvements may overcome this.

The three-spatial-dimension versions of these filters are so strong that they have the potential to reveal previously hidden signal, perhaps opening up areas that were once unexplorable with the seismic method. They may also allow AVO analysis in areas that were previously too noisy.

Acknowledgements

Thanks to Pulse Data, Compton Petroleum, and Husky Oil Operations Limited (in particular David Emery and Larry Mewhort) for permission to show their data. Also thanks to Mike Jefferd, Ruth Peach and the rest of the staff at Kelman Technologies for their invaluable help.

This research was partially funded by the National Research Council of Canada.