What Comes Up Must Have Gone Down the Principle and Application of Up-Down Deconvolution for Multiple Attenuation of Ocean Bottom Data

Abstract

Up-down deconvolution is a method for attenuating all free surface multiples from ocean bottom seismic data, by exploiting the separation into up and down-going wavefields from combining hydrophone and geophone data. We describe the method and show its application both to a synthetic dataset provided to us by Chevron and to a field dataset from the Norwegian sector of the North Sea, comparing it to the more conventional approach of PZ summation. An additional benefit of the method for 4-C acquisition is that free surface multiples on the PS data can also be suppressed by deconvolution of the horizontal components with the same down-going wavefield.

Introduction

Ocean bottom recording (Figure 1) is a small but important segment of the marine seismic acquisition market. There are two main types of ocean bottom recording: ocean bottom cable (OBC) in which a cable containing multicomponent sensors is deployed from a boat using an umbilical connection and with typical inline receiver spacing similar to that of towed streamer; and ocean bottom seismometer or node (OBS or OBN) in which a number of multicomponent nodes are deployed individually, usually by a remote operated vehicle (ROV) and with a typical receiver spacing of 100- 400m. OBS acquisition tends to be preferred for very deep water surveys where cost of cable deployment becomes prohibitive and also in the presence of seabottom obstructions, like pipelines and platforms. In both OBC and OBS acquisition most modern systems make use of four component (4-C) sensors, consisting of a 3-C geophone and a hydrophone. This allows recording of the full elastic wavefield. Hydrophone and geophone respond differently to upand down-travelling waves.

Reasons for acquiring OBC or OBS data include the presence of obstructions, which would make streamer acquisition impossible, wide azimuth illumination, the ability to also record shear-wave data, a quieter recording environment, and higher resolution. Higher resolution is possible because there is no longer a conventional receiver ghost. In fact the “ghost” is now coincident in time with the first order water layer multiple energy. This might at first sight seem a step in the wrong direction. However, because both vertical geophones and hydrophones are collocated in 4-C receivers, and record the ghost with opposite polarity, the ghost can be attenuated effectively by a weighted combination of the two.

The polarity difference arises from the difference between a scalar measurement (pressure) and a vector measurement (displacement/velocity/acceleration). The pressure measured by the hydrophone is not dependent on the direction in which the wave is travelling, whereas the velocity measured by the geophone is. So if the up-going wave is assumed to have the same polarity on both, this implies opposite polarities for the down-going waves (Figure 2).

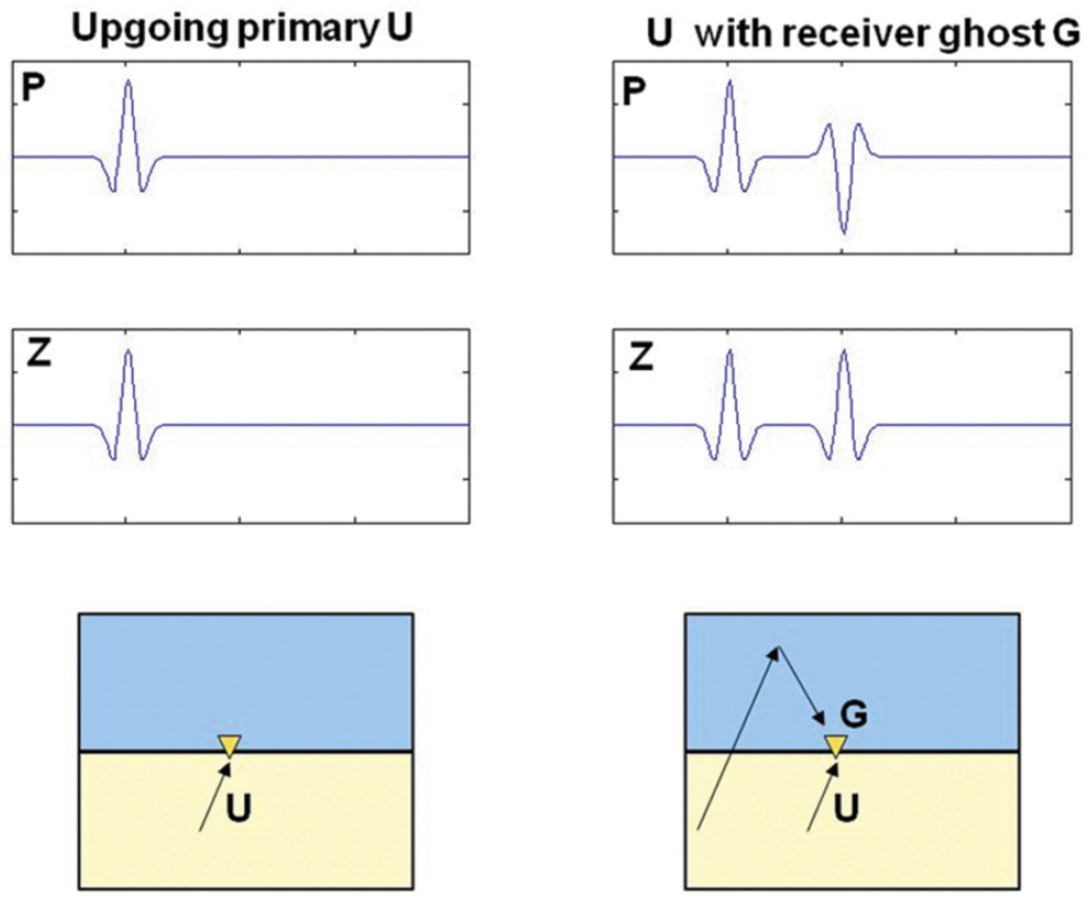
Conventional PZ summation (Barr and Sanders, 1989; Soubaras, 1996; Schalkwijk et al., 1999; Osen et al., 1999) can be used to attenuate all multiple energy which is down-going at the receiver location. By appropriate scaling of the vertical geophone (depending on seabed reflection coefficient) it can also include attenuation of the multiple which is generated from the downgoing wave by the seabed. An equivalent way to express this is to regard the up-down separation as taking place infinitesimally under the seabed – so that this multiple is absent. In Figure 3 there are two contributions to U_above, one from the earth (right side) and one from the seabed bounce (left side). However, if we conduct the PZ summation at a location just below the seabed, then we estimate U_below, which eliminates the seabed bounce.

For the simple case of vertical propagating waves, the equation which describes summation above the seabed is simply

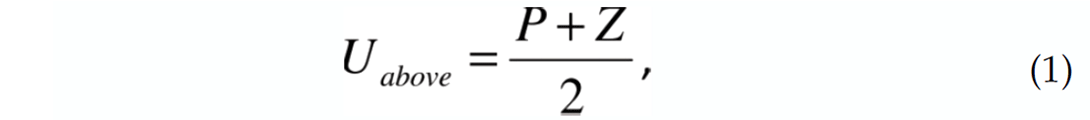
where P and Z are the hydrophone and vertical geophone recordings respectively, and U is the estimated up-going wavefield. In equation (1) and in the following derivation Z is scaled by the water impedance ρc, where ρ is the water density and c the water velocity in proximity of the sensor. For summation below the seabed the corresponding equation is

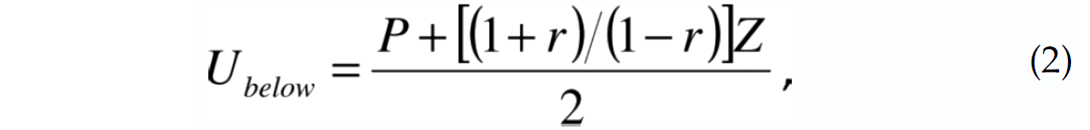
where the term in square brackets involving the seabed reflection coefficient, r, is designed to account for the bounce off the seabed at the receiver. It can be also shown that this term corresponds to a change of impedance from the water layer to the seabed medium.

For non-vertical arrivals these two equations are modified to account for different arrival angles as described in Bale (1998).

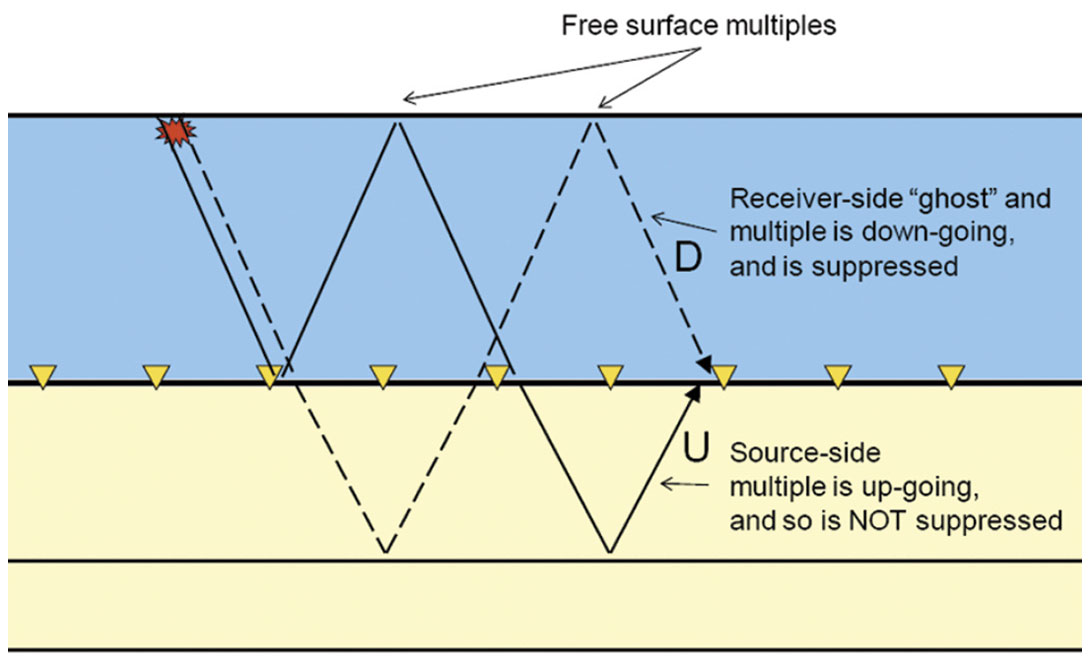
The PZ summation strategy we have just described allows for effective attenuation of “receiver side” multiple energy (multiples which have their free surface reflection just before recording). However, there are other multiples, such as “source side” multiples, which are not down-going at the receiver and are not attenuated by conventional PZ summation. This is illustrated in Figure 4. In order to attack these multiples we need to go a step beyond conventional PZ summation. We need to do updown deconvolution instead.

The up-down deconvolution method

The theory of using up-down deconvolution to address free surface multiples in a layered media has been known for a long time (see, for example, Sonneland and Berg, 1987). Amundsen (2001) discusses the method in detail and extends the method to more complex geology. The enterprising reader is referred to this paper for detailed explanation of the mathematical basis. Here we offer an explanation based on intuitive physical reasoning.

In fact, the title of this paper actually describes the fundamental principle of up-down deconvolution: what comes up must have gone down. Our source wavefield is generated near the ocean surface (the free surface). Everything we record at the receivers is the result of something which originally went downward from the source and from various bounces off the free surface, and has also been recorded by those same receivers. But it has been modified by the very thing we seek information on: the earth’s reflectivity. Figure 5 illustrates for a simple ray-path how we can represent a recorded up-going signal as the combination of a down-going signal with the response of the subsurface.

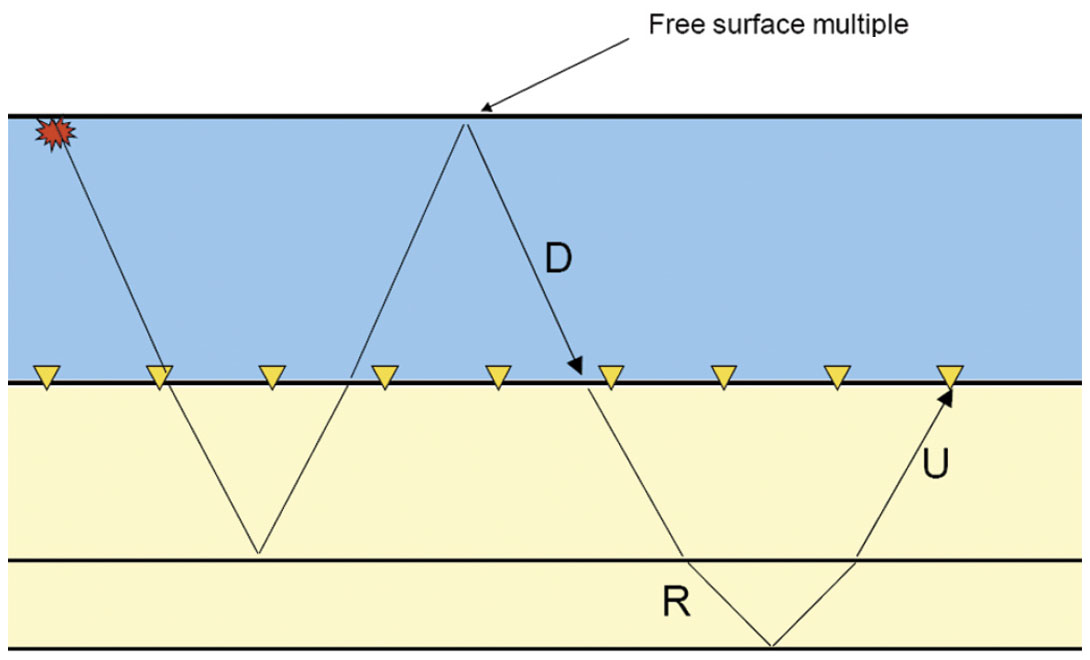
Though illustrated for a single ray-path, this concept is applicable to the wavefield as a whole. For a simple layered medium, the addition of travel times implied by combining these two ray-paths is represented by a convolution for a common ray-parameter, or in the FK domain as a multiplication. So we have a simple equation:

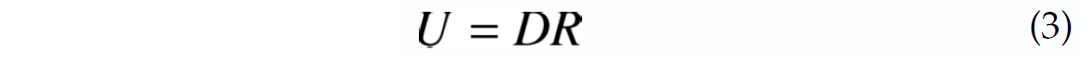
Where U is the measured up-going wavefield, R is the earth’s reflectivity and D is the down-going wavefield, all expressed in the F-K domain (or F-K_x-K_y for 3-D). This is very easily inverted, using a stabilization factor ε to prevent noise resulting from spectral notches, to get an estimate of the earth reflectivity.

Of course in order to apply equation (4), we first need to estimate the up-going and down-going wavefields. This is done using the PZ summation above the seabed which is described in the previous section. The success of the method largely hinges on how well it is possible to achieve this separation.

It is important to note that the up-down deconvolution method is applicable not only to the pressure and vertical component recordings but also to the horizontal components and therefore allows a complete free-surface demultiple for convertedwave (PS) data – something difficult to achieve using other methods. For example, velocity based discrimination of multiples and PS primaries is problematic because multiples are often faster or have a similar speed to these primaries.

Synthetic example

We apply up-down deconvolution to a 2D 3C isotropic finite-difference synthetic dataset provided by Chevron. The dataset consists of 170 OBS nodes at a depth of about 1375-1837m and 1280 shots at a depth of 12.5m. Shot and receiver sampling is 12.5m and 100m, respectively. The sea bottom is gently flat with an average dip of 1.6 degrees but significant subsurface structure is present (Figure 6).

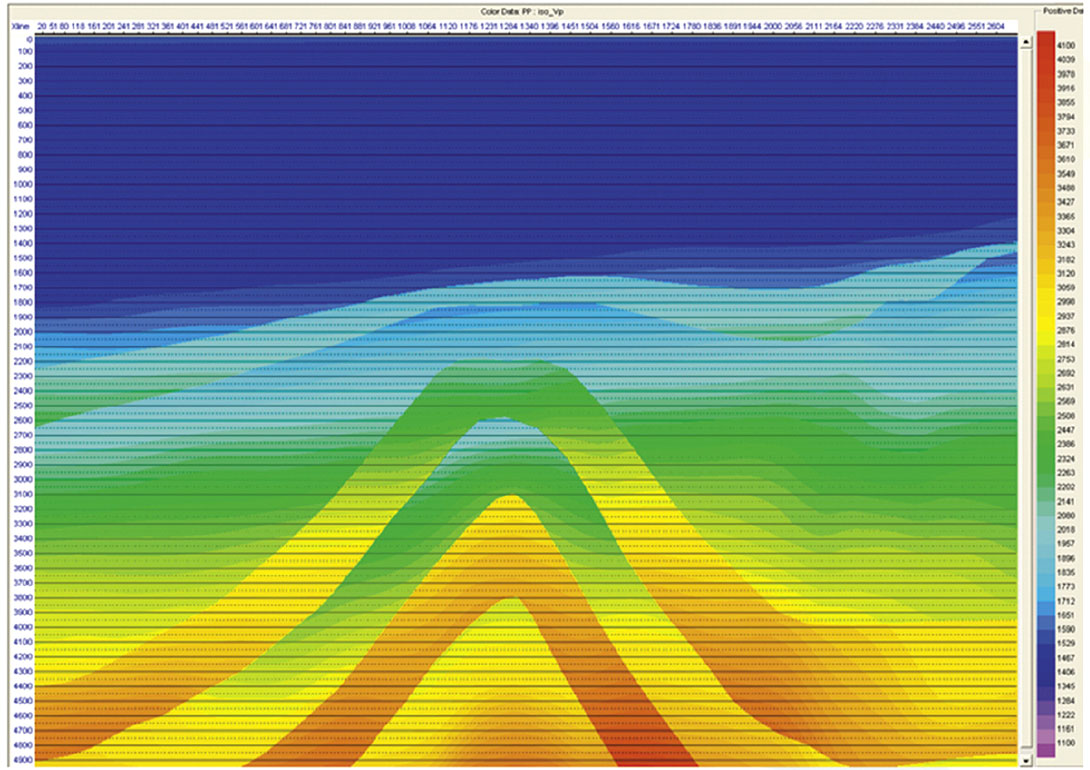
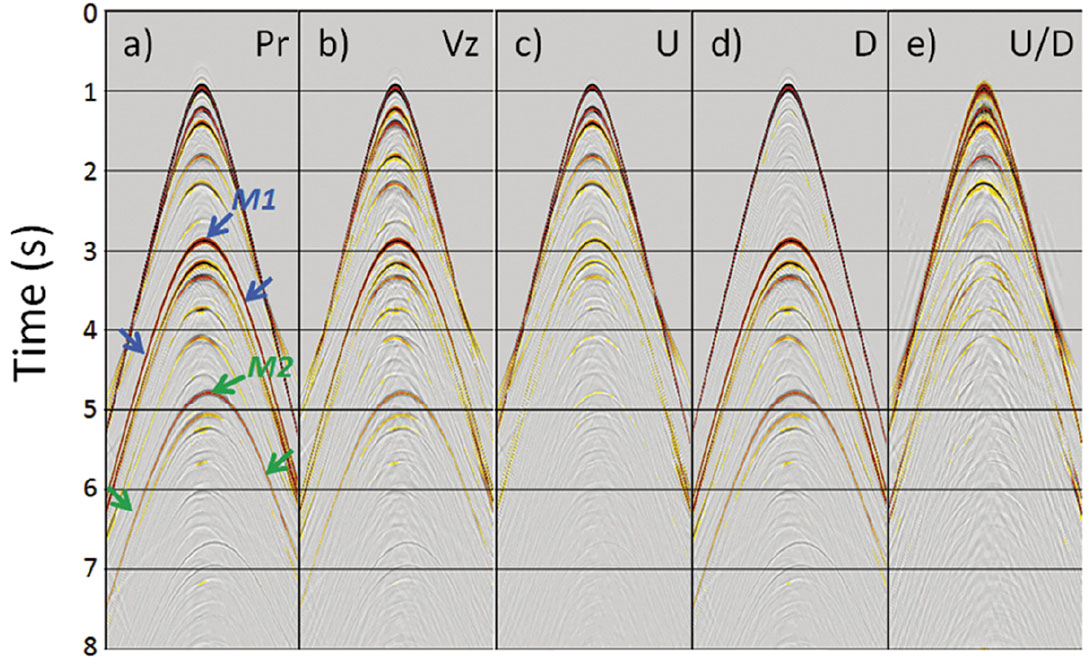
The synthetic data have a zerophase wavelet with 50Hz bandwidth, therefore aliased energy (at about 60Hz) is well beyond the bandwidth of interest. In our processing flow, we choose to calibrate the vertical velocity component Z against the pressure component P using the cross-ghosting method (Soubaras, 1996). After P and Z components (Figure 7a and 7b) are calibrated, we separate upand down-going waves just above seabed in the f-k domain (Figure 7c and 7d). Then we deconvolve the downgoing waves from the up-going waves for each receiver. The up-down deconvolution result clearly shows that all free surface related multiples are successfully and completely removed (Figure 7e). As an example, note the removal of multiples M1 and M2. For comparison purposes, we also process the data using a conventional PZ demultiple approach. The data after these different processing routes are then migrated using a prestack depth Kirchhoff algorithm adapted for OBS geometry. Compared to the original Z or P component migrations (Figures 8a and 8b), conventional PZ demultiple shows considerable attenuation of the multiples, but residual shot-side multiples are clearly present (Figure 8c). The up-down deconvolution result (Figure 8d) delivers improved multiple attenuation with respect to the conventional PZ summation, especially in the reservoir area. Migrated stack sections confirm the efficacy of the multiple remove process.

Field data example

As a second example, we apply the updown deconvolution to PP and PS data of a receiver gather from a 2D4C OBS dataset recorded offshore Norway on the headwall of the Storegga Slide (Figure 9). Migrated images and an introduction to the geological setting of this dataset are discussed in Grion et al. (2007). Storegga, or “great edge” in Norwegian, is the largest known submarine slide, involving the collapse of an area of continental shelf about the size of Ireland. It is located 100km offshore Norway above the giant Ormen Lange gas field. The survey targets here are shallow sediments containing gas hydrates.

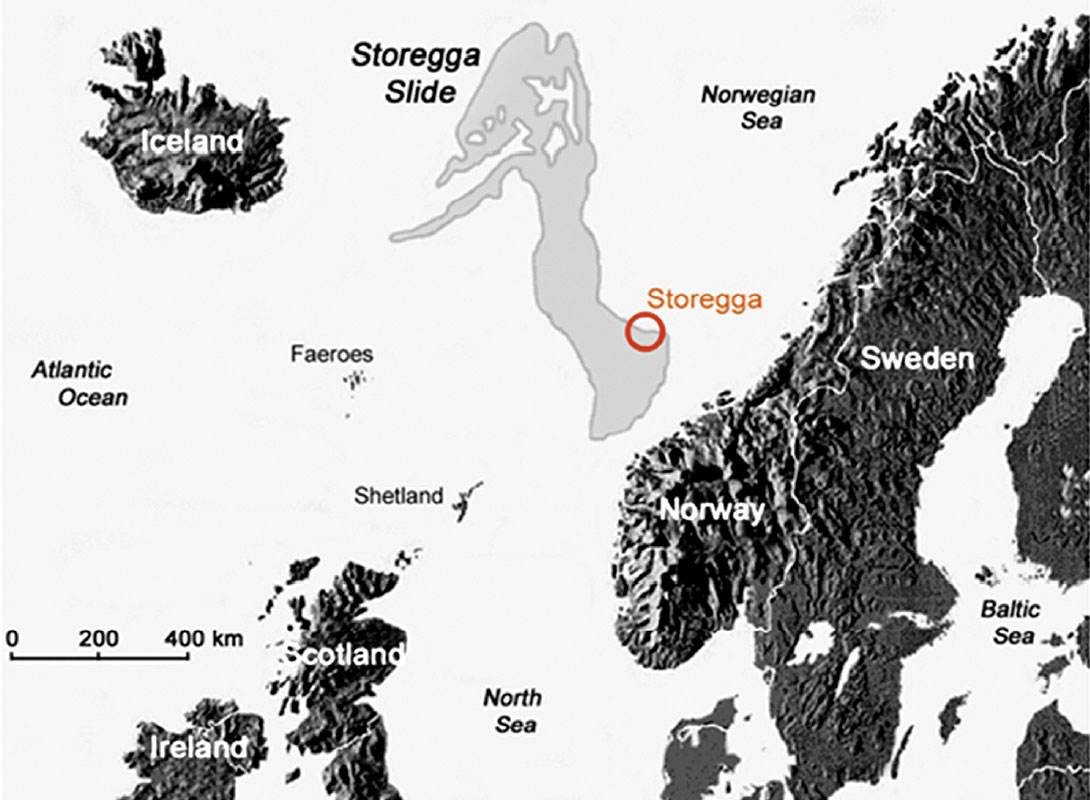
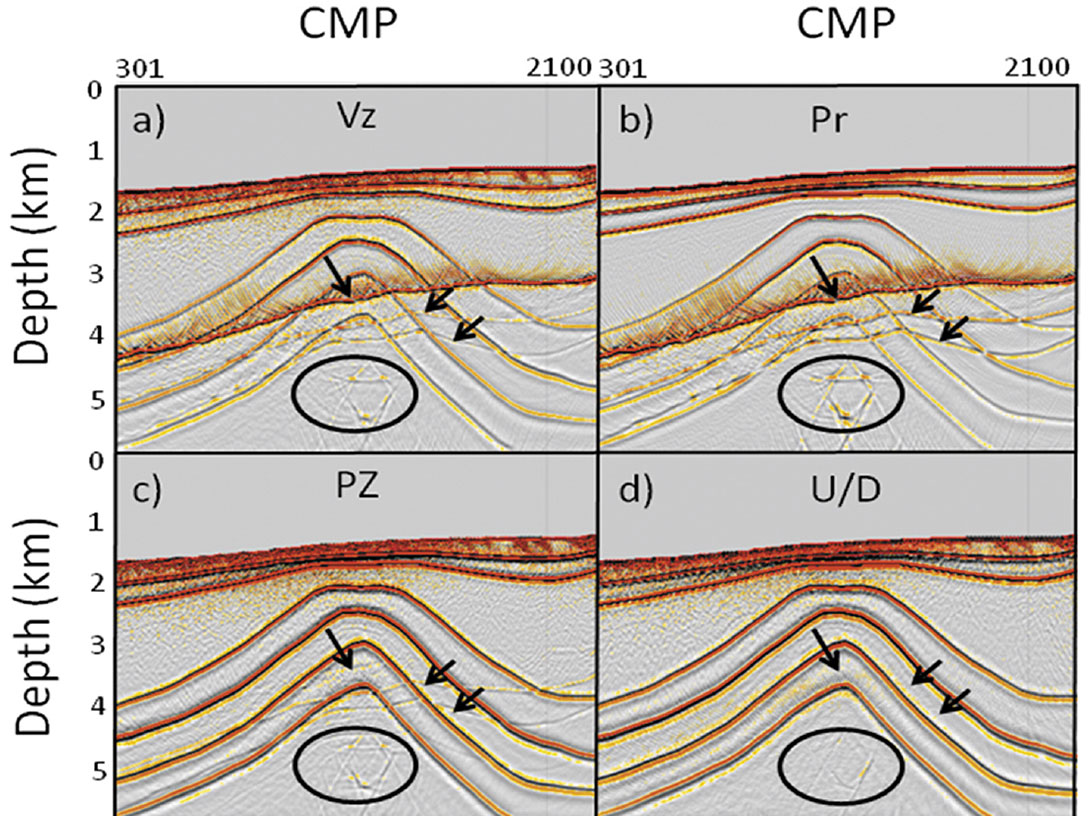
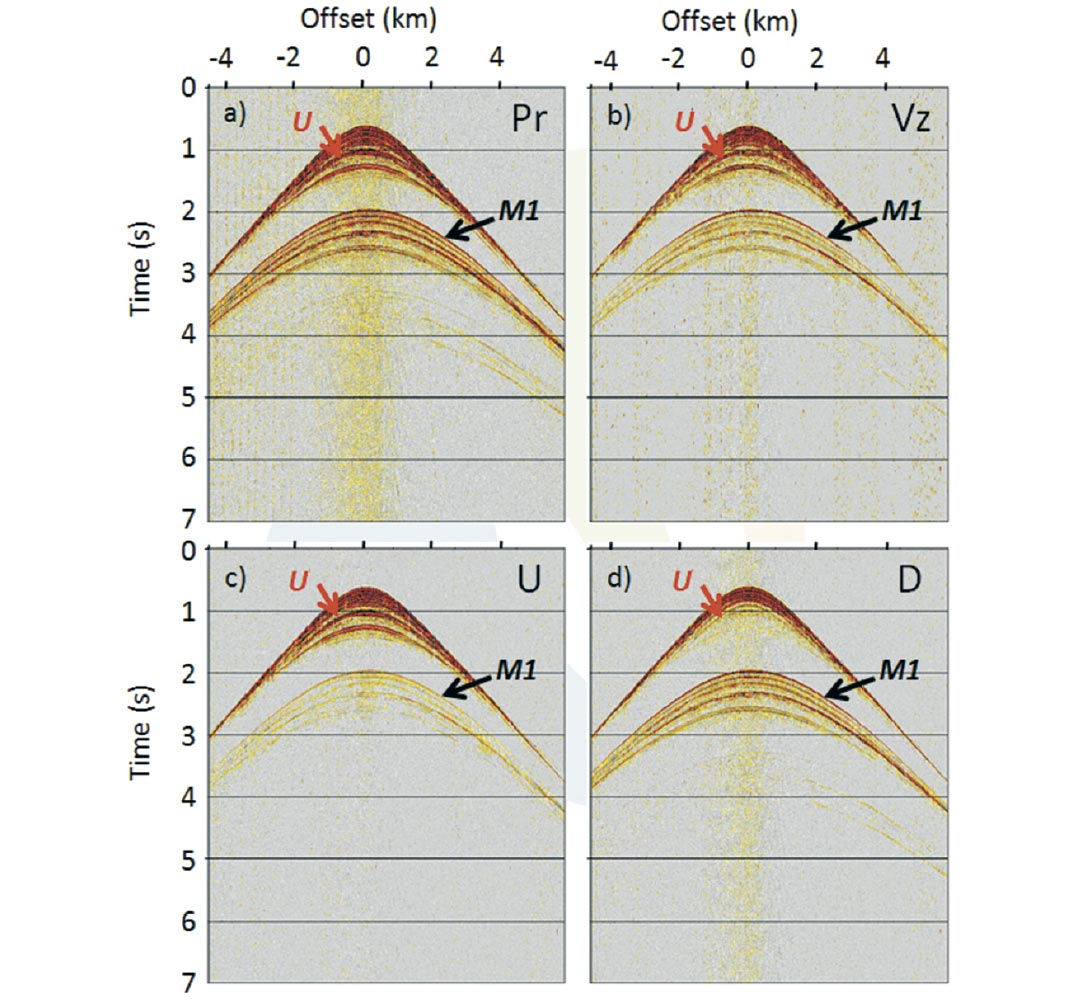
Figure 10 shows a common receiver gather for the pressure and vertical component and the corresponding upand down-going waves calculated using equation (1). We apply a conventional demultiple approach and our proposed up/down deconvolution approach to the PP data of this receiver gather. The result shows shot-side surface-related multiples cannot be eliminated by the conventional demultiple approach, but they can be removed by the up-down deconvolution approach (Figures 11a and 11b). We also apply a similar approach to the radial component. Our result indicates the surface-related multiples can also be removed for the PS data (Figures 11c and 11d).

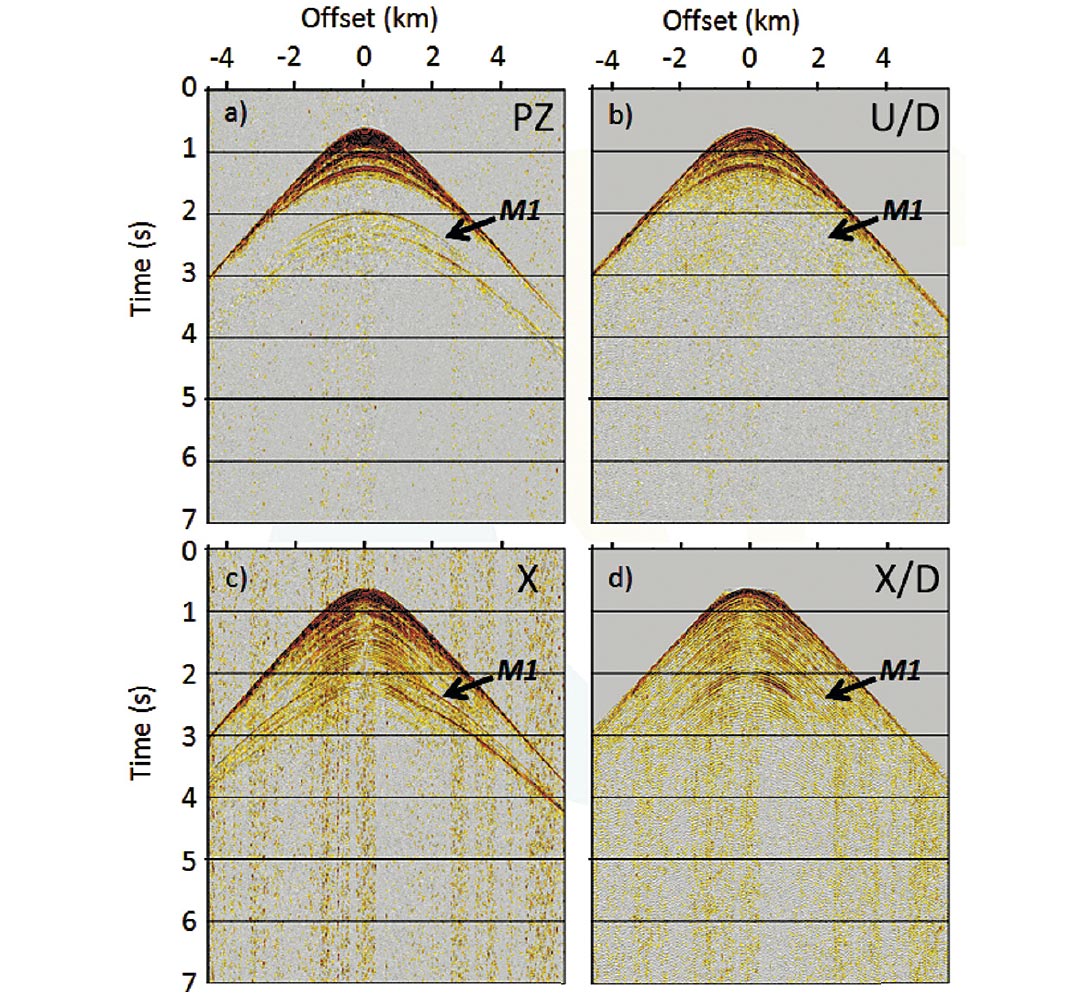
Discussion

The up-down deconvolution method for free-surface demultiple is certainly not new but its application is gaining momentum for a number of reasons. Firstly, continuous improvement in data acquisition and processing allow better separation of the pressure wavefield into its up-going and down-going parts, a critical step for the success of this method. Secondly, unlike conventional PZ summation (equation 2), up-down deconvolution does not require any knowledge of seabottom properties, it removes both source-side and receiverside multiples and can also be applied to the horizontal components. Last but not least, because the source signature and its associated directivity effects are contained in both the up-going and down-going wavefields, up-down deconvolution also acts as a very effective and automatic directional designature algorithm, as noted by Amundsen (2001).

It is important to note that accurate 2D and 3D application of the method may require data interpolation and regularization. In particular, missing near offsets have a detrimental effect and must be interpolated before the method can be applied. Furthermore, accurate separation of the direct arrival into its up-going and down-going components is fundamental to the success of updown deconvolution, especially at near offsets.

Conclusions

Up-down deconvolution is an effective and automatic free-surface demultiple method for ocean-bottom data. Its application requires accurate separation of the recorded pressure wavefield into its upgoing and down-going components. The synthetic example shown highlights the success of the method even in presence of complex geology, albeit with a relatively flat seabottom. The method is strictly valid for a horizontally-layered earth but is remarkably robust for scenarios such as the one shown.

Acknowledgements

The Storegga data is courtesy of the European Commission funded HYDRATECH project EVK3-CT-2000-00043, processing was carried out at CGGVeritas. We are grateful to Chevron for generation of the synthetic data used in this paper and for permission to publish the results. We thank Steve Roche, Terence Krishnasamy, Kevin Douglas and Linping Dong for their contributions in imaging the synthetic data.