Neural network analysis and impedance inversion – Case study

Summary

Inversion of post-stack seismic data is routinely done to obtain information about the P-wave impedance, which provides reliable information about the reservoir lithological properties. The most commonly used method for estimating P-impedance from the seismic traces is the model based inversion. This method requires an initial model and a wavelet estimated from seismic data. The model is recursively updated till the data misfit falls below a user defined value. The final updated model is the accepted P-impedance volume. Another method that has been discussed in the literature is the neural network based impedance estimation using Probabilistic Neural Networks (PNN). A conjugate gradient algorithm is used to train and validate the PNN for estimation of density and velocity separately, using an optimum set of attributes. P-impedance is then computed from the estimated density and velocity. Our objective here is to show a comparison between these two methods, namely the model-based impedance inversion and the neural network based impedance estimation. We demonstrate this comparison on a 3D seismic volume from Alberta, Canada. Our results show reasonable qualitative comparison, with the PNN estimated impedance showing better correlation with impedance logs.

Introduction

P-impedance is a useful parameter for seismic interpreters as it provides more accurate and reliable information about the lithological properties of the reservoir. Conventionally, Pimpedance is obtained from the seismic data via model-based inversion which requires an initial model and an estimation of wavelet.

Neural networks have been in use for geophysical applications since the early 1990s. McCormack (1991) described some of the early geophysical applications of neural network by predicting lithology log for an entire well using backpropagation Multi-Layer Feed Forward Network (MLFN). Subsequent to this work, Schultz et al. (1994) proposed the application of neural network in estimating the log properties from the seismic data in a data-driven interpretation framework. Liu and Liu (1998) applied the neural networks for the inversion of sonic and shale content logs using well-log and seismic data. Dorrington and Link (2004) describe an approach based on combination of genetic algorithm and neural network to predict the porosity log for a 3D data. The hybrid strategy is used to determine the optimal number and type of attributes that can accurately predict the porosity in the reservoir zone. Recently Shahraeeni and Curtis (2011) have developed a probabilistic neural network strategy to invert for the reservoir petrophysical parameters (porosity, clay content etc.) from the elastic properties of the reservoir.

We have used the Probabilistic Neural Network (PNN) in a case study for estimating the P-impedance from the seismic data and available well-logs. Our approach is based on training and validating a PNN network for predicting the density and the sonic log over a 3D volume. The attributes selected as input to the PNN nodes are obtained from a linear multi-attribute regression analysis. We have used the convolutional approach (Hampson et al., 2001) in the regression analysis so that the well-logs and the seismic data are properly scaled in terms of their frequency contents.

The selected attributes obtained from the linear regression analysis is used in a PNN framework for training and validating the network using the available well-logs. Once the network is adequately trained and properly validated, the prediction of the target logs (e.g. density and P-wave velocity) over the entire 3D volume is carried out.

Method

The P-impedance is estimated in two different approaches namely, (a) model based conventional inversion and (b) probabilistic neural network based estimation of P-impedance via individual estimation of density and P-wave velocity.

Model-based inversion requires an initial model and estimation of a wavelet from the data. The initial model of P-impedance is generally obtained from the available well logs by interpolation and application of a low pass filter (~10 Hz). The wavelet is estimated from the data. The reflectivity is computed from the impedance model and subsequently convolved with the estimated wavelet to compute a seismic trace. The estimated trace is used to compute the data misfit based on the L₂-norm. The impedance model is iteratively updated and data misfit is minimized till an acceptable misfit error is achieved. The final updated model is the accepted Pimpedance for the zone of interest. The shortcoming of this method is that the solution is largely affected by the nonuniqueness of the problem which in turn makes the solution dependent on the chosen initial model.

Neural network based estimation is based on two important neural network architectures- (a) Multi-Layer Feed-forward Neural Network (MLFN) and (b) Probabilistic Neural Network (PNN). The MLFN network consists of an input layer, one or more hidden layers and an output layer. Except the output layer, all other layers have more than one node. Each node is associated with a weight. The weights are determined by minimizing the error function involving the target log and the predicted log by a combination of local and global optimization tools. Such a procedure is known as “network training”. The training process follows the process of network validation where the problem of over-fitting of the data is addressed. The network validation is performed by sequentially hiding a well log from the training process and minimizing the error function.

An excellent treatment on PNN application in log estimation is provided in the paper Hampson et al. 2001. The workflow for the impedance estimation using the PNN scheme is given in the Figure 1.

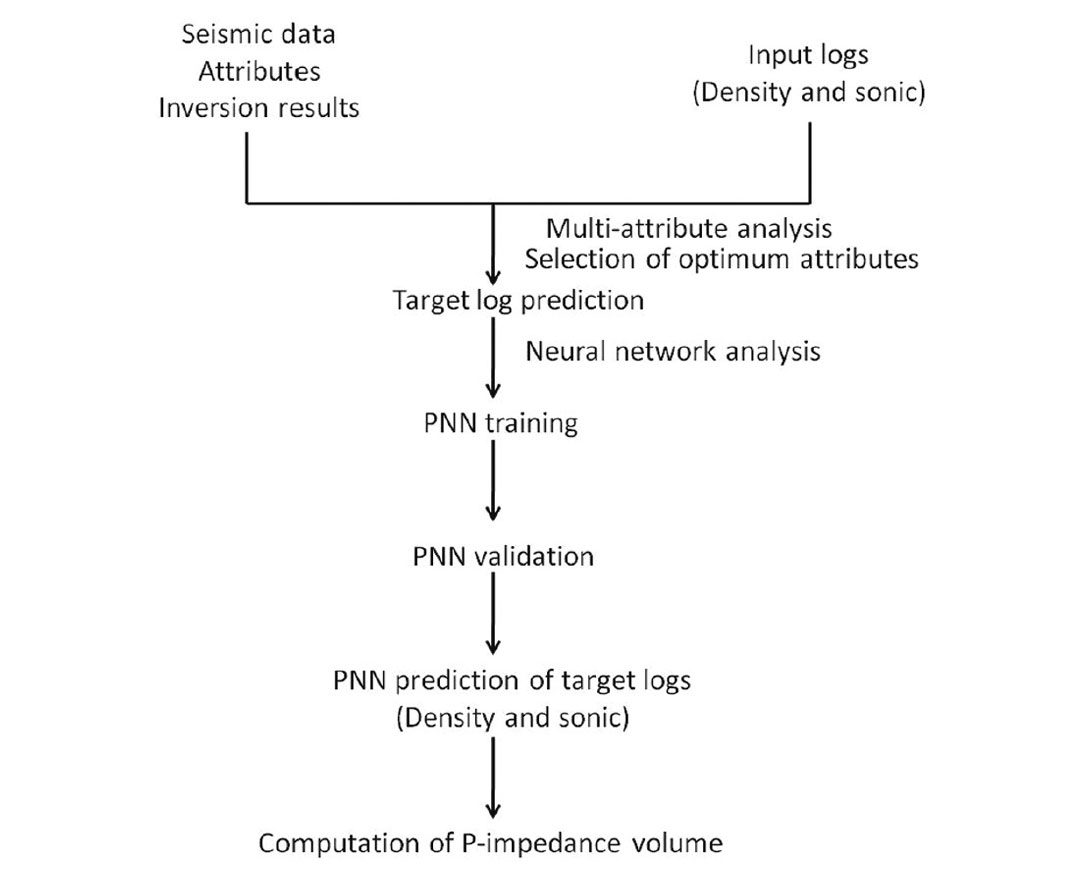
Case study

We compute the P-impedance for a 3D seismic volume from the plains of northern Alberta, Canada using the model based inversion. The area is important for the shallow gas plays and oil rich formations. We also estimate the P-impedance by individually estimating the P-wave velocity and the density using the probabilistic neural network approach. Figure 2 shows the input seismic data for the test area. A low frequency model (~10 Hz) of P-impedance is generated by using the well log followed by the estimation of a zero phase wavelet from the input seismic data. Using the wavelet and the reflectivity at a given trace location, a synthetic trace is generated from the model and compared with the seismic trace at that location, and the misfit is determined. To minimize this misfit, the initial model is updated and the process repeated. This is done iteratively till the value of the misfit drops below a desired threshold.

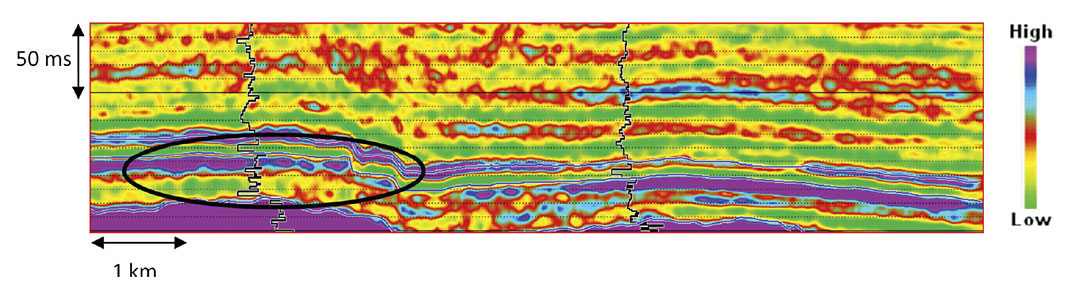
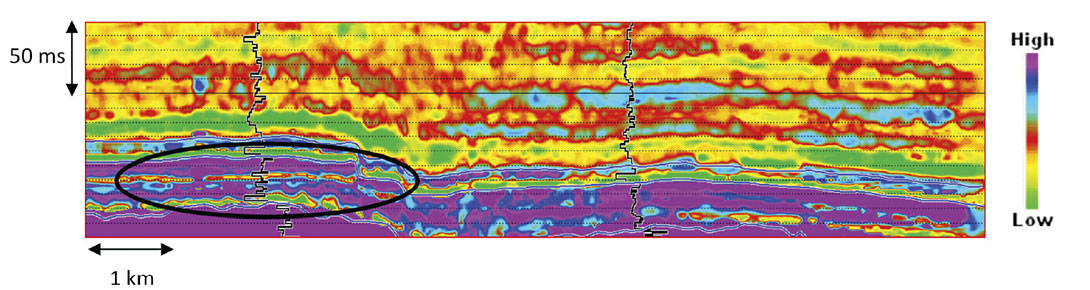
The final impedance model after such iterations is accepted as the solution of this model-based inversion procedure. Figure 3 shows the impedance section for the seismic data shown in Figure 2. We notice that the impedance shown in the highlighted zone (black ellipse) lacks detail and also the impedance does not seem to correlate so well with the overlaid impedance log.

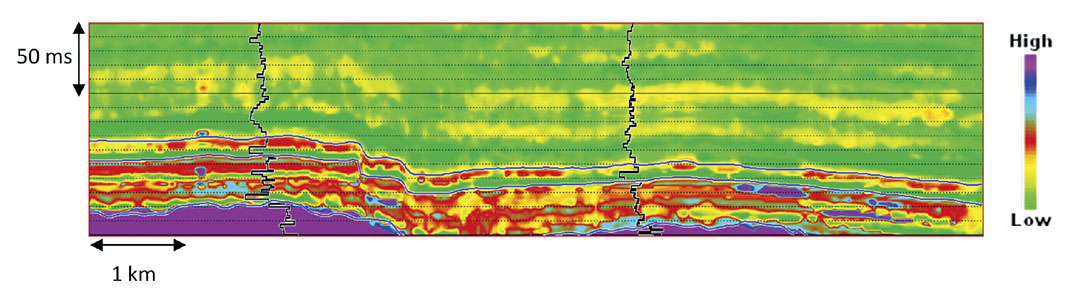
In a PNN based estimation scheme, the P-impedance is computed from the independently estimated P-wave velocity and density. A linear multi-attribute analysis was first performed to shortlist the attributes that most effectively estimated the target log. The optimized combination of different attributes was obtained by the stepwise regression analysis as described in Hampson et al. (2001). The suite of attributes thus obtained was used in the probabilistic neural network analysis for the estimation of the target logs, which in our case are the P-wave and the density logs. The estimated P-wave and the density sections corresponding to the seismic section in Figure 2, are shown in the figures 4 and 5 respectively.

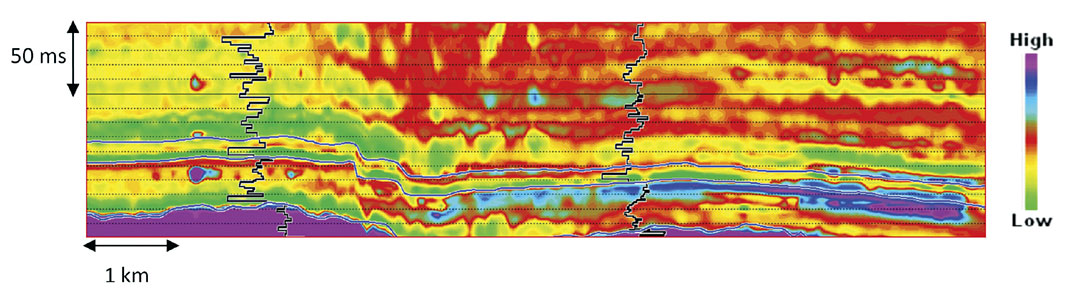
The estimated velocity and density volumes are subsequently used to compute the impedance volume. The computed impedance volume is shown in the figure 6. The zone marked within the ellipse shows that the estimated P-impedance contains information of the finer details consistent with the accompanying well log.

The inserted curves are the computed impedance logs at two different locations. The ellipse marks the zone where PNN based estimation provides more information compared to as seen in the model based inversion in the figure 3. It is also noticed that the additional information seen in the PNN estimation is consistent with the well logs.

Conclusions

Comparison of the figure 3 and figure 6 shows that the impedance obtained from the conventional model based inversion and the neural network based estimation are broadly comparable. However, the neural network based estimation provides more information compared to the model based inversion. This is clearly evident in the zone marked by an ellipse in the figure 6. A thin low impedance layer is seen sandwiched between two high impedance layers in this zone. This thin low impedance layer is consistent with the well log.

It is a common argument that the model based inversion is based on a sound mathematical platform whereas the neural network analysis operates as a kind of “black-box”. However if the inversion is highly dependent on the selected initial model because of the inherent non-uniqueness then the solution obtained is one of the many possible solutions which may be equally valid. There is no reason why a particular solution will have more preference over any other solution. For the case at hand, the neural network approach yields a solution that is geologically more meaningful, perhaps because the procedure utilizes the available well log information to estimate the target parameters. Based on our experience we conclude that for those areas where the available well-log control is uniformly distributed, the neural network approach could yield more meaningful impedance estimates that correlate well with the impedance logs. This lends confidence to the seismic interpreters to believe the impedance estimates away from the control points.

Acknowledgements

We acknowledge Arcis Corporation, Canada for the data examples included in this article as well as for the permission to publish this article.