Summary
Seismic data can be represented by a N-dimensional tensor that can be unfolded in N matrices. These N unfolded matrices (also called unfoldings) are low rank when the data are composed of a superposition of linear events. Noise and missing observations increase the rank of the unfolded matrices and, therefore, iterative rank reduction of these N unfolded matrices permits to recover missing traces and to enhance the signal-to-noise ratio of the seismic data. We propose an iterative algorithm to reconstruct multidimensional volumes.
Introduction
Reconstruction of pre-stack seismic data has received important attention in recent years because seismic data acquisition rarely leads to fully sampled wavefields. Multi-dimensional reconstruction, commonly named 5D interpolation, offers a solution to the aforementioned problem. Processes like AVO and AVAz analysis (Sacchi and Liu, 2005), multiple suppression and migration (Etgen et al., 2009) benefit from fully sampled volumes. Rank reduction methods that exploit the low dimensionality of seismic data were proposed by Freire and Ulrych (1988), Trickett (2008), Trickett et al. (2010) and Oropeza and Sacchi (2011). Methods that directly operate on the seismic data matrix, often referred as eigen-image filtering, have been proposed to denoise data in t − x (Freire and Ulrych, 1988) and f − x − y (Trickett, 2008). A new generation of methods operate on multi-level Hankel or Toeplitz matrices (Trickett et al, 2010, Gao et al., 2011). At the core of these methods is rank reduction implemented via the singular value decomposition (SVD). The basic idea is that noise-free properly sampled seismic data can be embedded into a low rank structure. Noise and unrecorded data will increase the rank of the data structure. Therefore, denoising and reconstruction can be easily implemented via iterative rank-reduction (Oropeza and Sacchi, 2010). The abovementioned methods operate on matrices or on multi-dimensional structures transformed into multi-level Hankel matrices. Recently, rank reduction methods that directly operate on tensors have been proposed to solve the multi-dimensional denoising and reconstruction problem (Kreimer and Sacchi, 2012). Tensor decompositions offer an alternative way of rank reduction. Particularly, the Higher-Order Singular Value Decomposition (HOSVD) (De Lathauwer et al., 2000) leads to a reconstruction algorithm where there is no need of embedding the multi-dimensional seismic data in multi-level Hankel matrices. In this paper, we investigate a new method that operates directly on the seismic tensor. Sequential rank reduction of unfolded matrices leads to an iterative algorithm with properties very similar to that of the HOSVD.
Theory
Consider a seismic volume with 4 spatial coordinates D(t,x1,x2,x3,x4). The DFT can be used to transform the volume to the f-x1,x2,x3,x4 domain. For each temporal frequency f, this volume can be arranged into a 4th order tensor that depends on x1, x2, x3, x4. A 4th order tensor can be unfolded in four matrices. Each unfolding is a rearrangement of the slices of the tensor in different directions (or modes) into a matrix. Figure 1 exemplifies the unfolding of a 3rd order tensor.
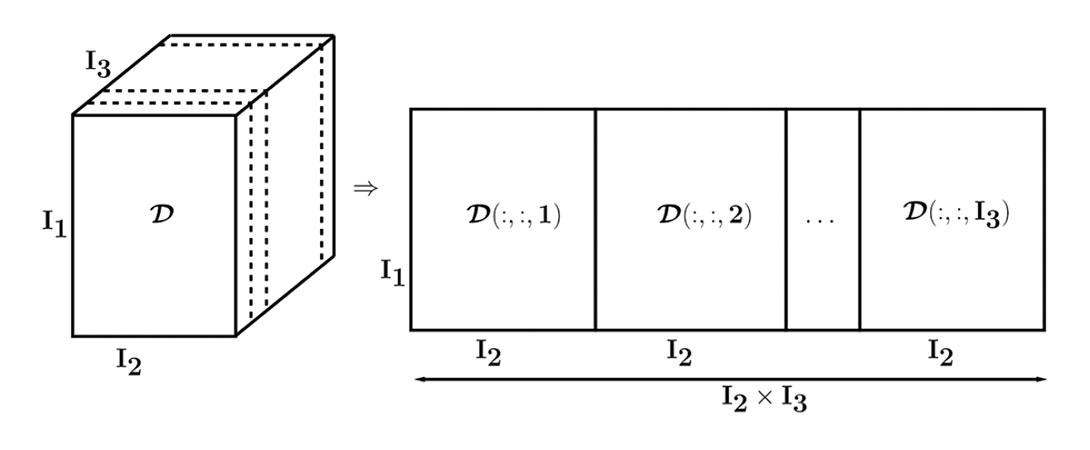
Assuming that each one of the unfolded matrices obtained from the tensor is a low-rank structure, we propose an algorithm that applies rank reduction sequentially to each unfolded tensor:

The above algorithm can be expressed in operator form via D̃ = R(D). The rank r is the desired rank and can differ for each unfolding. The procedure can be used to denoise multidimensional seismic data in a similar way f-x-y eigenimage filtering (Trickett, 2003) can be used to denoise data that depend on two spatial dimensions.
A reconstruction algorithm
The rank reduction iterative algorithm adopted by Oropeza and Sacchi (2011) and Kreimer and Sacchi (2012) for simultaneous denoising an reconstruction is given by
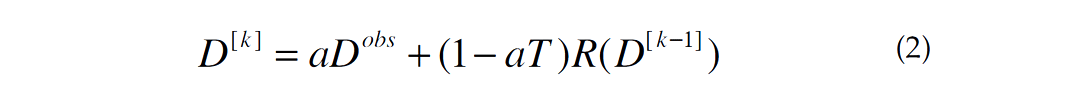
where a is a parameter between 0 and 1 that controls the level of reinsertion of noisy observations. The operator T is the sampling operator with the same dimensions of the data, filled with zeros in the bins with missing traces and ones in the bins containing samples, the index k indicated iteration number. This algorithm is similar to reconstruction via Projection onto Convex Sets (POCS). However, we notice that the POCS algorithm is implemented via an iterative amplitude thresholding process (Abma and Kabir, 2006), whereas expression (2) applies tensor rank reduction in each iteration.
Examples
To demonstrate that unfolded tensors are a low rank structure we designed a volume of size 128 x 12 x 12 x 12 x 12 that contains 3 plane waves. Figure 2a displays the distribution of singular values averaged over the 4 unfoldings. This figure corresponds to fully sampled data with SNR=100. Clearly, only a few singular are different from zero. Figure 2b corresponds to the case where the data were decimated and contaminated with noise. The spectrum of singular values shows three dominant components immerse in smaller ones that model the noise subspace.
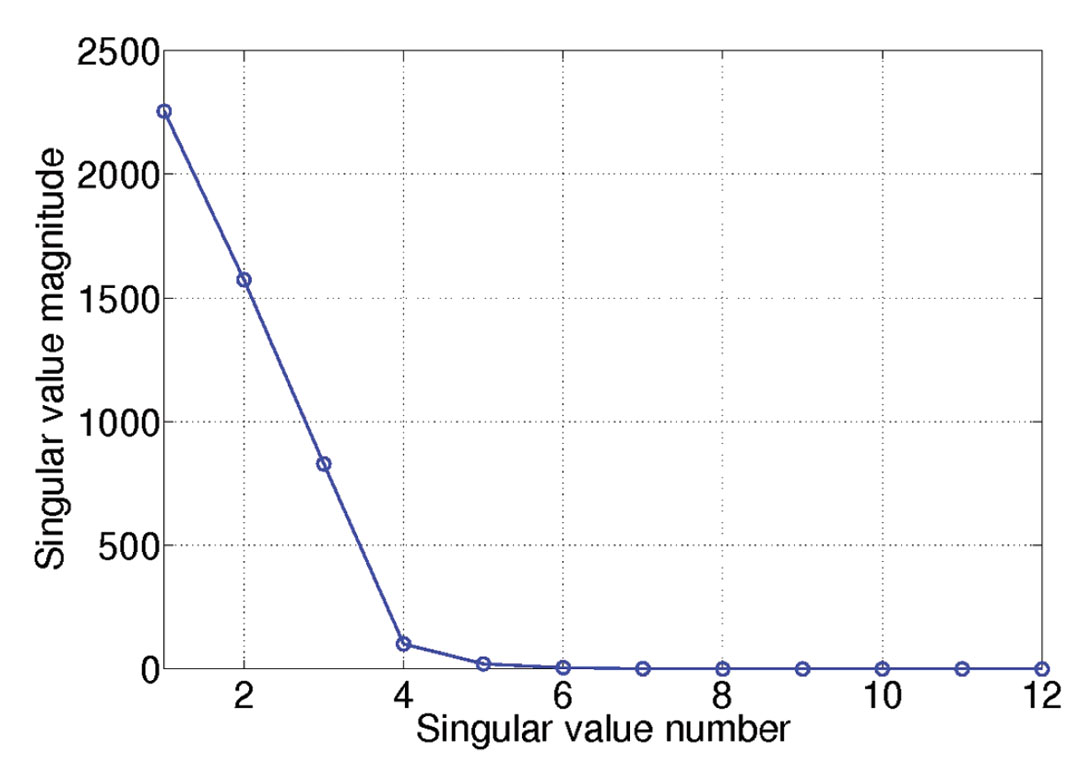
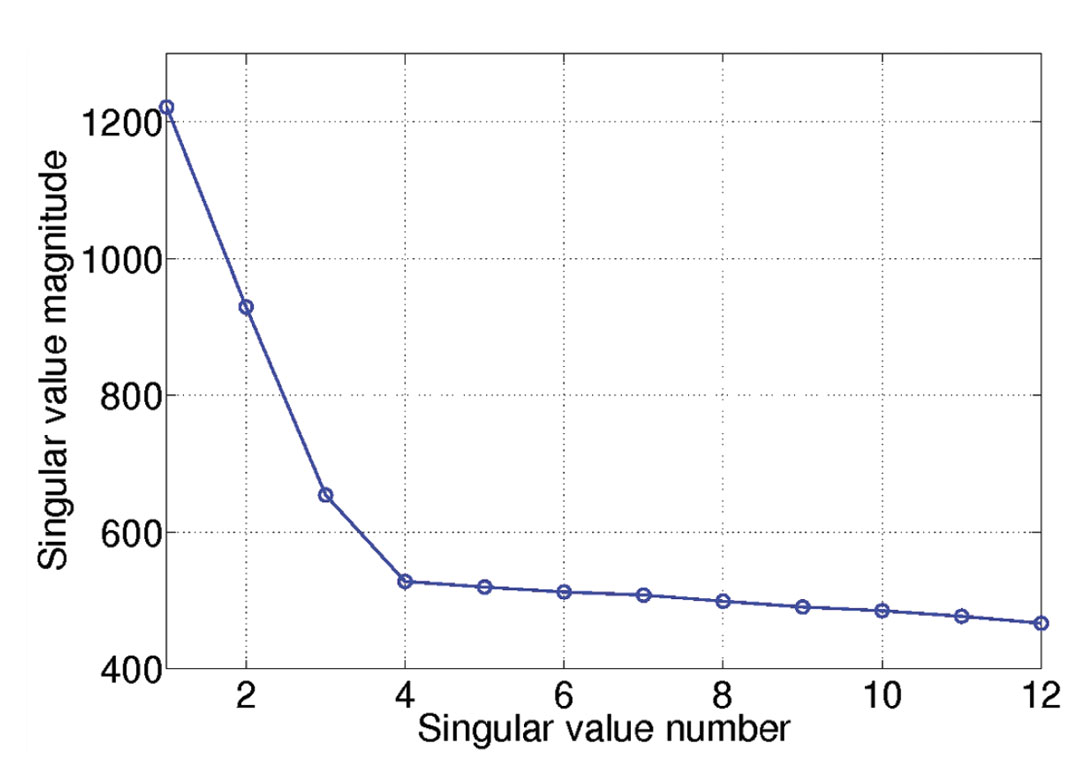
Figure 2. Distribution of singular values averaged over all 4 unfoldings, for one frequency. Case of data with linear events.
Figure 3 shows the result of applying the rank reduction procedure explained in the previous section. We have kept the first 3 singular values in each unfolding. Column (a) in the figure is the non-decimated data (prior to noise contamination), the column (b) is the decimated data after addition of noise (SNR = 1). The latter is also the input to our algorithm. Column (c) is the reconstructed and denoised data and column (d) is the difference between the first and third column (error). The reconstructed and noise attenuated volume have negligible errors. One can confirm that the algorithm is able to recover the events with a high degree of accuracy. The reconstructed volume has a Frobenius norm that is about 32 times the Frobenius norm of the reconstruction error. As a comparison, we also used the truncated HOSVD (Kreimer and Sacchi, 2012). The results were very similar to those obtained with the proposed algorithm.
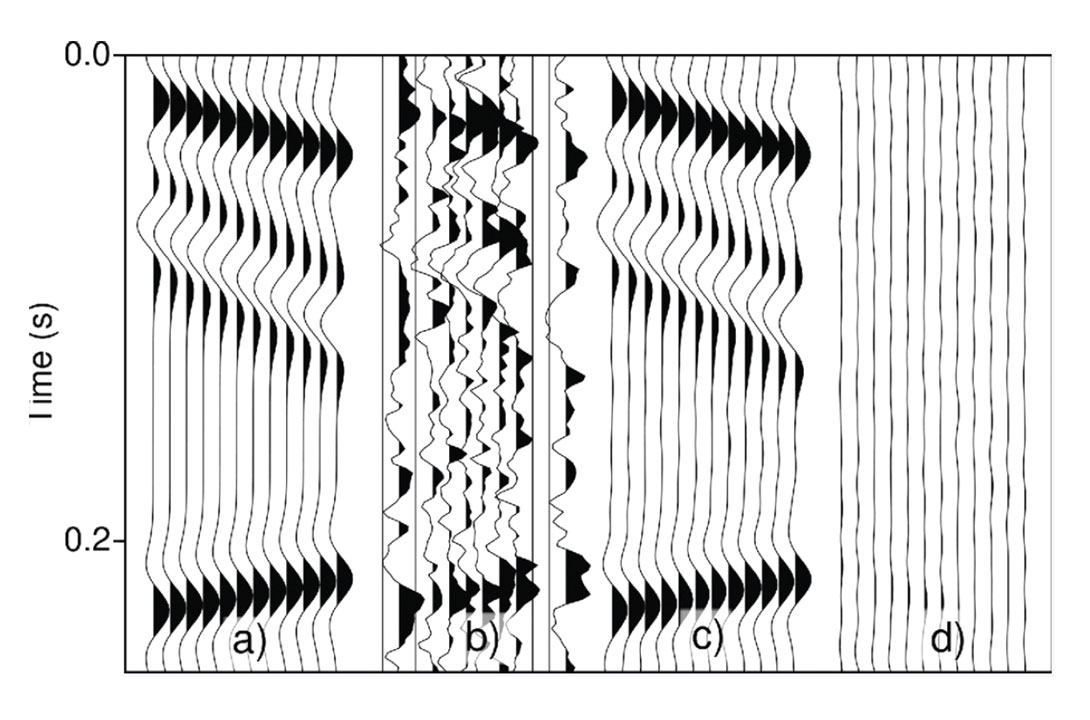
We also examine the spectrum of singular values averaged over all unfoldings for a data set composed of three curved events with 50% decimation and contaminated with noise. Figure 4 displays the distribution of singular values for this exercise. The spectra of singular values does not show an abrupt change in amplitude; a feature that can be used to reveal if the underlying data is a low rank structure. The quality of reconstruction slightly degrades with curvature. However, the reconstruction results are within an acceptable level of accuracy. The reconstructed volume has a Frobenius norm that is about 19 times the Frobenius norm of the reconstruction error. Figure 5 highlights 4 CMPs prior decimation and after reconstruction.
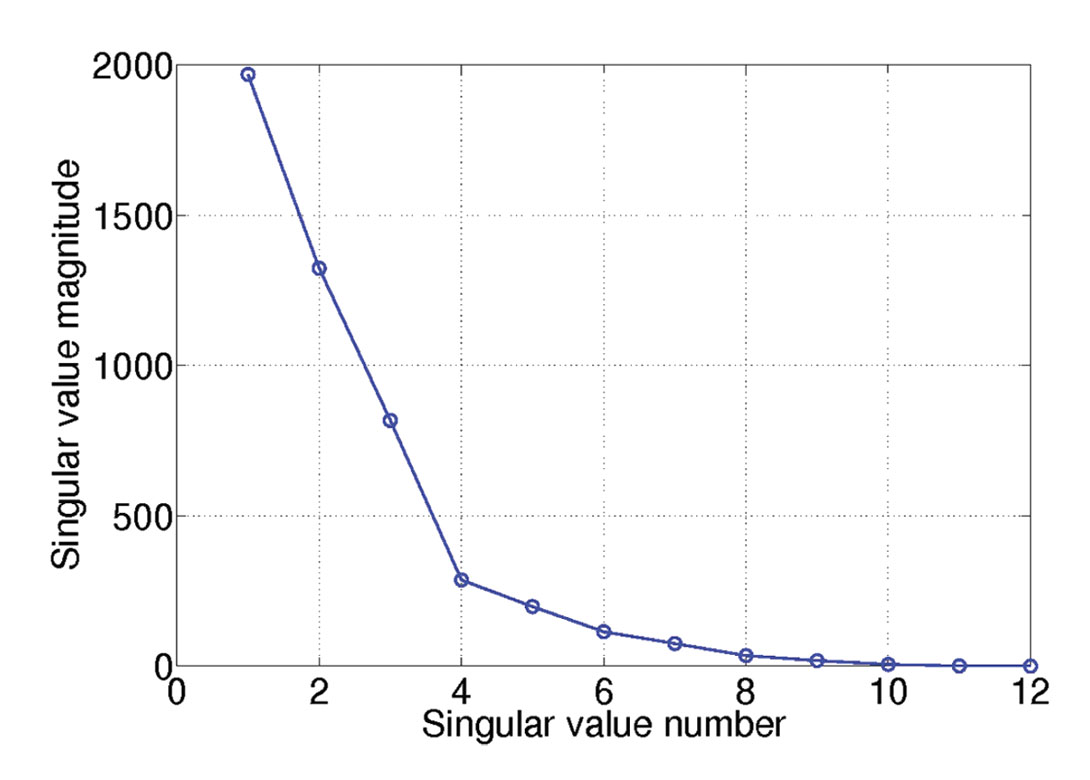
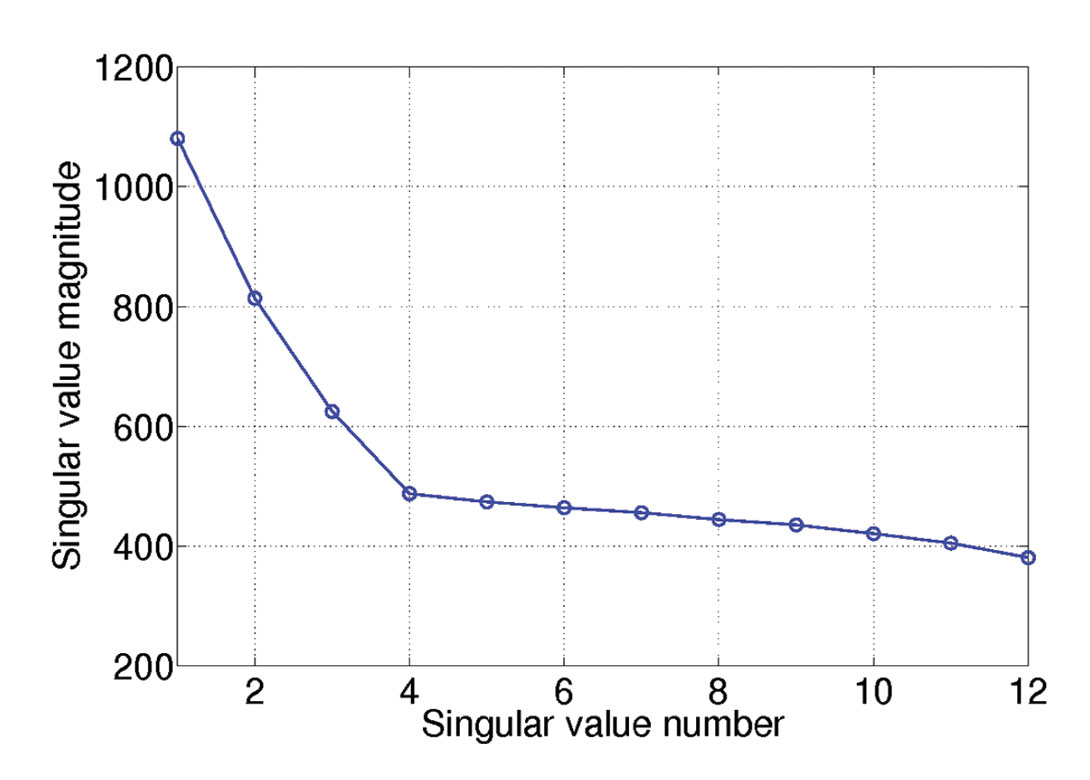
Figure 4. Distribution of singular values averaged over all 4 unfoldings for one frequency. Case of data with curved events.
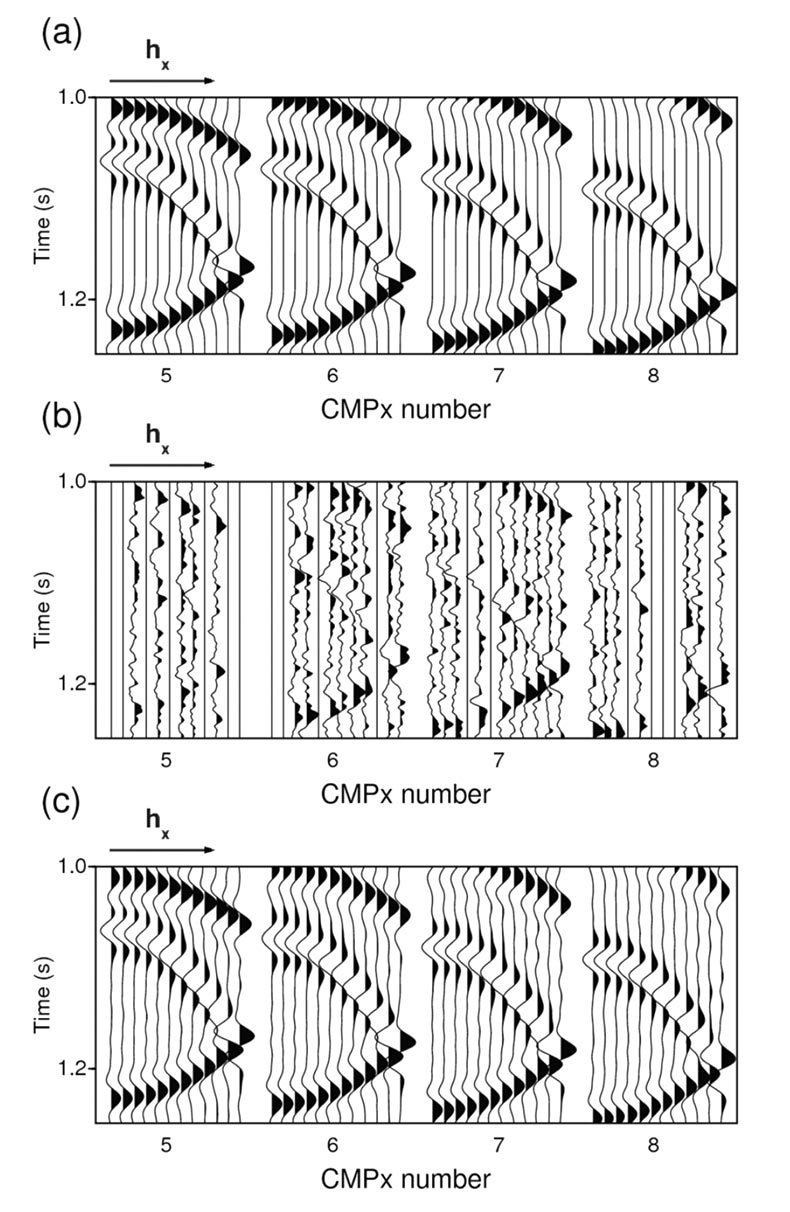
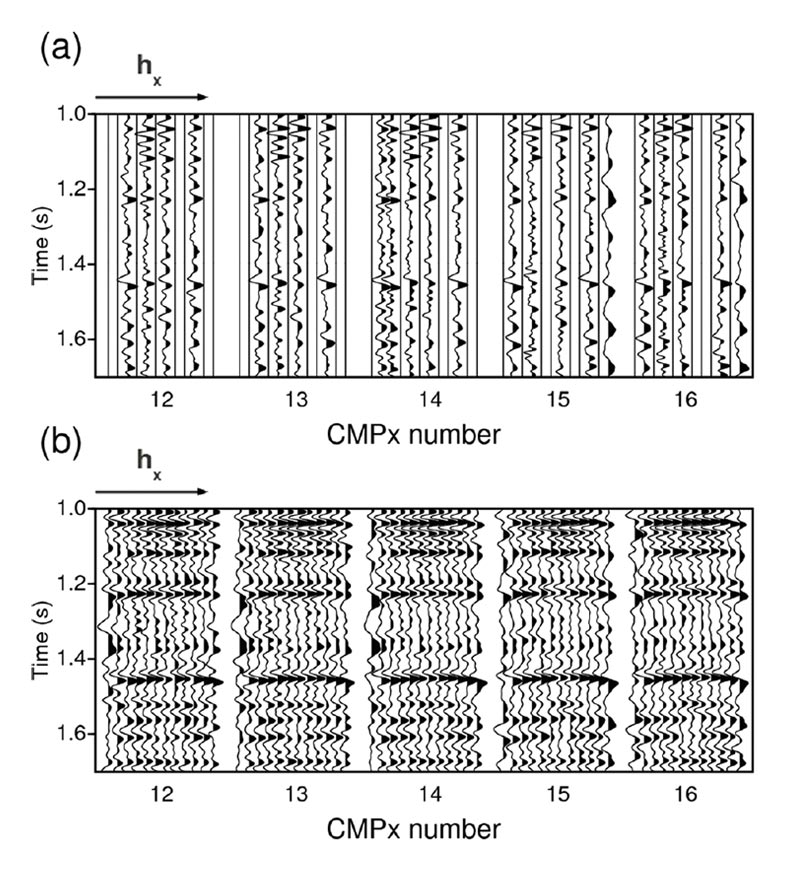
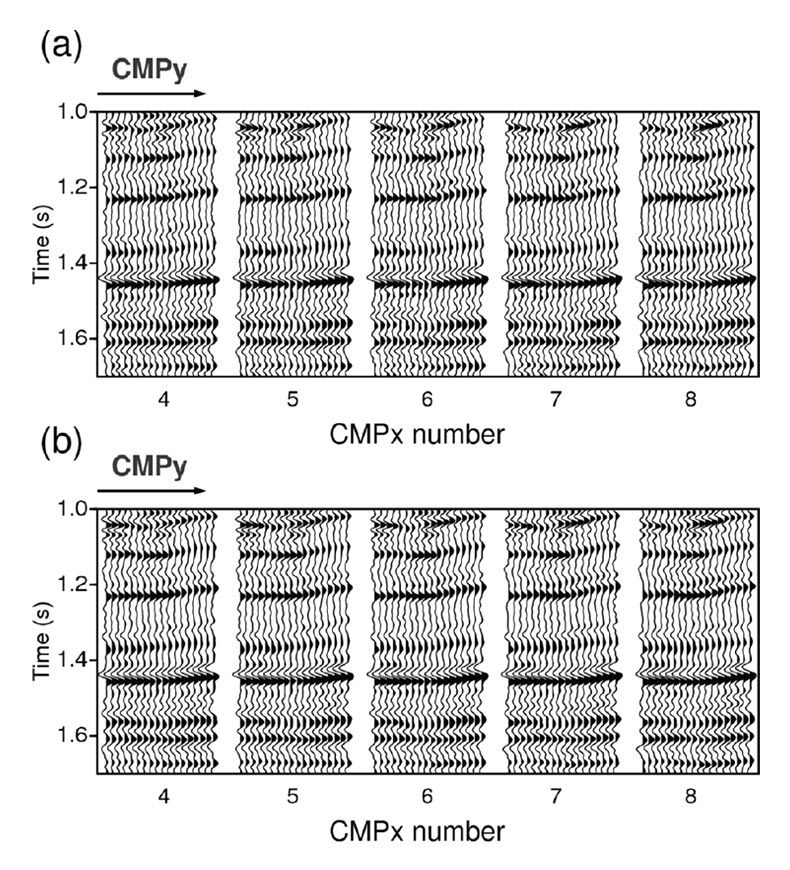
Our real data example is from the Western Canadian Basin. The reconstruction was carried out in the inline/crossline midpointoffset domain with a grid of size . The input was NMO corrected and contained 16060 traces. These traces populated 39% of the grid. Figure 6 shows 5 CMP gathers prior and after reconstruction. To assess the presence of any damage to the data during the reconstruction process, we present 5 stacked CMPs in Figure 7. We can observe some level of noise attenuation in the stacked data after the reconstruction.
a) Ideal noise free and fully sampled data, b) Decimated and noisy data, c) Reconstructed and noise attenuated data.
Conclusions
We have presented an application of the singular value decomposition for rank reduction of a tensor. The algorithm operates directly on matrices obtained by unfolding the tensor that represents the prestack seismic data in the frequency-space domain. The proposed rank reduction method applies an iterative rank reduction that permits to denoise and reconstruct seismic data. Current research directions explore the feasibility of the method to reconstruct large volumes of seismic data.














Join the Conversation
Interested in starting, or contributing to a conversation about an article or issue of the RECORDER? Join our CSEG LinkedIn Group.
Share This Article