Non-hyperbolic MultiFocusing Improves Depth Imaging

Summary

MultiFocusing technology can dramatically improve the quality of seismic imaging especially in cases of low fold data, poor signal- to- noise ratio and sparse 3D acquisition. At the same time, local parameters of the observed wavefield in prestack seismic records are of great interest for many seismic applications such as signal enhancement, velocity model building, etc. We propose to employ the MultiFocusing idea to achieve this goal. A local common offset MultiFocusing approximation for travel time stacking surface description is used. It allows an accurate approximation of travel times for reflection events in the vicinity of arbitrary location and arbitrary offset. We present the implementation of two applications: a signal enhancement scheme and velocity model construction by prestack stereotomography. We will also demonstrate efficiency of the proposed applications.

Introduction

Time imaging usually constitutes a key first step that facilitates the estimation of a velocity model for depth imaging even for complex areas that require depth migration for correct subsurface imaging. For these reasons, improving the quality of time imaging is a focus of intensive research. A recent advance is MultiFocusing (MF), a method with the potential to greatly improve the quality of time imaging.

In contrast to the procedures of CMP based methods, in the zero-offset MF approach proposed by Berkovitch et al. (1994) and described in detail in Berkovitch et al. (2008) and Landa et al. (2010), each zero-offset trace is constructed by stacking traces that need not belong to the same CMP gather but, rather, whose sources and receivers are within the limits of a certain aperture in the vicinity of the central (imaging) point. The size of such an aperture is determined by the size of the first Fresnel zone. The number of traces falling in this zone can significantly exceed the number of traces belonging to one CMP gather. This allows a considerable increase in the signal-to-noise ratio for the target reflection. Since the traces being stacked no longer belong to the same CMP gather, this procedure requires a more general moveout correction than the one used in conventional CMP stacking. For a given source-receiver pair, the MultiFocusing moveout equation is based on the spherical approximation of the reflection event’s wavefront near the observation surface. The moveout correction expressed by the zero-offset MultiFocusing (ZOMF) formula is, in the 2D case, a three-parameter surface which accurately approximates the actual travel time in the vicinity of the imaging point. The three parameters are: the emergence angle of the normal ray and the radii of curvature Rcre and Rcee of the two fundamental wavefronts, namely, normal incident point and normal waves respectively.

One of the main limitations of the zero-offset MF method is a quasi-hyperbolic approximation for actual travel-time surfaces. The MF operator in this case is constructed around a zero-offset ray and, in principle, is valid for short offsets.

In this paper, we introduce a generalization of the zero-offset MF correction for the arbitrary offset case. We refer to this new time correction as common-offset MultiFocusing (COMF). There are a number of possible applications of the COMF such as non-hyperbolic time imaging, prestack signal enhancement, AVA, stereotomography, etc. In this paper we illustrate two applications: prestack signal enhancement in case of non-hyperbolic arrival traveltimes for reflected events and velocity model building using the COMF approach.

MultiFocusing technology

MF technology, based on multi-parameter analysis of the wavefield and summation along predicted time surfaces, has been applied to enhance time imaging sections by dramatically increasing the fold of coherent summation of seismic signals. The MF correction formula is quite accurate, even for strongly curved reflectors and moderate lateral velocity variations. This can be attributed to the fact that it is not a simple hyperbolic Taylor expansion, but a double square-root equation. Implementation of the MF method is technically challenging because it requires estimation of three moveout parameters in the 2-D case and eight in the 3-D case, as opposed to a single parameter (stacking velocity) in standard normal moveout velocity analysis. It is achieved by simultaneously analyzing a super-CMP gather consisting of a number of CMPs. Although, in principle, “mixing” reflection events from a number of CMPs might compromise the spatial resolution of the resulting stacked section and make random noise appear as an interpretable signal, our implementation of a simultaneous parameter search mostly avoids this effect and minimizes artifacts.

Key potential benefits of MF stacking, as compared to the CMP stack, include:

• Stacking a large number of traces covering many CMP gathers that can increase the stacking power and signal-tonoise ratio;
• A moveout correction that is “stretch-free,” which dramatically increases vertical resolution and essentially can contribute to wide-angle amplitude versus offset analysis; and
• A moveout correction formula that accurately describes travel-time behavior for a wider class of subsurface models.

Common-offset MultiFocusing correction

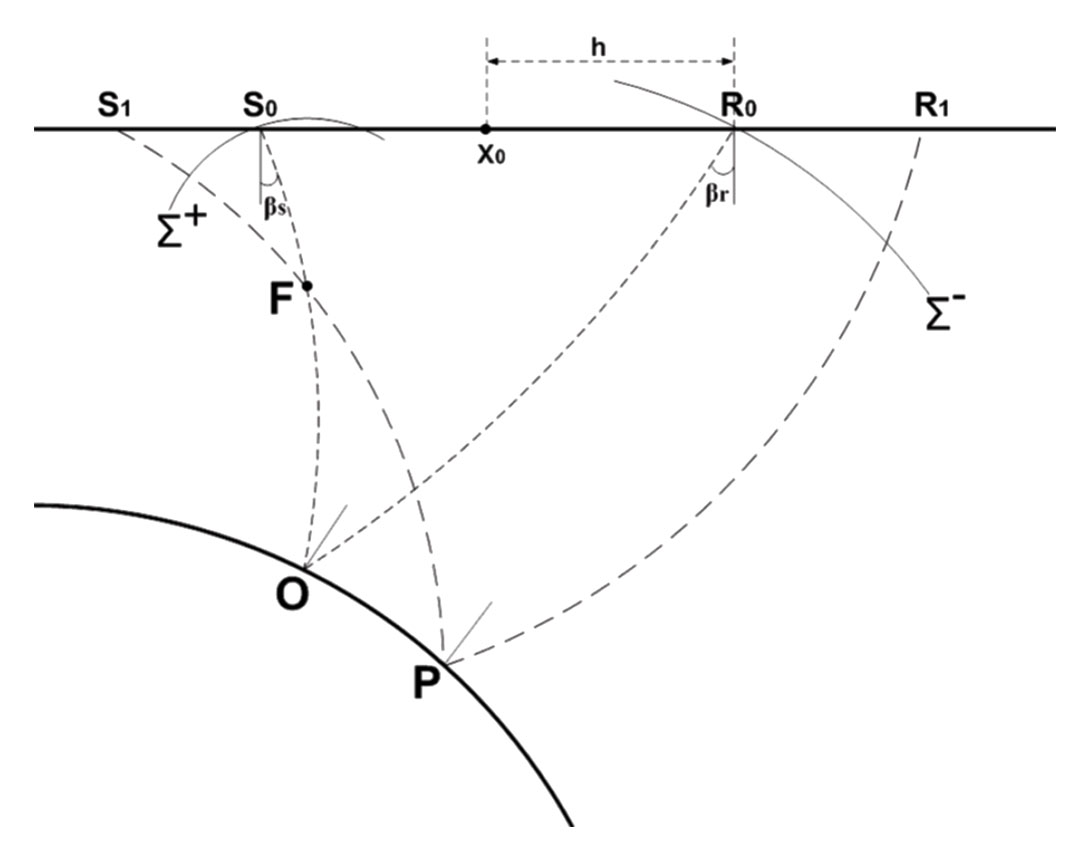
One of the main limitations of the zero-offset MF method is a quasi-hyperbolic approximation for actual travel-time surfaces. To increase the accuracy of the MF approximation and to take into account strong non-hyperbolicity of the traveltime surfaces, let us introduce a local MF time correction which will accurately approximate traveltime surface in the vicinity of an arbitrary non-zerooffset trace. Unlike zero-offset MF time approximation, it is valid for arbitrary source-receiver pairs in the vicinity of a non zerooffset trace. Figure 1 illustrates schematically the new method.

A ray starts at the surface point S₀, with the angle β_s to the vertical. This ray hits the reflector at the point, O, and returns back to the surface point R₀ with the angle β_r . A paraxial ray starts from an arbitrary source S₁ located at distance ΔX⁺, crosses the ray S₀O at point F and arrives at receiver R1 located at distance ΔX^– after reflecting at point P. Parameters, such as curvature radius and spreading function for different wavefronts propagating along the ray, can be estimated using dynamic raytheory fundamental solutions (Červený et al., 2001), allowing compact expression for the description of moveout traveltime.

Let us consider two fictitious wavefronts: Σ⁺ emitting from the point F upward to the surface, and Σ^– emitting from the point F downward, reflected at the reflector and emerging at the point R₁. These two fictitious wavefronts are characterized by two radii of curvatures R⁺ and R^-. The common-offset Multifocusing (COMF) establishes connection between two fictitious waves Σ⁺ and Σ^– and dynamic parameters of the common offset ray S₀OR₀, namely, radii of curvature of the common shot R_S, common receiver R_r and spreading function L. The travel time correction Δt in this case can be written as:

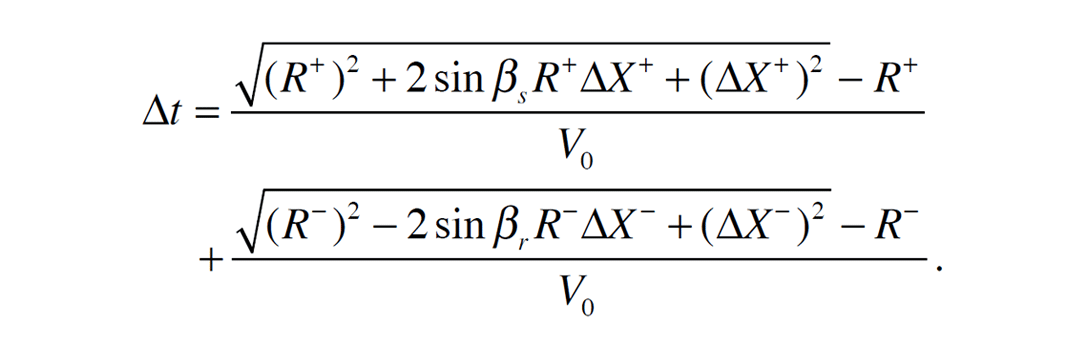
where V₀ is near surface velocity, and

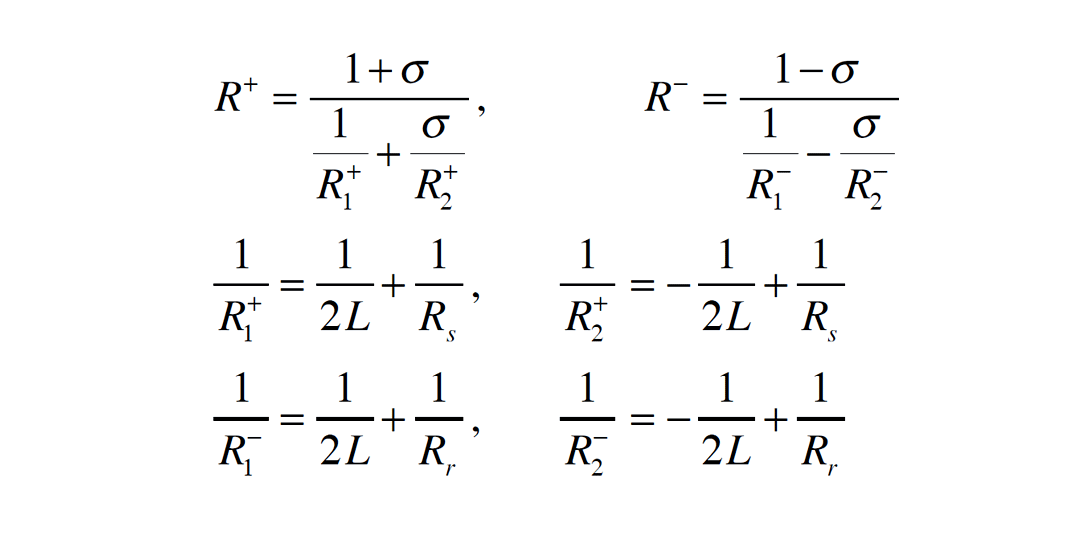
and focusing parameter σ can be derived solving the following system of equations

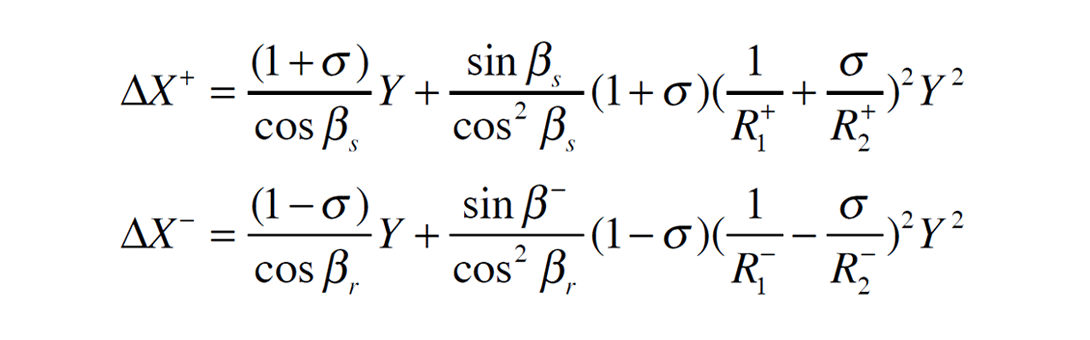
where Y is the so-called asymmetrical coefficient.

The travel time correction for arbitrary CMP position and offset h (Figure 1) is a function of observation geometry, near surface velocity and 5 unknown parameters: ΔX⁺, ΔX^-, β_s , β_r , R_S, R_r , L.

COMF traveltime formulas provide an adequate representation of arrival times for arbitrary offset and source-receiver configuration. The COMF correction formula is remarkably accurate even for strong curved reflectors. It should be emphasized that the moveout correction is an appropriate basis for the commonoffset stacking procedure, as it can align reflection events in a large gather of seismic traces (super-base) that spans many CMP gathers. Implementation of the COMF method is technically challenging because it requires defining five moveout parameters instead of three parameters in zero-offset MultiFocusing and one parameter in standard NMO velocity analysis.

Practical implementation of the COMF requires determination of five parameters for each time sample of the common-offset image. Analysis consists of calculating a panel of correlation measure (e.g., semblance) as a function of unknown parameters, and choosing an appropriate correlation maximum. A manual procedure for MultiFocusing is impractical and an automatic mode is necessary. The developed procedure is based on coherency measure calculation and analysis of the MultiFocusing super-gather. The procedure consists of data correction according to different traveltime curves using the time correction equation and finding parameters, which correspond to the coherency measure maximum. The correlation procedure is repeated for each imaging point, for each offset and for each time sample. It is important to note that the described procedure can be applied locally within a small vicinity of each seismic trace and does not require global full offset approximation. In this way, we avoid hyperbolic or quasi-hyperbolic approximation for traveltime curves/surfaces as it is usually required in most time imaging procedures such as CMP, PSTM, ZOMF, etc. Outputs of the COMF are partially stacked common-offset sections and optimal wavefront parameters of the total wavefield. The results can provide enhanced prestack seismic records and the results can be used as accurate and reliable information for velocity model construction and subsequent depth imaging.

Enhanced seismic gathers

In many situations, the un-migrated time image itself can be regarded as a by-product, and the improved prestack seismic traces with increased signal-to noise-ratio are requested. Typical examples of such situations are velocity model-building or prestack time or depth migrations. The idea of using accurate traveltime approximation for prestack signal enhancement is not new. Both MultiFocusing and common reflection surface stack (CRS) can be used for this purpose (Baykulov and Gajewski, 2009, Buzlukov et al., 2010). But the global, quasi-hyperbolic zero-offset operator used in these methods limits the efficiency of this application for cases of complex geology and/or strong lateral velocity variations. In these cases, the traveltimes of seismic events become non-hyperbolic and MF/CRS zero-offset operator approximation starts to be inaccurate. Similar effects can be caused by anisotropy or large offsets.

Wavefield parameters estimated by the COMF method can be used for prestack data regularization and enhancement. The idea is to apply the COMF traveltime formula to compute partially stacked gathers, in which each trace is a result of summation of data along the local COMF stacking surface.

The number and location of traces in the produced gathers can be different from the input locations, and the resulting traces can be regular with increased signal- to-noise ratio due to partial coherent summation. The signal enhancement procedure consists of two steps: parameter estimation for each defined trace on each common offset section, and then, according to the estimated COMF parameters, the partial stack calculates a stacking time surface around a specified CMP-offset location and performs the summation of data along that surface. The result of the summation is assigned to the same CMP, offset, and time coordinates. Repeating this procedure for all desired points generates a new gather that is called the COMF enhanced gather.

Seismic events at about 2.5-3.5 sec are characterized by strong non-hyperbolic arrivals due to a strong velocity anomaly in the model. Figure 3a shows the same CMP gather after applying zero-offset MF signal enhancement when the enhancing operator was estimated using zero-offset MF approach. As expected, a non-hyperbolic part of the events was deteriorated by noncoherent summation along a hyperbolic operator defined by ZOMF. Figure 3b shows the gather after applying COMF signal enhancement. A partial stacking operator was developed through estimation of five parameters for each CMP position, each offset value and each time sample. Aperture for estimation was 125m in CMP direction and 250m in offset direction. The resulting gather shows perfect reconstruction of the non-hyperbolic part of the gather.

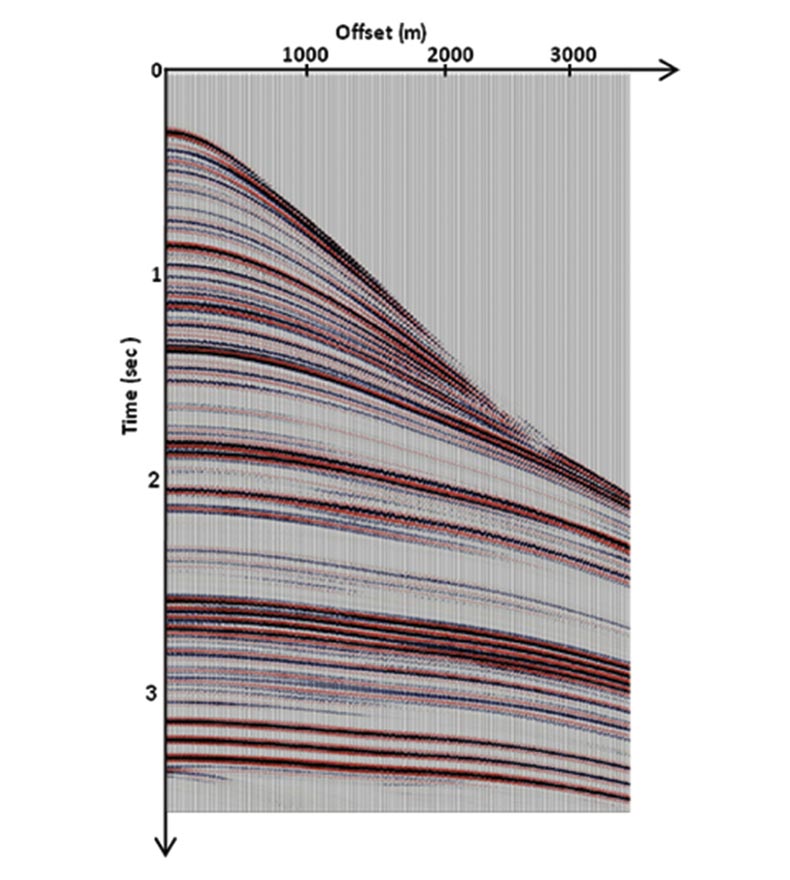
To illustrate correctness and efficiency of our procedure we performed prestack depth migration using original data with random noise added and both sets of the enhanced gathers for the true velocity model shown in Figure 5a.

Figure 4a shows the PSDM result using the original gathers. Figure 4b is a depth section obtained from gathers enhanced by the zero-offset MF operator and Figure 4c illustrates the PSDM section using the COMF operator. As it was expected, differences between the two images appear at places where the arrival traveltimes on the original gathers are strongly non-hyperbolic. Of course, data computed using the COMF operator produces a depth section closer to the original one while gathers obtained by the ZOMF operator produce a depth section which is deteriorated at places where non-hyperbolicity on the original gathers appears (marked by circles).

Velocity model by stereo-tomography

Most of the advanced velocity model estimation methods use traveltime information. It is proposed that stereotomography opens a way for velocity model building without requiring interpretation of continuous reflection events. It is based on the principle of the Controlled Directional Reception method and it uses the idea of locally coherent events. These events are described by shot- receiver positions, two-way traveltime, and slopes at the shot and the receiver. These five parameters provide all the necessary information for velocity macro-model calculation.

Let us briefly recall stereotomographic principles. A stereotomographic data set consists of N picked locally coherent events

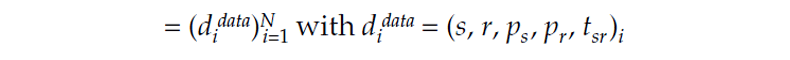
where s and r are the source and receiver locations, t_sr is the two-way traveltime, and p_s and p_r are the horizontal components of the local slopes at source and receiver, respectively, estimated on common shot and common receiver gathers. These slopes correspond to the horizontal components of the slowness vectors emerging at the source and receiver. The model m is described as N-pairs of ray segments and a smooth velocity field C. In this approach, the cost function is defined as a misfit for all components of input data d_i^data; the pairs of ray segments and the velocity model are estimated jointly by a local optimization technique based on a conjugate gradient-type algorithm.

Lavaud et al. (2004) proposed picking locally coherent events in poststack rather than in the prestack domain. Poststack picking is a reliable procedure and widely used in seismic interpretation. The picked zero-offset traveltimes, together with associated kinematic parameters, namely, radii of wavefront curvatures and emergence angles for the normal ray estimated by the ZOMF from the prestack can then be recalculated into the information necessary to perform stereotomography. Poststack stereotomography is a robust way for reliable macro-model estimation without using prestack traveltime picking or PSDM. But one principal limitation was not resolved: the hyperbolic assumption for CMP reflection traveltimes.

To overcome this hyperbolic assumption, residual poststack stereotomography was proposed which requests analysis of the residual movout correction (Neckludov et al., 2006). Alternatively, knowledge of local wavefront curvatures and emergence angles for non-zero-offset traces is required. This is exactly the information provided by the COMF method. The main advantage of this approach is the fact that picked events do not need to be interpreted in terms of reflection on any particular interface. We pick locally coherent events in the MF partial stacked (enhanced) common-offset time domain. Picking performed on a partial stacked section provides reliable information on non-zero-offset reflection or diffraction arrival times. COMF stack is also used to extract kinematic reflection wavefront parameters such as angle of emergence of the non zero-offset ray. We use the picked times and the corresponding slope information in stereotomography to estimate the velocity model of the subsurface.

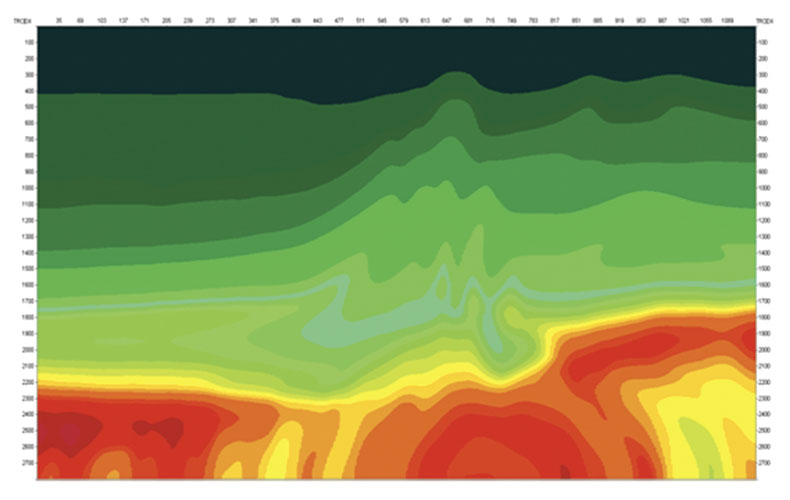
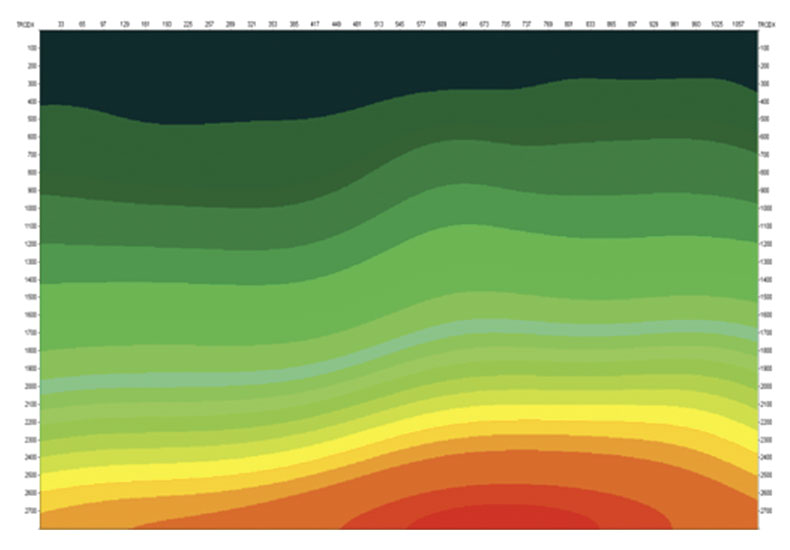
To illustrate the use of COMF for velocity model construction, we computed a synthetic seismic line for the complex velocity model shown in Figure 2. One hundred and fifty shot gathers were computed using Born modeling. Each shot gather consists of 48 traces with minimum offset of 50 meters and 50 meters intertrace distance. First, we estimated the radii of the wavefront curvatures and emergence angles for the normal rays and computed the zerooffset MF stacked section. Picking locally coherent events on the MF section and using the estimated MF parameters, we computed non-zero-offset arrival traveltimes and angles. Inverting this information by poststack stereo-tomography velocity model shown in Figure 5b was obtained.

It strongly resembles the true model (Figure 5a), but has several important differences due to low frequency spline parameterization and traveltime quasi-hyperbolic approximation in ZOMF.

Next, we estimated wavefront parameters using COMF and used this information as input to stereotomography with the same scale of the velocity grid. The resulting velocity model is shown in Figure 5c.

Now the estimated velocity is closer to the true one. This is confirmed by PSDM images (Figures 6). The depth section obtained using the velocity estimated from the COMF (Figure 6b) is closer to the true one (Figure 4d) than the depth section obtained using velocity estimated from ZOMF (Figure 6a).

Conclusions

Common-offset MultiFocusing can be considered as a method for full prestack wavefield analysis and imaging. The method is based on a local MultiFocusing approximation for locally coherentseismic events and allows, for each trace and each time sample, an accurate estimation of the wavefield parameters (such as local wavefront curvatures, geometrical spreading and emergence angles in shot and receiver domains). This information has a wide range of important seismic applications. We have presented and illustrated two of them: prestack signal enhancement and velocity model building. The first produces partially stacked common offset sections and/or prestack gathers with enhanced signal-to-noise ratio. The resulting gathers can be used for velocity model building and depth imaging using conventional methods. The second application is velocity model building using a stereotomographic approach when input information for velocity inversion is taken from the COMF analysis. Examples presented illustrate efficiency and reliability of both applications.