Improvements in microseismic data processing using sparsity and non-linear inversion constraints

Abstract

This study explores improvements obtained in microseismic data processing through the application of inversion techniques that utilize sparse and non-linear constraints. Specifically, we present a method for de-noising microseismic traces and a method for the automatic time picking of microseismic events. The de-noising method is based on a sparsity constrained time-frequency transform which is obtained by finding a sparse representation of the input data in terms of a dictionary of complex Ricker wavelets. The utilization of a complex wavelet dictionary possesses the advantage that signals with arbitrary phase can be represented with enhanced sparsity. The automatic time picking method consists in the recovery of a blocky version of the short-termaveraging/ long-term-averaging (STA/LTA) curve through inversion using a non-linear constraint. Examples of the implementation of both methods are presented using synthetic and real microseismic data.

Introduction

In oil and gas wells, microseismicity induced during hydraulic injections is characterized for its small magnitude (Maxwell, 2005; Shemeta and Anderson, 2010). This important reason is why microseismic records often display a low signal-to-noise ratio (SNR). Accuracy and reliability of the location and other event attributes derived from microseismic traces are influenced by this strong noise content (Maxwell, 2009). The relatively recent growth of interest in microseismicity analysis in the petroleum industry opens an area of opportunity to apply the vast amount of signal processing knowledge previously developed in signal analysis and imaging processing. In this study, we give a step into this area of opportunity by implementing methods for de-noising and automatic time picking using inverse regularization approaches taken from other areas of geophysics and engineering. The de-noising method is based on a spectral decomposition technique originally developed for seismic data interpretation. Following the exposition by Bonar and Sacchi (2010), we seek a sparse representation of the microseismic signal in terms of a dictionary of complex Ricker wavelets. By imposing sparsity and misfit constraints to the decomposition process, we find a de-noised version of the original signal (Chen et al., 1998, Vera Rodriguez et al., 2011). The automatic time picking algorithm is based upon the recovery of the standard short-term-averaging/long-termaveraging (STA/LTA) (Allen, 1978) curve using an inversion with a constraint that results in a non-linear system of equations. In this case, the selection of the constraint is directed towards the recovery of blocky versions of the STA/LTA curve (Sabbione and Velis, 2010). Such a constraint has also been used to invert for the earth’s relative impedance profile (Walker and Ulrych, 1983) and medical imaging applications (Charbonnier et al., 1997).

De-noising method

The decomposition of a discrete seismic trace s[n] in terms of dilations and translations of a reference complex wavelet w[n] is given by (Bonar and Sacchi, 2010)

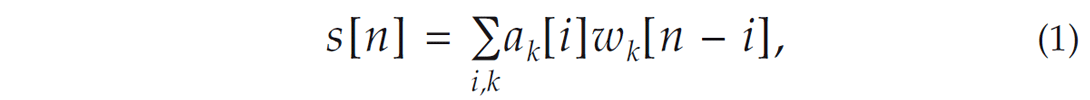
where the indexes i and k are related, respectively, to the translations and dilations of w[n], and the complex coefficients a_k[i] control the amplitude and phase of the wavelets. In matrix-vector notation, equation (1) is written as the convolution of a set of complex coefficient vectors {a_k} with a set of dilated versions of the reference wavelet {w_k}, this is

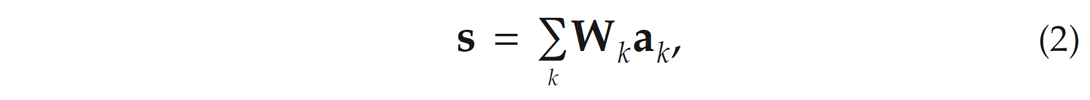
where W_k is the convolution matrix of the wavelet with dilation index k. In order to generalize this model, the convolution matrices of a set of N dilated versions of the reference wavelet can be incorporated to create a redundant dictionary R (Mallat, 2008),

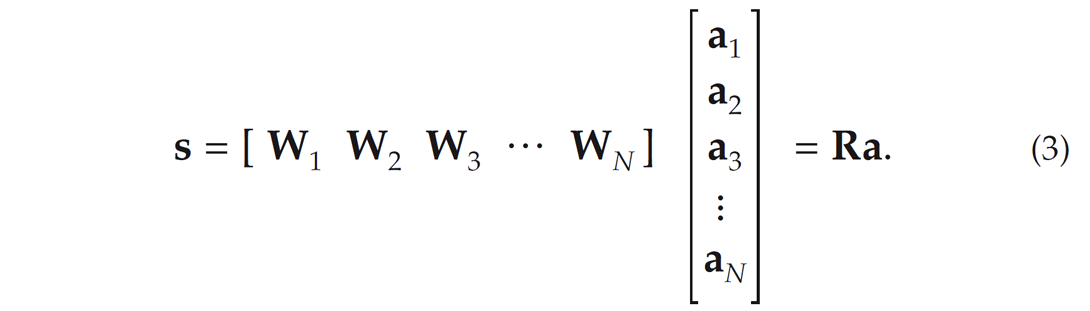
Equation (3) is an under-determined system that accepts an infinite number of solutions. In other words, there are multiple possible representations of s in terms of linear combinations of the columns of R. One alternative solution that presents advantages for de-noising purposes entails using an ℓ₁ regularization term. In other words, we will impose sparsity on the coefficients needed to represent the seismogram. This is accomplished by solving

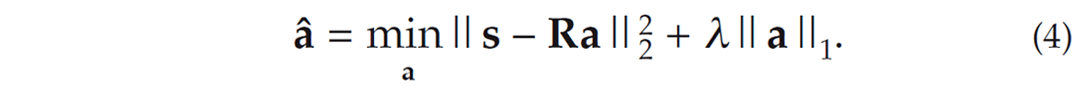
The trade-off parameter λ balances the fidelity of fit versus the amount of sparsity in the solution vector. Sparse solutions in this study are estimated using the Fast Iterative Soft Thresholding Algorithm (FISTA) (Beck and Teboulle, 2009). Other methods that could also be used to solve (4) are Basis Pursuit (BP) (Chen et al., 1998) and Orthogonal Matching Pursuit (OMP) (Pati et al., 1993). The de-noised seismic trace can then be obtained from the sparse solution â via

Automatic time picking

An efficient algorithm for automatic time picking is the shortterm- averaging/long-term-averaging (STA/LTA) filter. Changing the previous notation such that s[n] = s_n, the STA/LTA curve is defined by

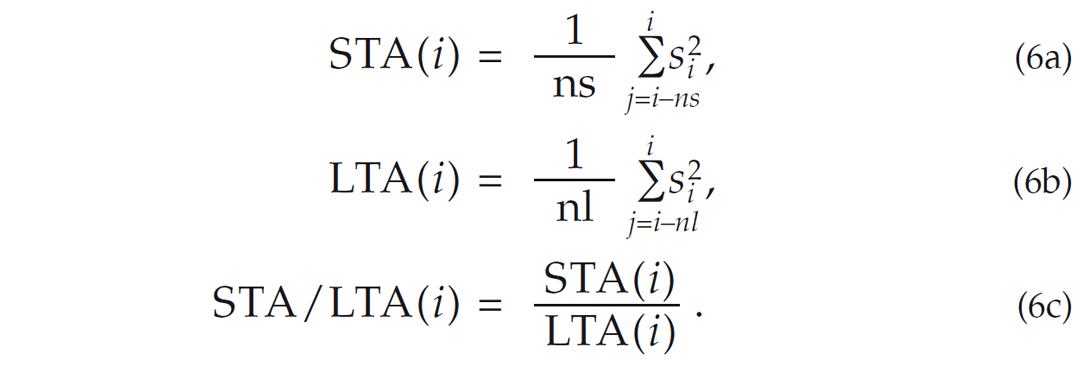
Time picks are often determined through amplitude thresholding of the STA/LTA curve. Inaccurate time picks are commonly the result of the slow build up of the STA/LTA curve from the time of the wave arrival until the time where the curve surpasses the user defined threshold. An alternative method to reduce the inaccuracy of the time picks is through the recovery of blocky STA/LTA curves from inversion. This is obtained by the minimization of the cost function

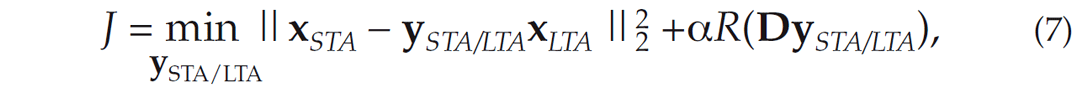
where the vectors x_STA, x_LTA and y_STA/LTA are the time series given by equations (6a), (6b) and (6c), respectively. The scalar α is a trade-off parameter, D is the first derivative matrix, and R(x) is a non-linear norm. One possibility for R(x) is

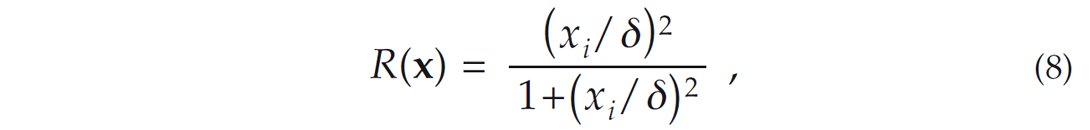
where δ is a stabilization factor. The solution to the minimization of (7) is obtained through iterative schemes such as Iterative Reweighted Least Squares (IRLS).

Examples

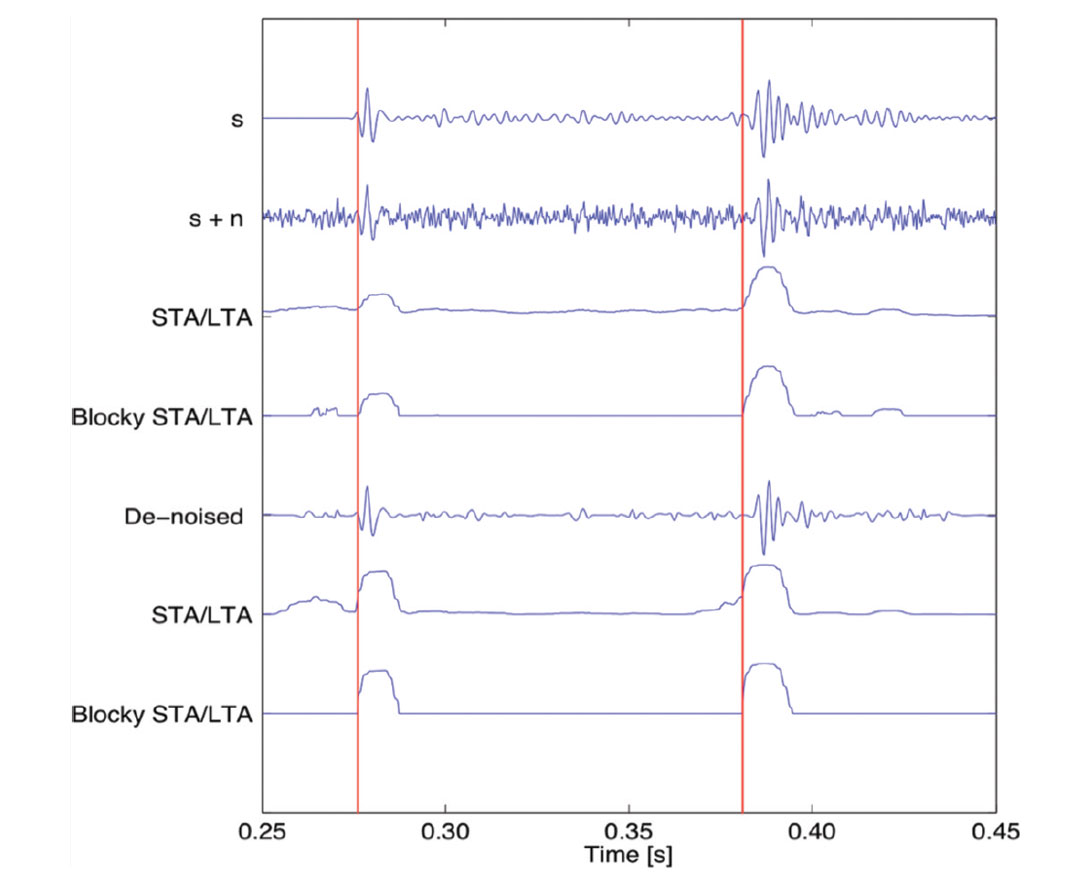
The application of the previously described methods is first demonstrated on a synthetic microseismic trace computed in a horizontally layered medium. Random noise is added to the synthetic trace using the relationship SNR = μ_s/σ_n, where μ_s is the expected signal value and σn the standard deviation of the noise. The SNR is set to a value of SNR = 3, and the resulting noisy data is de-noised using the sparse time-frequency transform (Figure 1). When compared against a low-pass filtered version of the noisy synthetic trace, the improvement of the sparse de-noising result is clear. Not only was more random noise eliminated, but also the frequency content of the arrivals of interest was preserved. Figure 2 presents the results of applying the standard and blocky STA/LTA filters to the previously described synthetic trace. The most straightforward method to set time picks in the STA/LTA curve is through amplitude thresholding. A visible difference in the maximum amplitude of the “boxes” that denote the arrivals of P and S waves in the STA/LTA curves is observed when the filters are applied over the noisy data. This means that if the thresholding level is set too high, the P arrivals could be missed. On the other hand, a thresholding level that is too low would produce multiple time picks that do not correspond to actual wave arrivals. Although the problem of false picks is partially alleviated using the blocky STA/LTA curve, improved results are obtained after de-noising the data. In the de-noised version of the data, the difference in the maximum amplitude between the P and S “boxes” is reduced. Furthermore, the blocky STA/LTA curve is cleaner than the standard STA/LTA curve before the first arrival.

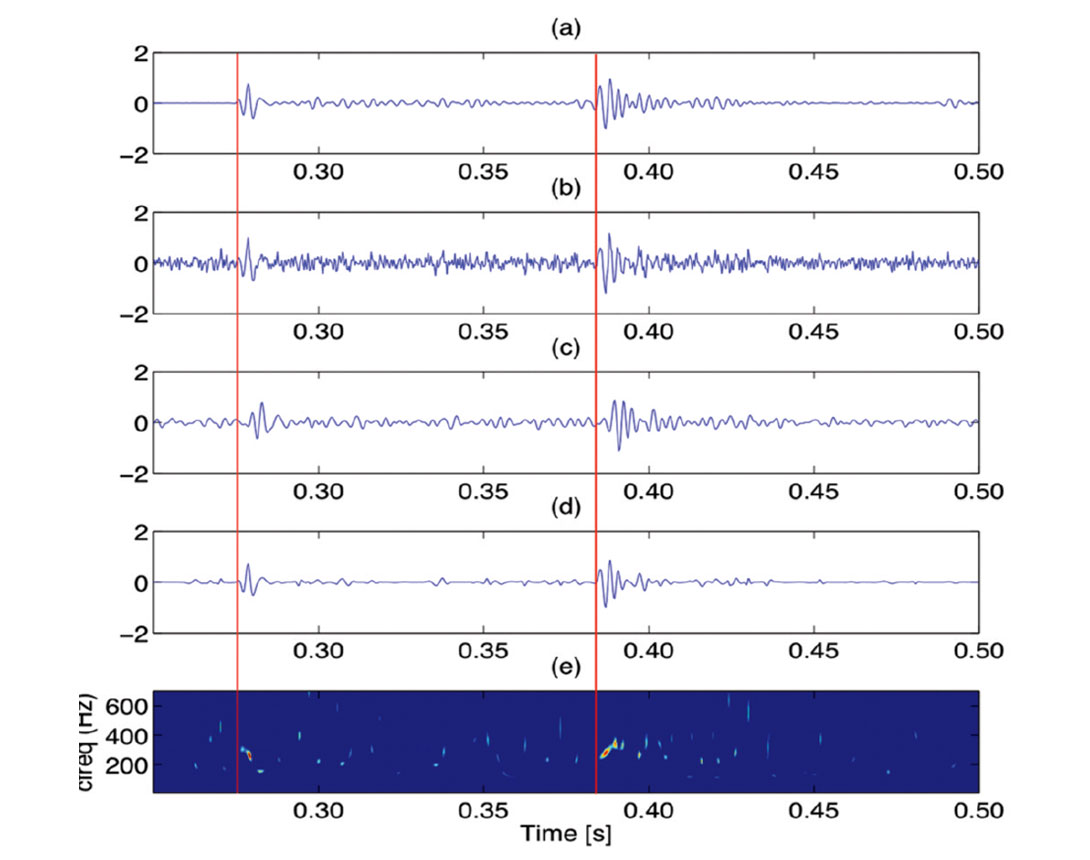
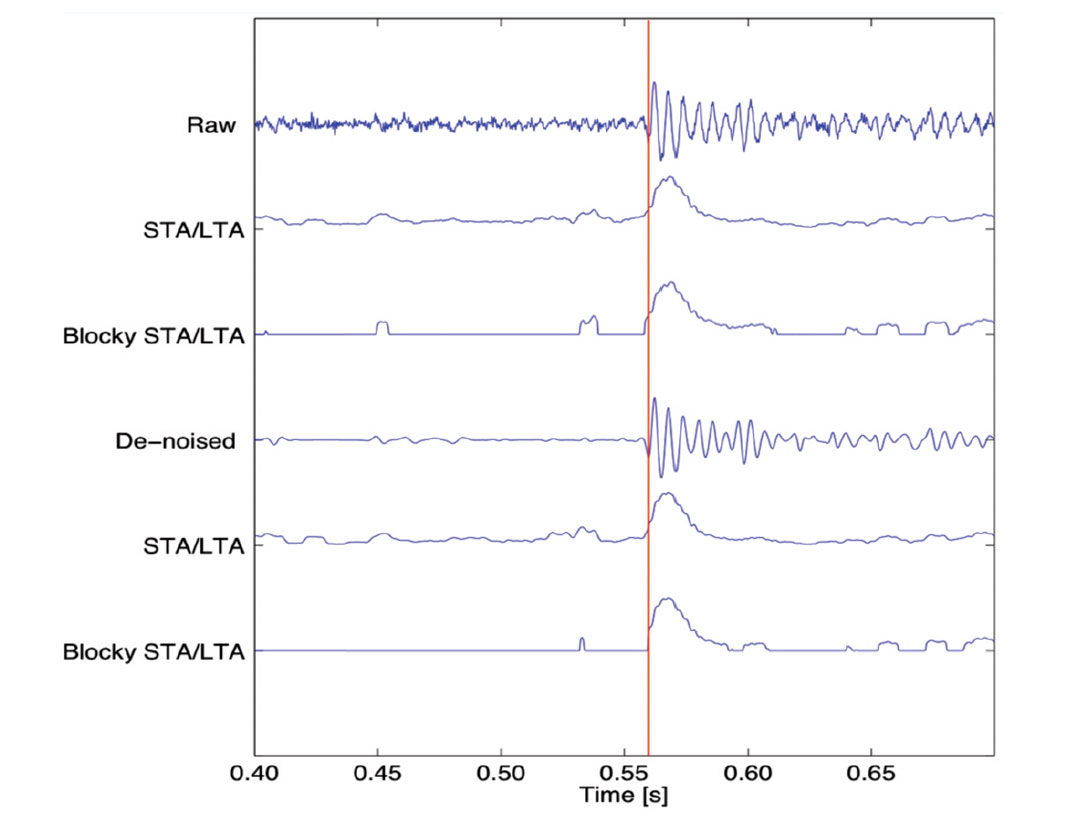
The second data example corresponds to an actual microseismic record (Figure 3). In this trace a wave arrival is visible around 0.56 s with ambient noise affecting the entire record. The denoised result displays a visible improvement in SNR, while the pulse shape and time location of the arrival of interest is preserved. This suggests that the sparse transform has not substantially affected either the phase or frequency content of the arrival. The standard STA/LTA curves in both the raw and denoised traces display a slow build up at the position of the arrival which, as stated before, introduces error in the automatic time picking process whose amount depends on the threshold value selected by the user. The blocky behavior of the inverted STA/LTA curves helps to reduce this error.

Conclusions

Processing of microseismicity records is a challenge due to, among other problems, the low signal-to-noise ratio displayed by the signals of interest. Application of techniques and processing tools developed in other knowledge areas can be of great advantage to deal with microseismicity records. For instance, in this work we applied inverse regularization techniques previously used for reflection seismology data processing and image processing. The results observed in synthetic and real data show the efficacy of the methods described to remove ambient noise without affecting the phase or frequency content of the signal of interest, and to improve the accuracy of automatic time picks.

Acknowledgements

This work was partially supported by the Signal Analysis and Imaging Group (SAIG) and Pinnacle/Halliburton. We also acknowledge Fairborne Energy Ltd. for providing the real data example.