Summary
Although microseismic monitoring of hydraulic fractures has primarily been concerned with the dimensions, complexity, and growth of the fractures or fracture systems, there is an ever-increasing desire to extract more information about hydraulic fracturing and/or natural fractures from microseismic data. Source-mechanism analysis, which is concerned with deducing details of the failure process from the microseismic waveform data, is therefore attracting more attention. However, most of the studies focus on the moment tensor inversion and much less on extracting fault-plane solutions (FPSs) from inverted moment tensors. In general, the full moment tensor inversion requires both P- and S-wave data from at least two observation wells. In cases where only a single observation well is available, the deviatoric moment tensor inversion can be performed first, the constraint of a zero-percent volumetric component, which is appropriate for pure shear source type, needs to be checked to ensure the reasonable FPS is obtained.
This paper briefly reviews the moment tensor inversion with application to microseismic fracture mapping and shows how to obtain the FPS from the inverted moment tensor. Examples from both dual- and single-array data are presented to show the application. Also, the potential effects of noise and eventlocation errors on the resultant FPS are discussed.
Introduction
Microseismic hydraulic-fracture mapping has become a valuable tool for monitoring fracture growth and behavior in unconventional reservoirs and provides information to help improve stimulation designs and achieve optimum recovery from the reservoirs. Basically, microseismic monitoring is the placement of seismic receiver systems in offset wells at a depth relatively close to a hydraulic fracture so that small earthquakes induced by the fracture can be detected and located to provide geometric and behavioral information about the hydraulic-fracturing process. When microseismic event locations are the only area of interest, most investigations focus on the impact of the velocity model, array geometry, acquisition parameters, noise, and data quality on location accuracy. With more attention now placed on attempting to extract additional information from those microearthquakes, new interest has focused on source parameters and source mechanisms (Nolen-Hoeksema and Ruff 2001; Jechumtálová and Eisner 2008; Rutledge et al. 2004; Šílený et al. 2009), such as the source type, source radius, slip amount, faultplane orientation and slip direction, etc. To solve these problems, investigators have been adopting technologies used in traditional seismology, such as moment tensor inversion, spectral analysis, etc. The primary information derived from moment tensor inversion is the slippage-plane orientation, the slip direction, and the moment. These slippages occur on existing planes of weakness, such as natural fractures, bedding planes, or potentially even fracture planes induced by the hydraulic fracture, thus providing information about the reservoir and the process. Extracting FPSs from the moment tensor can potentially be used as a reservoir characterization tool.
However, compared to traditional earthquake seismological source-mechanism studies, which use surface seismometers that record earthquakes from locations all over the world, the analysis of microseismic events obtained from downhole arrays during hydraulic fracturing is limited because of the minimal coverage of the focal sphere. In general, a downhole microseismic array is likely to be a vertical or horizontal array that is only several hundred feet long, providing a very small angular coverage of the seismic radiation from the event. As a result, care must be taken in both analyzing and interpreting source results from microseismic tests, and the limitations of the analysis need to be factored into any interpretation of such results.
In addition to the limited view of the microseismic event, the uncertainty in the velocity structure and effects of anisotropy and lithologic variability serve to complicate any analysis. Coupling of the receivers to the earth, either because of the clamping mechanism or cement quality, can also serve to modify the waveforms and thus reduce the accuracy of the analysis. Clearly, analysis of the source mechanism has not been as prominent a feature of microseismic monitoring as the event location because of this myriad of difficulties, but the potential for extracting some useful information that might characterize the fracture treatment, the reservoir, or the stress state still makes such an analysis worthwhile.
This paper discusses the application of moment-tensor inversion for extracting source information on microseismic data and shows how to obtain the FPS from the inverted moment tensor. Examples from both dual- and single-array data are presented to show the application. The comparison between the two-well case and single-well case shows that multi-well analyses will generally give better FPS results and are less affected by noise because the geometry is usually more conducive to extraction of these parameters, as reflected in the condition number parameter. This paper also demonstrates the effect of noise in the amplitude data and the event mislocation on the results of moment-tensor inversion and FPS.
Moment-Tensor Inversion
A moment tensor is a symmetrical tensor. It describes the general source type with six elements, and the source information can be deduced from any observed waveforms with longer wavelengths than the linear dimension of the source. The determination of the moment tensor involves an inversion of the moment elements, the observed amplitudes, and the propagation through the earth medium. In particular, the nth component of displacement as a result of a point source is represented as the convolution of a second-order moment tensor, Mpq, and the gradient of a Green’s function, Gnp,q (Aki and Richard 2002):

In this formulation, Gnp is the Green’s function, which describes the displacement at the receiver location caused by a unit pulse applied at the source location.
Moment-tensor inversion is a method used in traditional seismology to invert the amplitudes of P- and S-waves for earthquake source mechanisms, and most typically for cases where the seismometers are located on the surface. For oil-and-gas applications, the same methodology is being applied to microseismic monitoring of hydraulic-fracturing treatments, where geophone arrays are installed in an observation well. This receiver geometry has very limited focal coverage, which presents a challenge to investigators working on this problem. Vavryčuk (2007) showed that the complete moment tensors of seismic sources in homogeneous or vertically inhomogeneous isotropic structures cannot be retrieved using receivers deployed in one vertical borehole. They can be retrieved from amplitudes of P-waves, provided that receivers are deployed in at least three boreholes. Using amplitudes of P- and S-waves, two boreholes are, in principle, sufficient. Table 1, which is reproduced after Vavryčuk (2007), shows how many numbers of the recoverable moments can be obtained from the amplitude data from a certain number of observation wells.
In general, the least-square method is adopted, as in the standard seismological moment tensor-inversion, which is formulated as Gm=d and specifies how the amplitude data vector, d, is linked to the moment tensor through the formation’s Green’s function. However, there are different formulations regarding how to form the discrete Green’s function (G). The method used in this paper (Sokos and Zahradnik 2008; Warpinski and Du 2010) is to construct the Green’s function using six basic focal mechanisms. In this formulation, the sixth focal mechanism is the volumetric component, which simplifies the deviatoric moment-tensor inversion by excluding the sixth elementary mechanism from the inverse problem. This is the easiest way to reduce the number of unknowns from six to five to stabilize the inversion from single monitor well data. In later section it shows that the resulted FPS from deviatoric moment-tensor inversion from single monitor well data could be wrong for nonpure-shear source type. So it is very important to perform an additional QC check on the resulted moment tensor to make sure zero-trace (zero percent of volumetric component) is satisfied, otherwise the results have to be discarded.
Once the best-fit moment tensor is obtained, the moment tensor is normally decomposed into three components (Vavryčuk 2001): double couple (DC), compensated linear vector dipole (CLVD), and isotropic (ISO).
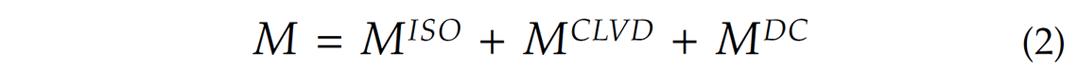
| Waves | 1 Well | 2 Wells | 3 Wells or More | |
|---|---|---|---|---|
| TABLE 1—NUMBER OF RECOVERABLE MOMENTS (AFTER VAVRYČUK 2007) |
||||
| P | 3 | 5 | 6 | |
| S | 4 | 5 | 5 | |
| P and S | 5 | 6 | 6 | |
Moment-Tensor Decomposition to FPS
The general expression of a symmetric moment tensor is represented as (Dufumier and Rivera 1997)
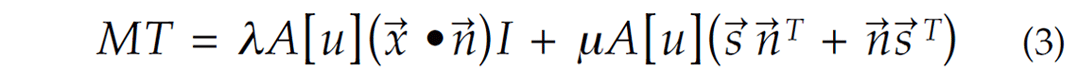
where λ and μ are Lame’s constants, A is the area, the scalar [u] is the displacement discontinuity, n→ is the normal vector, and s→ is the slip vector. The normal and slip vectors can be interchanged for any data set and thus represent the normal directions of two possible fault planes. They are called FPSs in this paper.
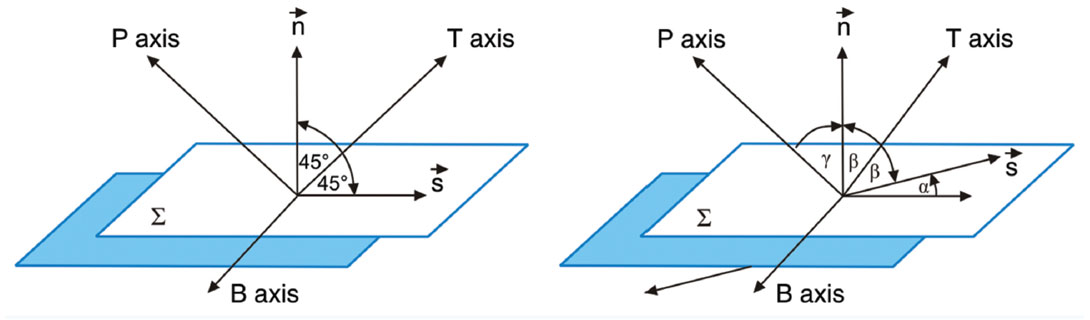
The P (pressure axis), T (tension axis), and mutually orthogonal B axis are the principal direction of the moment tensor. The angle (α), defined as the angle between the slip direction and fault plane (Figure 1), can be calculated from the eigenvalues of the deviatoric moment tensor (Dufumier and Rivera 1997; Warpinski and Du 2010). The relation between these principal axes and the normal and slip vectors are illustrated in Figure 1. This indicates that, once the moment tensor is obtained through inversion and eigen-decomposition is performed on the moment tensor, the FPS (normal and slip vectors) can be obtained.
Examples
Two examples are presented to demonstrate the application of moment-tensor inversion and FPS. Also, the potential effects of noise and event-location errors on the resultant FPS are discussed.
1). Moment-Tensor Inversion from Two-Well Data
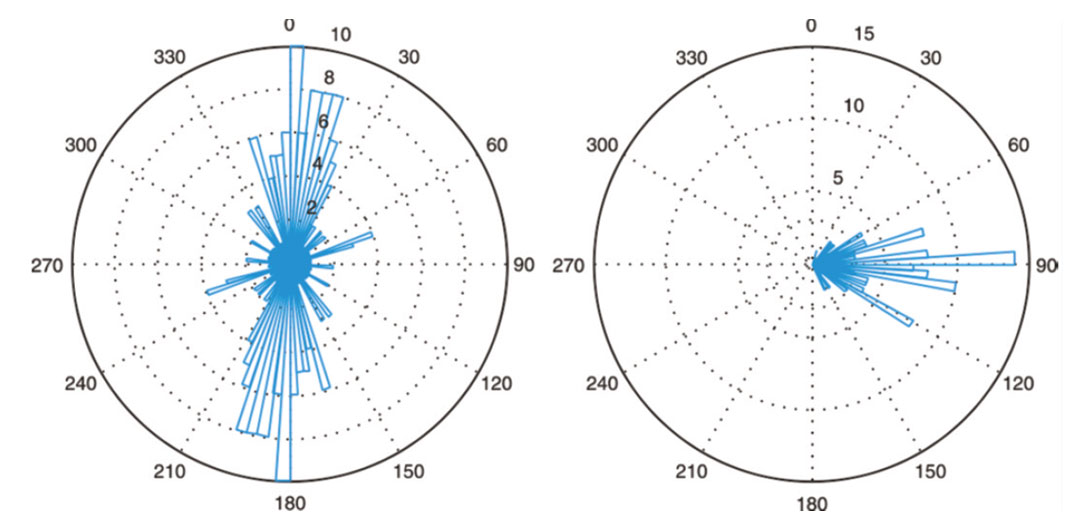
The first example is a case in the Barnett shale where two monitor wells approximately 450 m apart were used to monitor large-volume stimulations in a horizontal well at depths of about 2,100 m (Warpinski and Du 2010). Both monitor wells had 12 receivers spaced 12 m apart, with the tools situated just above the shale interval that was being stimulated. A plan view of the geometric configuration is shown in Figure 2. Only a few selected high-quality events are shown in Figure 2 to minimize errors associated with noise and data quality. As with many of these gas-shale reservoirs, the velocity structure is complicated by very fast carbonates adjacent to the shale, resulting in complex ray paths, refractions and reflections, and a smaller than usual coverage of the focal sphere. After these microseismic events with high quality of data were selected, their amplitudes were determined and inverted for moment-tensor components and fault information. Figure 3 shows the fault-plane strike and dip angles as resolved from the moment-tensor inversion and subsequent analysis of the eigenvalues and eigenvectors to determine fault planes. The right-hand side shows the dip angles, indicating that most of the slippages are occurring on nearly vertical planes. More interesting is the plot of the strike angles, which shows a primarily NNE direction, although these results are consistent with fracture analyses obtained by Gale et al. (2007). This rose diagram shows both of the possible fault planes, but the expected bimodal distribution is not observed. The reason for this is that the inversion resolves relatively large magnitudes of α for most of these events so that the fault plane normal and slip direction are not very different.

2). Moment-Tensor Inversion from Single-Well Data
As shown in Table 1, only five out of six elements of the moment tensor could be resolved when only single-well data (both P- and S-wave) is available. Constraint needs to be added in the inverse problem to stabilize it. The constraint adopted here is the zerotrace constraint (or zero percent of volumetric component), which is essentially a modified deviatoric moment-tensor inversion with additional QC criterion applied on the trace of the resulted moment-tensor.
In the synthetic case (Warpinski and Du 2010), a tool string with 12 sensors is placed in the center of a ring of microseismic events. The sensors are located at depths from 1,500 to 1,650 m and all microseisms are at a depth of 1580 m and a distance of 150 m, spaced 30 degrees apart. Three separate pure-shear configurations are run: a vertical plane oriented north-south with strikeslip motion; a vertical plane oriented east-west with dip-slip motion, and a vertical plane oriented north-south with dip-slip motion. Because the two directions (fault-plane normal and slip) in a pure-shear case can be interchanged and still produce the same radiation pattern, these three cases are respectively equivalent to a vertical plane oriented east west with strike-slip motion, a horizontal plane with north-south slip, and a horizontal plane with east-west slip. The synthetic case demonstrates that the FPS could be resolved using single-well data for pureshear type source (α = 0°) by performing the deviatoric momenttensor inversion. However, for nonpure-shear source types (nonzero α, where the fault plane is the north-south direction and the slip vector is α away from the plane), if only single-well data are used, the resulting FPS could be wrong. The larger the angle α is, the more the resultant strike angles deviated from input values (Table 2).
| α (degree) | ISO (%) | DC (%) | CLVD (%) | Max Error on Strike (degree) |
|---|---|---|---|---|
| TABLE 1—NUMBER OF RECOVERABLE MOMENTS (AFTER VAVRYČUK 2007) |
||||
| 0 | 0 | 100 | 0 | 0 |
| 5 | 12.4 | 77.7 | 9.9 | 12.5 |
| 10 | 21.5 | 61.3 | 17.2 | 26.9 |
| 15 | 28.4 | 48.8 | 22.7 | 45.0 |
3). Effect of Noise in the Amplitude Data and Event-Location Error
For any geophysical inverse problem, it is very important to quantify the uncertainties of the inverted parameters. For moment-tensor inversions, the least-square solution is usually implemented, where standard methods, such as the covariance matrix method (Menke 1989), can be used to quantify the uncertainties of the inverted moment tensor. However, propagating the uncertainties of the moment tensor into the FPSs (fault plane orientations) is much more difficult because it involves solving the eigenvalues and eigenvectors of the moment tensor to obtain the orientations of the fault plane, which is a highly nonlinear problem. Du and Warpinski (2011a) examined the uncertainties of fault plane orientation caused by the noises in the amplitude data using an extended analytical method and the Monte-Carlo method. The results showed that the uncertainty of α is larger than the uncertainties of the strike and dip angles. The uncertainties of α strike and dip angles all increased with increasing angle α.
Du and Warpinski (2011b) examined the effect of the event-location error on the resultant FPS using a two-well monitoring example. In this example, two vertical tool strings with 12 sensors each are placed at (0, 0) and (300, 0) m, as shown in Figure 4. The sensors are located at depths from 1,450 to 1,600 m. All the microseisms have the same strike-slip source type, where the fault plane is vertical and oriented at N45°E, with the slip direction on the plane and along the strike direction. For pure strike slip, the angle α and the volumetric component percentage of the moment tensor are zero. Because of the interchangeability of the fault-plane normal and slip direction, with this geometry there are two FPSs that are both vertical. One FPS is the original vertical fault oriented in N45°E direction; the second one is the auxiliary plane, which has the slip direction as its normal direction at N45°W.
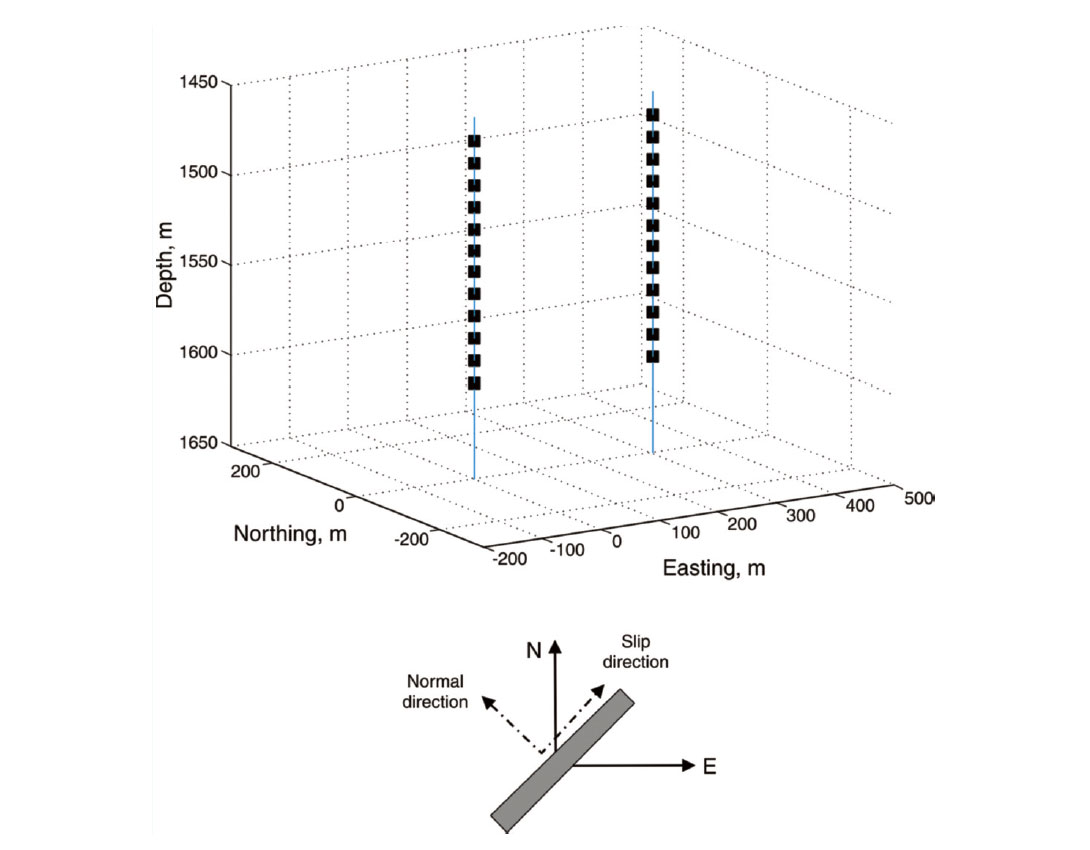
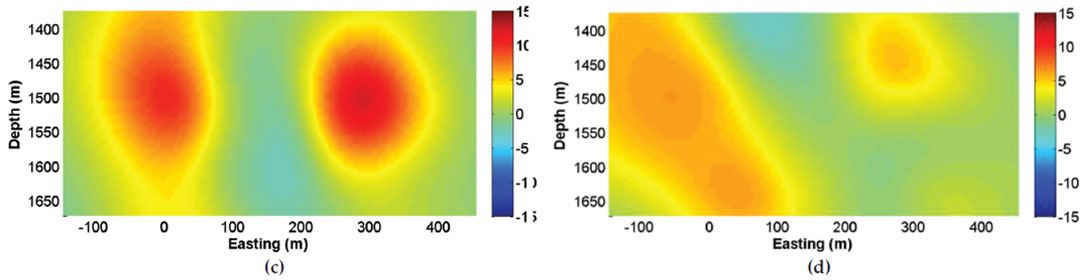
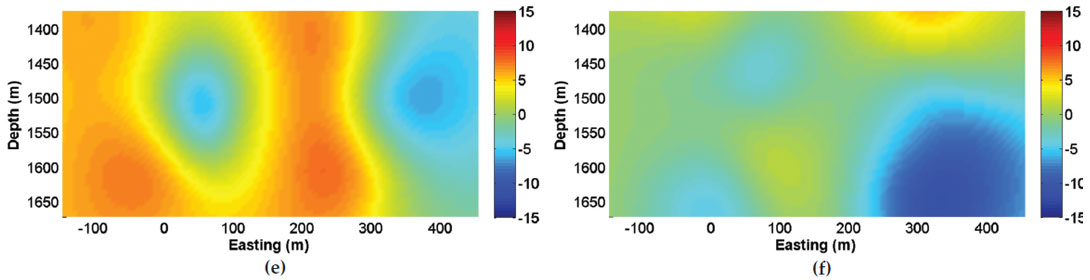
Given the geometric setup shown in Figure 4, we examine the effect of event-location error on the inverted moment tensor and FPS by calculating the solutions over a grid of points on the Easting-Depth plane with a constant Northing value of 150 m. The synthetic amplitude data at the two observation arrays are generated for each grid point on the plane, and moment-tensor inversion is performed using the perturbed event location on the grid, which has 15 m of location error in each direction in this example. The results are given in Figure 5. Figure 5a shows the distribution of the condition number, which is defined as the ratio of the largest to the smallest singular value of matrix G (Dufumier and Rivera 1997) on the Easting-Depth plane. The condition number controls the stability of the inversion process; in general, a smaller condition number signifies a more stable inversion and better solution. The distribution of the angle α is shown in Figure 5b, where it can be seen that there are both positive and negative α angles distributed over the Easting-Depth plane. Depending on the event location, its uncertainty could cause positive and negative α values in the inverted FPS results, which indicates there is a nonzero explosive or implosive volumetric component in the retrieved moment-tensor solution. These results suggest that some or all of the nonpure-shear (non- DC) source type that is in the FPS obtained from the momenttensor inversion could be caused by the event-location uncertainty. The errors in the strike and dip angles for the two FPSs induced by the event-location error are shown in Figures 5c to 5f, where it can be seen that the errors are relatively small for events located in the middle portion of the area on the plane (with the Easting around 150 m) but get larger as event locations extend to other areas. This is consistent with the conditionnumber plot (Figure5a), where the condition numbers in the middle portion of the area on the plane are smallest, which indicates that the solution in those areas are generally better and more stable.
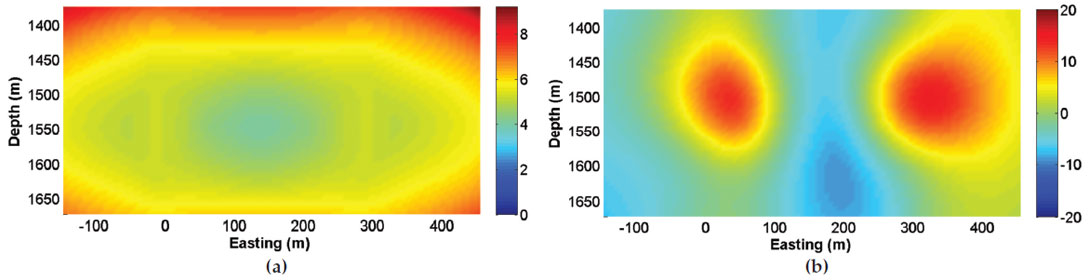
(a) Condition numbers.
(b) Resultant angle alpha.
(c) Resultant strike-angle difference from input strike angle of FPS in NE direction.
(d) Resultant dip-angle difference from input dip angle of FPS in NE direction.
(e) Resultant strike-angle difference from input strike angle of FPS in NW direction.
(f) Resultant dip-angle difference from input dip angle of FPS in NW direction.
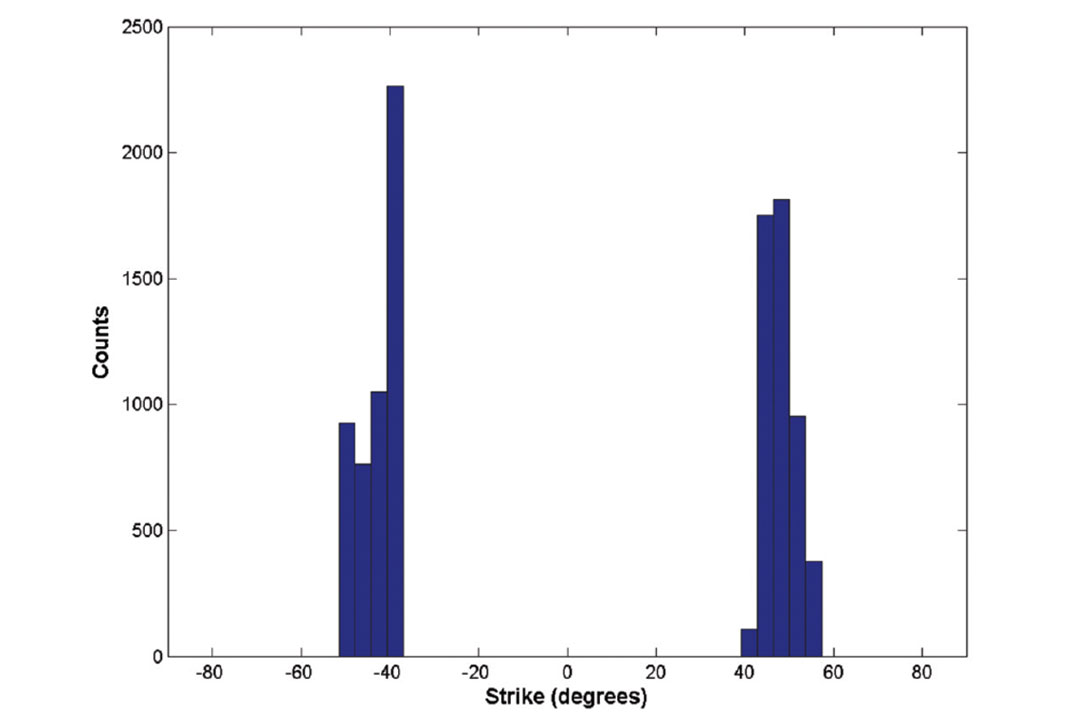
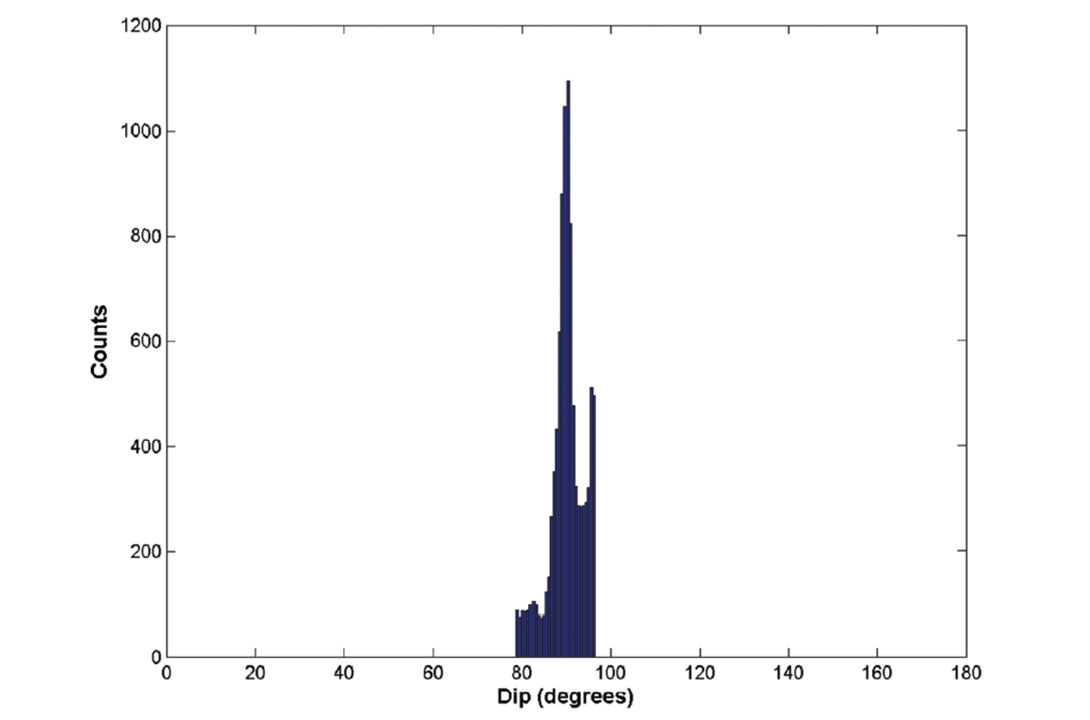
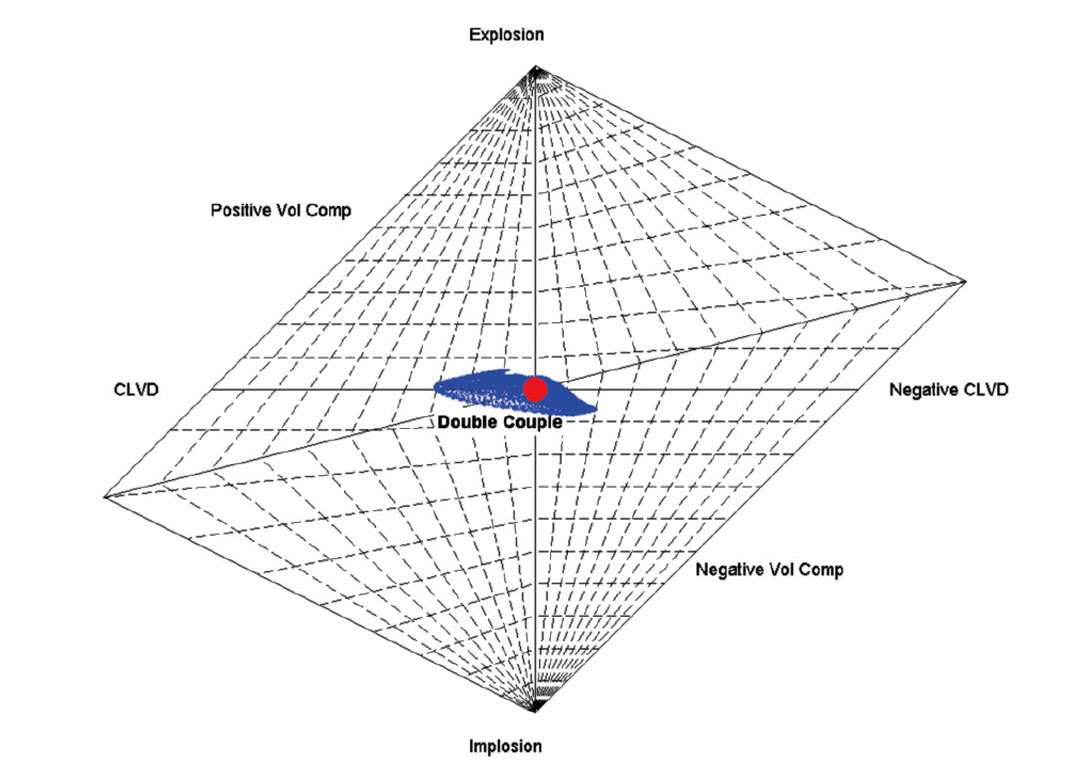
Another way to look at the effect of event-location uncertainties on FPS is to plot the resultant FPS angle distribution and the Hudson T-K source-type plot in Figure 6 for the two-well synthetic example. Figures 6a, 6b, and 6c show the histogram of alpha, strike, and dip angles for all the events on the plane caused by event location uncertainty. We can see their distributions are relatively tight around their input values, compared to the broad spatial distribution of differences on the Easting-Depth plane shown in Figure 5. Figure 6d shows the Hudson T-K source type for all the inverted moment tensors with mislocated events on the plane, which has all the moment-tensor solutions situated in a tight region around the input pure shear (double-couple) centered in the T-K source plot.

(a) Histogram of alpha angles.
(b) Histogram of strike angles.
(c) Histogram of dip angles.
(d) Hudson’s T-K source-type plot (the red dot in the center is the input moment tensor for a pure double-couple source).
Discussion
An FPS can be extracted from the inverted moment tensor. Mathematically performing the deviatoric moment tensor inversion is enough to extract the FPS, as the angle α, which is defined as the angle between the slip direction and the fault plane, is only a function of the eigenvalues of the deviatoric moment tensor, and fault normal and slip directions are a function of the angle α and the eigenvectors of the moment tensor, which are the same as the eigenvectors of the deviatoric moment tensor. This means that the FPS can be extracted using the deviatoric moment-tensor inversion from single-well data, even for nonpure-shear source types. However, there are sampling errors that might be inherent in the single-well case, caused by the limited coverage on the focal sphere, that would potentially prevent doing so using single-well data for nonpure-shear source type.
These results also show that care needs to be taken whenever FPSs are generated through moment-tensor inversion. There are many sources of noise, such as receiver resonances, flow noise, nearby drilling, wellbore leaks, and others that can potentially cause significant errors in the results and in the final interpretation. In addition, mislocation of the microseismic events, either because of incorrect arrivals or insufficient velocity models, is a potential source of error and uncertainty.
Conclusions
Moment-tensor inversions of microseismic data can yield information about both the slippage planes (fault planes) and the microseismic mechanism. In this paper, we discussed the moment-tensor inversion and FPS using microseismic data from linear observation arrays. With two monitoring wells, the full moment tensor can be determined. With only a single monitor well, only the deviatoric moment tensor is retrievable, which limits the amount of information that can be extracted. Reliable single-monitor-well inversions are likely to be those where the value of α is very small, implying that the results support the assumptions (no volumetric component).
We also examined the effect of noise in the amplitude data and the event location errors on the resultant moment tensor and FPS. The results showed that the uncertainty of angle α is larger than the uncertainties of the strike and dip angles. The uncertainties of α, strike, and dip angles all increase with increasing angle α. Also, the event-location error could result in an interpreted non-DC (nonzero α angle) mechanism for a true pureshear (DC) source type.
The condition number controls the stability of the inversion process; in general, a smaller condition number signifies a more stable inversion and a better solution. The condition number can also be looked at as a factor that controls the magnification of data uncertainties to model uncertainties. For each microseismic monitoring survey, when the initial velocity model is provided, the condition numbers can be used in prejob-design studies to identify areas where a stable moment-tensor solution could be retrieved.
To summarize, to perform moment-tensor inversion and obtain reasonable FPS results, the rules need to be followed:
- Identify high-quality microseismic data with large signal-tonoise ratio.
- Perform moment-tensor inversion on the events with little location uncertainty.
- Look at the results from moment-tensor inversion and FPS statistically.

Acknowledgements
The authors would like to thank Halliburton for permission to publish this paper.











Join the Conversation
Interested in starting, or contributing to a conversation about an article or issue of the RECORDER? Join our CSEG LinkedIn Group.
Share This Article