Science Break: The Physics of Golf

With golf season upon us, it seems like a perfect time to look at some of the physics behind golf. This is a well understood and extensively covered topic, probably because there are so many golfers, and the game is just so darn confounding, confusing and challenging. Many, many interesting articles and links can easily be found on the Internet by searching on “physics of golf”.

With golf, it’s all about the spin of the ball. Almost everything interesting that can happen, whether good or bad, is connected in some way to the spin of the ball.

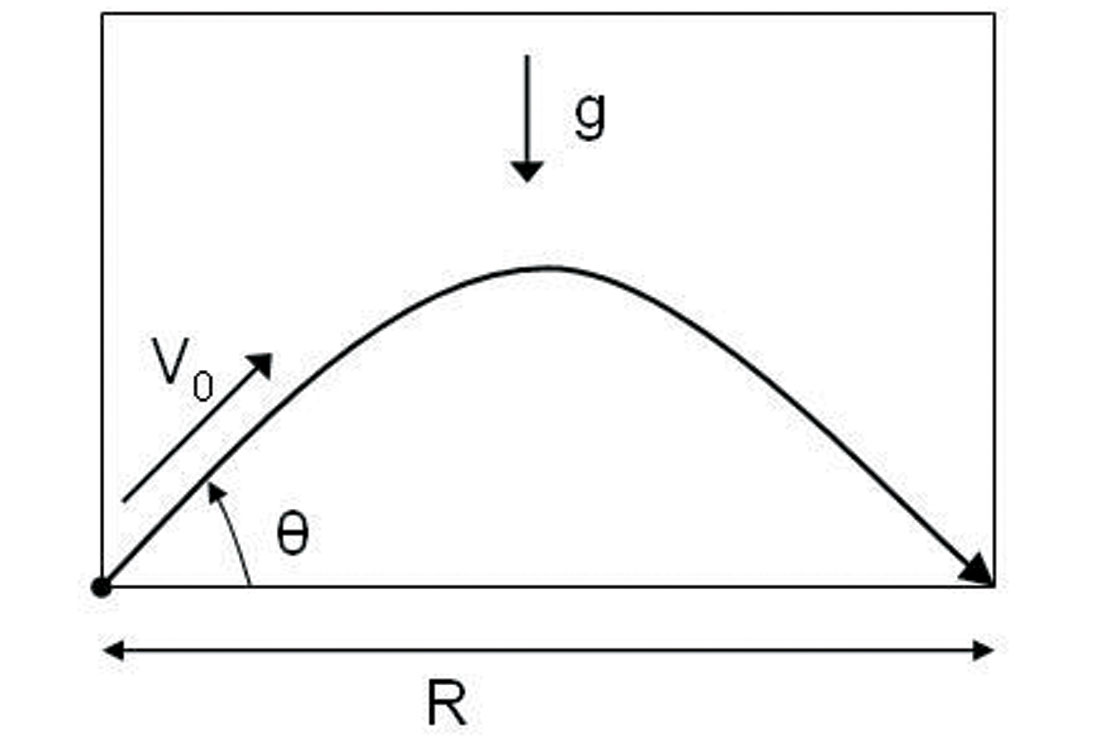
Classic Newtonian mechanics tells us that the range of a projectile is described by the following equation (and Fig.1):

R = (V₀²sin2θ) / g

R is the range, the distance between launch point and landing point,

V₀ is the launch velocity,

θ is the launch angle,

and g is the force of gravity, 9.8 m/s².

Given that the force of gravity is downwards, it follows that the launch angle that gives the greatest range, all other variables remaining equal, is 45 degrees. Yet the golf club that propels a golf ball the greatest distance, a driver of some sort, is generally launching the ball at a much lower angle than 45 degrees, perhaps between 10 and 20 degrees. How can this apparent disagreement between basic physics theory and observation be explained? As you might have guessed, it’s all related to the spin of the ball, and the fact that most golf courses aren’t located in a vacuum (the equation applies only to a situation where there is no air resistance).

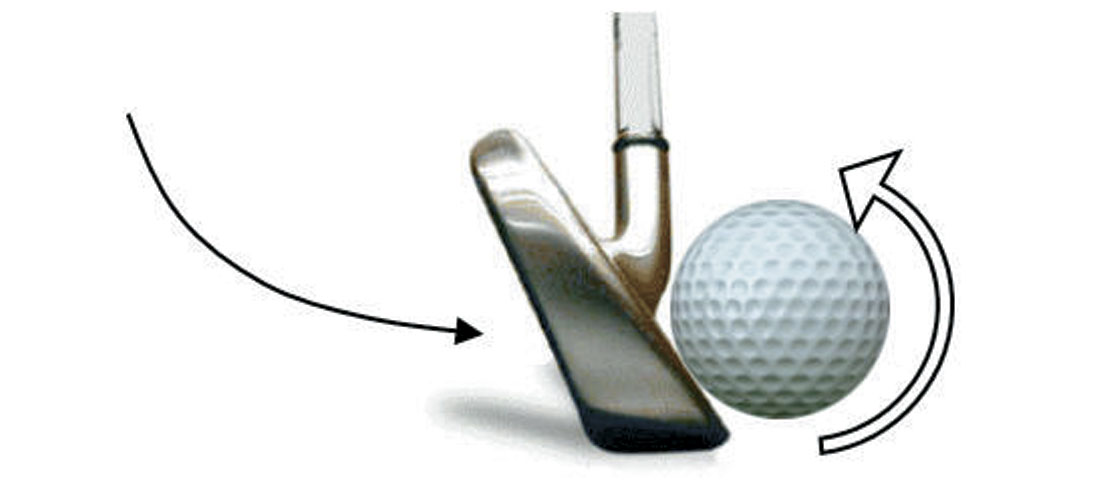
There are actually two interesting effects at play. (To be honest, it is unclear to me whether these are two distinctly separate effects, or different ways of describing and understanding the same phenomenon. Any comments from readers to shed further light on this topic are welcomed.) The first is one any scientist is very familiar with, and that is the Bernoulli effect. When the angled club face strikes the ball (Fig. 2), it imparts a back spin on the ball. At the top of the ball, the backwards spin of the ball drags a thin layer of air with it, adding to the air’s relative velocity. At the bottom of the ball the situation is the reverse – the spin of the ball is against the flow of the air rushing past, so the thin layer of air near the ball slows down the flow of air past the ball. Hence we have a situation very similar to that of an airplane wing, with air flowing over the top of the ball faster than that flowing under the ball. As we all know, this creates more pressure under the ball, and thus upward lift.

As the spinning ball travels through the air, it experiences another effect known as “Magnus lift”. This Magnus effect is caused by differential drag occurring above and below the ball. Again, at the top of the ball the spin is backwards, with the flow of air, so there is less drag created by the motion of the ball relative to the surrounding air; the turbulent layer (known as the boundary layer) is relatively thin. At the bottom of the ball the situation is the reverse – the ball is spinning forwards in the direction the ball is moving, hence there is more drag; the turbulent boundary layer is thicker than at the top. This situation of differential drag also imparts lift on the ball, adding to the Bernoulli effect.

The contribution of these two lift forces, which aid in driving the ball as far as possible, is maximized at lower launch angles. If the launch angle is too high, say 45 degrees or higher, then a large component of the lift experienced by the ball is actually backwards rather than up. This can send the ball into a steep ascent, making it fly far higher than necessary, and it will drop to the ground well short of its maximum range.

Because of the Bernoulli and Magnus effects, the flight path of a golf ball is not the perfect parabola described by the equation. Instead, at the beginning of the ball’s flight, when velocity and backspin are at their maximum, lift is also at its maximum. So the parabolic curve is straightened out, even to the point (with some powerful hitters) where the ball’s path may be curving upwards a bit. As the ball slows down and spins less, the effects of wind resistance and gravity become more dominant, and the ball reverts to a downward path more akin to a parabola, and it drops more and more steeply to the ground.

You often hear that the dimples on a golf ball actually reduce drag, allowing the ball to fly farther. True and not true. The dimples do allow the ball to fly farther, but this happens because of two effects. First, the dimples increase drag in a way that enhances the Magnus effect, and second, they decrease drag associated with the “wake” the ball leaves behind it as it passes through the air.

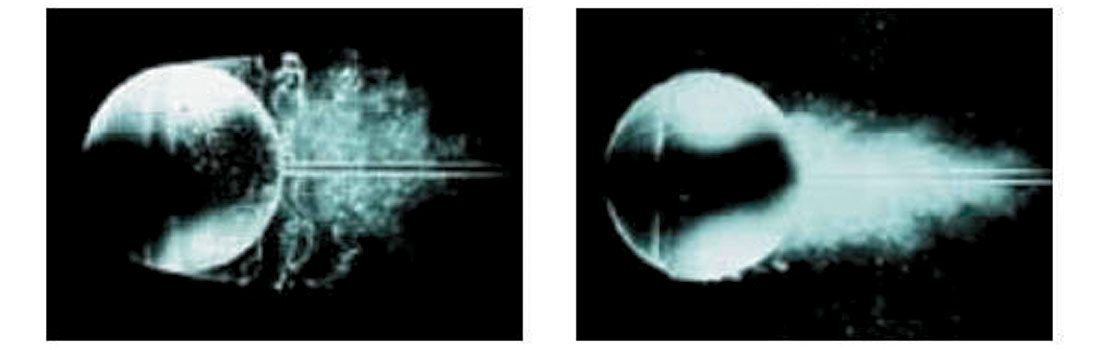
The flow of air around a body, in this case a golf ball, can be described as being either laminar (smoothly flowing) or turbulent. Smooth balls tend to experience laminar air flow a round them; balls with rougher surfaces tend to experience turbulent air flow around them. Turbulence is associated with drag and pressure. For the Magnus effect to play a role in allowing a golf ball to fly further, there need to be zones of turbulence both above and below the ball. The dimples do this, creating turbulent boundary layers above and below the ball at much lower velocities than with a smooth ball.

The second dimple effect is also related to turbulent versus laminar air flow past the ball, and is beautifully illustrated by figure 3. Laminar air flow (as with a smooth ball) will tend to separate from the surface of the ball much sooner than turbulent flow, leaving a large wake. Turbulent flow (as with a dimpled ball) tends to “stick” to the surface of the ball longer, resulting in a reduced wake. So while the dimples create turbulence at the front, top and bottom of the ball that actually increases drag, thus slowing the ball down, they more than compensate for this by reducing the size of the wake, thus reducing drag from behind the ball, and resulting in a net reduction in drag compared to a smooth ball.

The twin curses of most average golfers, hooks and slices, are simply manifestations of the same Magnus and Bernoulli effects. The difference of course is that instead of purely vertical spin, some flaw in the golfer’s swing imparts a horizontal component to the spin on the ball. A top notch golfer tends to hit the ball with a square club face, thus keeping the ball spin in the vertical plane. A less accomplished golfer tends to hit the ball with an angled club face, either angled inwards (a hook) or outwards (a slice). This angle of the club to the ball imparts a sideways component of spin, sometimes referred to as the gear effect. Thus instead of the ball experiencing purely upwards lift, it is also pushed to either the left or the right. Viewed from above, if the spin of the ball is clockwise, it will tend to veer to the right (Fig. 4); if the spin is counterclockwise, it will of course veer to the left.

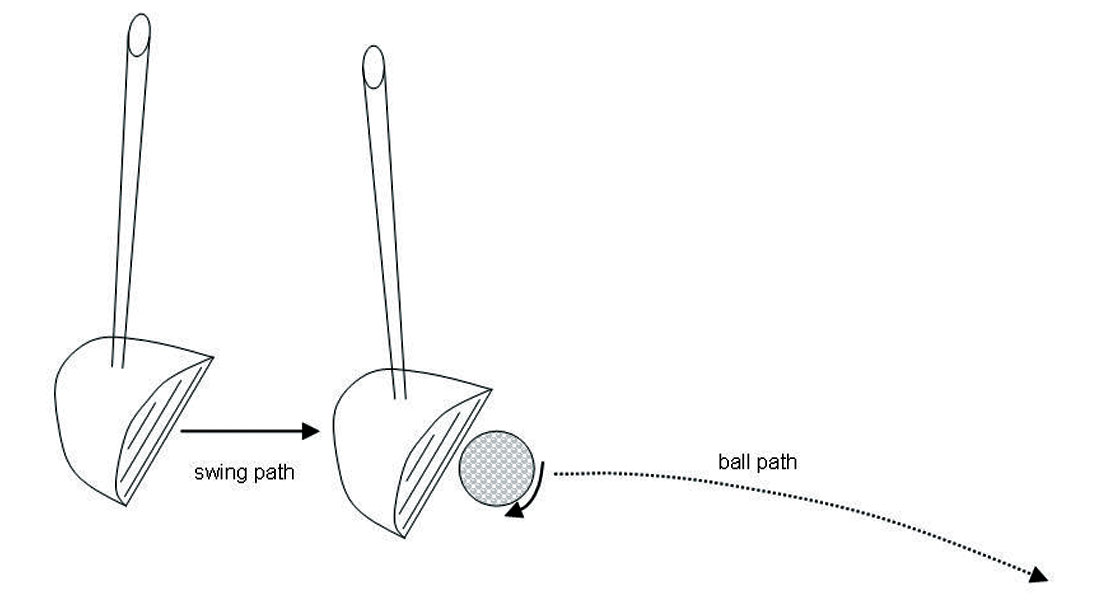
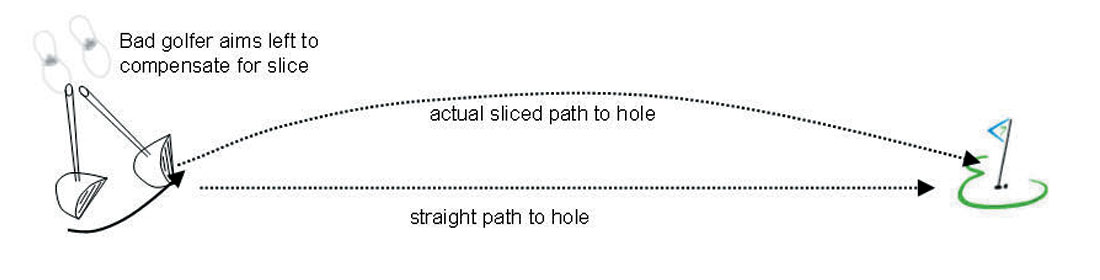
Most higher handicap golfers have a tendency towards either a hook or a slice. Usually over time they develop compensations for their bad swing habits. Instead of aiming straight at the hole, they aim either to the right or left of it, anticipating a curved ball flight (Fig. 5). At the first Doodlebug I attended I won a KP (closest to the pin) prize. Luckily very few people saw the actual shot – I aimed the ball well out over the Bow River, and my awfully reliable slice cooperated, bringing the ball back over land, to bounce on the green and roll within a few inches of the cup.

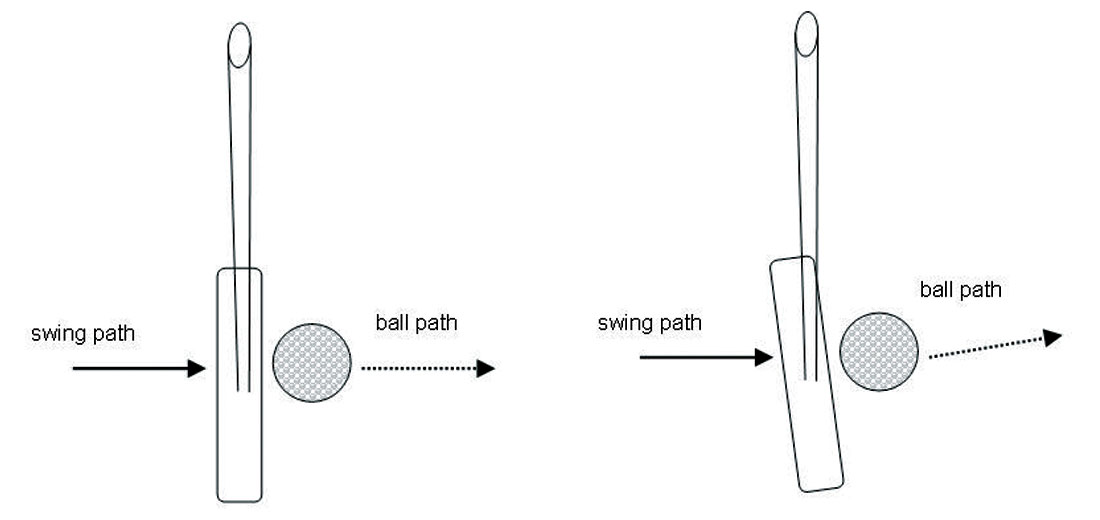
With putting, the low speeds and spins render the Magnus and Bernoulli effects insignificant. However, if the ball is struck with a non-square club face, the ball will not travel along the desired path to the hole. Instead, it will leave the club face at an angle described by simple vector mathematics (Fig. 6). Of course this effect is also at play with the longer driving clubs described above, adding to spin-induced hooks and slices. Another confounding factor with putting, often overlooked, is the effect of the dimples. Within the relevant scale, the face of the putter is flat, but the localized surface of the dimpled ball that the putter comes in contact with is definitely not. There is a certain randomness at play, in that the dimples themselves may cause the ball to leave the club face at a small angle off of normal. The range of variability introduced by the dimples has been estimated at close to 1 degree, which is certainly significant for longer putts.

There are of course many other parts of the game of golf that are very interesting to analyse using the science of physics. Some of these would include the effect of different ball compositions and structures on spin and velocity, the mechanics of the golf swing, the effect of shaft stiffness and club head composition, the use of mild hook and slice (draw and fade) to achieve desirable results, etc., etc. But just looking at the physics of ball spin, as briefly touched on here, is a large topic in itself. Once the basic physics of golf ball spin are understood, they are easily applied to all the other ball sports. Of particular interest to me are the different spin effects that can be applied to a tennis ball (for example, tennis topspin achieves the exact opposite of golf ball backspin: i.e, drives the ball to the ground as quickly as possible— thereby allowing the player to hit the fastest possible shot that still falls within the court), and the unbelievable ball action techniques used by baseball pitchers and cricket bowlers to bamboozle batters.