Seismic exploration in areas of rugged and extreme topography is dangerous, difficult and expensive. Because of these environmental and economic factors it is not uncommon for data acquired in such areas to be inadequately sampled in space for imaging purposes. Also, long source-receiver offsets are often required in order to detect the returning reflected energy from the steeply dipping subsurface geology. These long offset distances, combined with steep topography and fast outcrops, can result in high emergent angles from the vertical at the receiver.
The recent introduction of various autonomous recording systems (for simplicity referred to as nodes in this text) and the ability to use 3C sensors with such nodes have the potential to overcome some of the problems mentioned above. In the following, the influence on the quality of seismic images in such challenging areas resulting from the improved data acquisition techniques now enabled by these technologies will be discussed.
Methodology
The spatial sampling requirements for unaliased data acquisition and imaging are directly proportional to velocity and inversely proportional to the propagation angle and maximum frequency. In extreme topographic environments the rocks tend to have fast seismic velocities, even at the surface, which leads to a loosening of the requirement for spatial sampling. The maximum attainable frequency seems to be quite low in such environments, which also leads to a looser requirement for spatial sampling. This loss of high frequency seems to be common in Foothills areas, even for 2D lines that would seem to be adequately sampled in space. On the other hand, dips will be high with considerable potential for overturned bedding, and this leads to a tighter requirement for spatial sampling. Depth is not a factor in spatial sampling but, as velocities tend to increase with depth and the maximum frequency decreases with depth, the spatial sampling requirement is generally tighter for the shallow section than for the deep section. The targets in topographically rugged areas often tend to be quite deep.
The spatial sampling is generally achieved through the surface interval between source points in one direction and receiver points in the orthogonal direction. Symmetric sampling (Vermeer, 1998) requires the source and receiver intervals to be equal to each other. This approach avoids any assumptions about the underlying geology and appears to be beneficial from data conditioning and image viewpoints. In most topographically rugged areas the notion of dip and strike directions is inadequate though these have been invoked in designing 3D surveys. There may be less dip in some directions than in others but there will be dip in all directions, further supporting the symmetric sampling concept that makes no a priori assumptions. However from the viewpoint of economics, source intervals almost always exceed receiver intervals, and economics also tends to dictate that the actual spatial sampling will be less than desired. Consequently, 3D surveys in these challenging areas are too frequently much more poorly spatially sampled than required. Given these circumstances it may be worth considering randomizing the spatial sampling, perhaps using the principles of Compressive Sensing (CS) (Herrmann 2010).
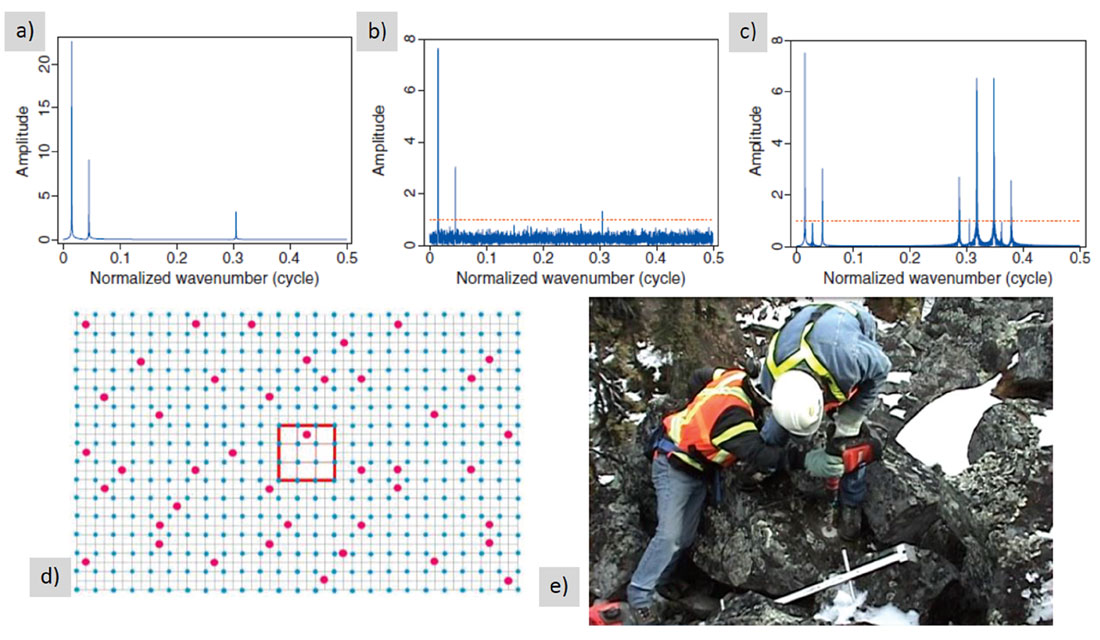
It is difficult to achieve random sampling with cable-based recording systems but quite easy with node-based systems. Truly random sampling is not required or even desired since this could lead to large areas so poorly sampled so as to make signal recovery impossible. Figures 1a, 1b and 1c, taken from Herrmann (2010), show the wavenumber spectral representation for three spatial frequencies sampled firstly uniformly and unaliased (1a), then randomly using CS rules (1b) and finally, uniformly and aliased (1c). There are an equal number of samples in Figures 1b and 1c but arranging these samples to perform compressive sensing turns the aliased signal into a low-level background noise in the wavenumber domain. This effect has also been demonstrated on actual field data by Mosher et al. (2012). Jittered sampling, where locations may be occupied within a certain area with equal probability, is a technique for ensuring that no large areas exist without being sampled reasonably well. An example of jittered sampling is shown in Figure 1d; taken from a paper by Milton et al. (2011). In this example a shot, in red, may occupy any of the nine squares outlined in red with equal probability; the blue dots are receivers on a regular grid in this instance. Perfectly regular grid sampling will often require placing sources and/or receivers in unsuitable locations as illustrated in Figure 1e. In this instance a sensor is being placed, at considerable effort, into a boulder that is on top of several other boulders and thus causing very poor coupling with the earth’s actual surface beneath the boulder field. In many instances there will be more suitable locations nearby that would offer better signal from either the receiver (or a source) at less cost and with less risk. This implies that there will be operational benefits in relaxing the demands for perfect grid locations. The more important criterion for receivers, and sources, is to maintain an adequate areal density while ensuring no gaps are too large. It should be feasible not only to achieve this with nodal systems but also to obtain longer offsets in all azimuths to provide data better conditioned for imaging.
Obtaining an image in the shallow section is frequently a problem in topographically rugged areas. The major reason for this is the interval between source and receiver lines. These are often farther apart than desirable, again for economic reasons. As with source and receiver intervals it is generally desirable that these be equal for symmetric sampling. However, as dynamite is most frequently the source and is often heli-portable, sources are considerably more expensive than receivers. There may thus be a case to use tighter receiver line intervals than source line intervals; this can be achieved while maintaining an even fold. It is important to obtain shallow images of reasonable quality in order to obtain shallow velocities for pre-stack depth migration; errors in the shallow velocity field will propagate as errors in the deeper image. Again, the use of a nodal system may enable a more economic and safe way of achieving tighter receiver line intervals.
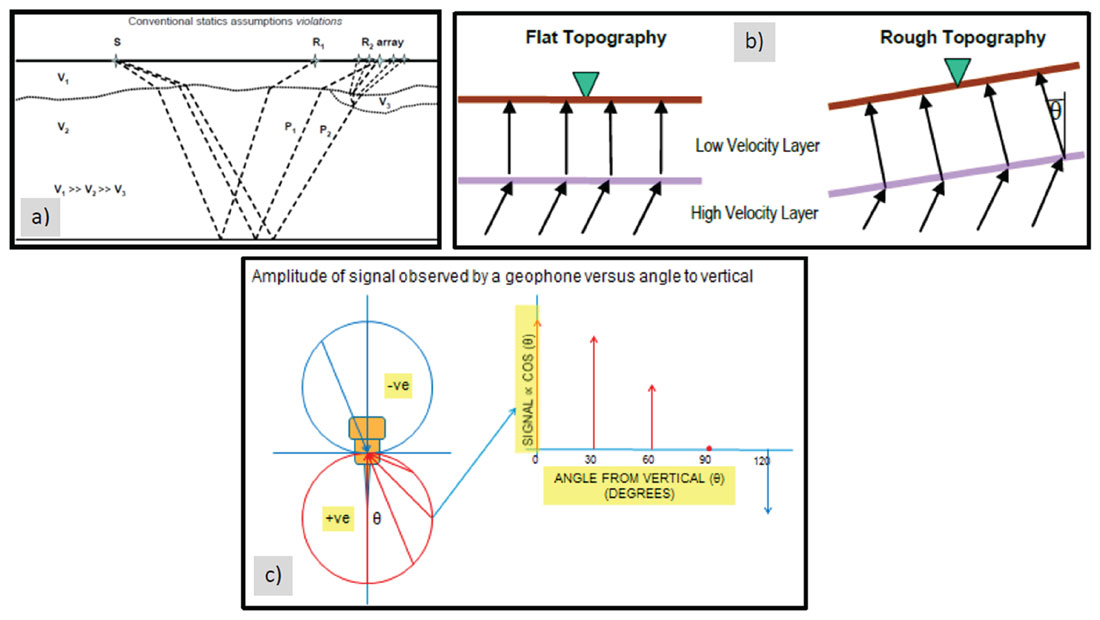
The most commonly used receiver in mountainous areas by far is the moving-coil geophone. This has a velocity signal output that decays with the cosine of the angle from vertical at which the energy arrives. The emergent angle from the vertical can be quite large where there is either little weathering at the surface or a hard fast rock at the surface such as an outcrop, as shown in Figure 2a (Henley, 2006), or for rugged topography as shown in Figure 2b (Behr, 2005), and for very long source-receiver offsets. This effect leads to a reduction in amplitude of the reflection signal as shown in Figure 2c (Maxwell, P., 2014 – internal communication) plus the potential for increased signal distortion should this angle be very large. Surface consistent amplitude processes will not compensate for this type of amplitude loss as it is not a surface-consistent effect but an arrival angle-consistent effect.
Given the above situation there are potential benefits to be gained by using 3C receivers, in order to obtain an improved P-wave image (rather than necessarily considering converted waves). With a 3C sensor of any type it will be possible to image the P-wave reflection without loss, regardless of the signal’s emergent angle at the sensor as the full wavefield is recorded.
Results
Two models were used to demonstrate the improvements in imaging to be gained from the use of longer offsets and improved spatial sampling plus the lost P-wave energy that may be recovered through the use of 3C sensors. For simplicity the models are 2D only but the results may be generalized to 3D. Compressive sensing was not modelled at this time but has been shown to be effective (e.g., Herrmann, 2010 and Mosher et al, 2012).
The first model used was the, by now famous, foothills model generated by MacLean et al (1996), identified in this paper as Model94. Elastic-wave source modelling was performed keeping all traces live and imposing a 12.5 km migration aperture rather than the 5 km limit used in the original modelling. The resultant data were then depth imaged with an elastic-wave RTM algorithm using the exact P-wave velocity for both the vertical and the horizontal components.
Figure 3 shows the resulting images for the vertical and radial components of the elastic wavefield after imaging with the P-wave velocity field. These images were processed through noise attenuation and image enhancement using the technique described in Khalil et al (2014). It is clear in these images that there is a considerable amount of PP energy on the radial (inline horizontal) component of the recorded data. This energy, evident on the more steeply dipping and shallow events, will be lost if only a moving-coil vertical geophone is deployed in the acquisition. Furthermore it is likely that energy arriving at a substantial angle from the vertical at a moving-coil geophone may suffer some distortion in the output signal; this will be a function of the manufacturing details of the geophone but is unlikely to be totally absent. Thus the PP energy shown in Figure 3 is likely better than what would actually be recorded by a moving-coil vertical geophone.
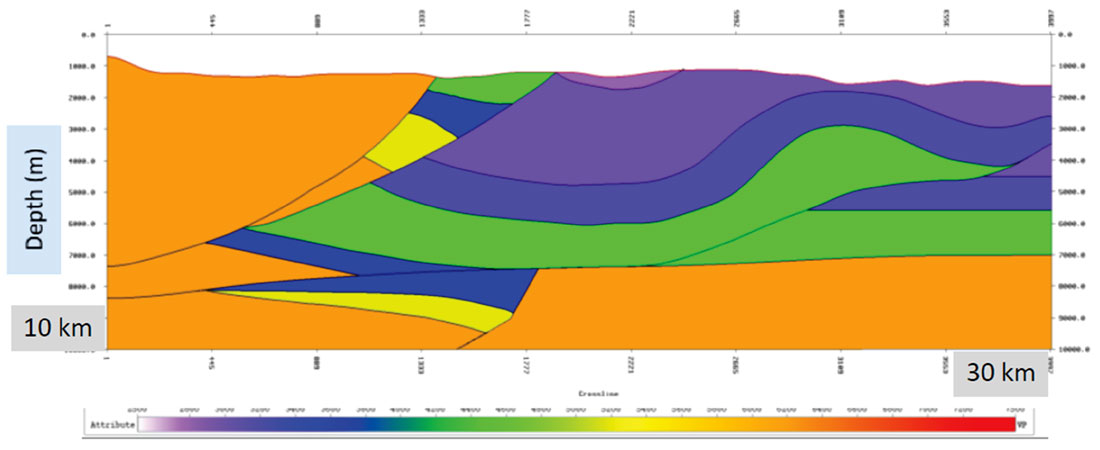
The second model, Figure 4, was created to synthesise a typical Eastern Cordillera situation in Colombia, South America. The structures and velocities used were taken from Alfonso (2001) and the ANH website (see References). In the full elastic model the shear-wave velocities were taken from various formulae for the lithologic units in the model (Castagna et al, 1985; Christensen et al, 2003).
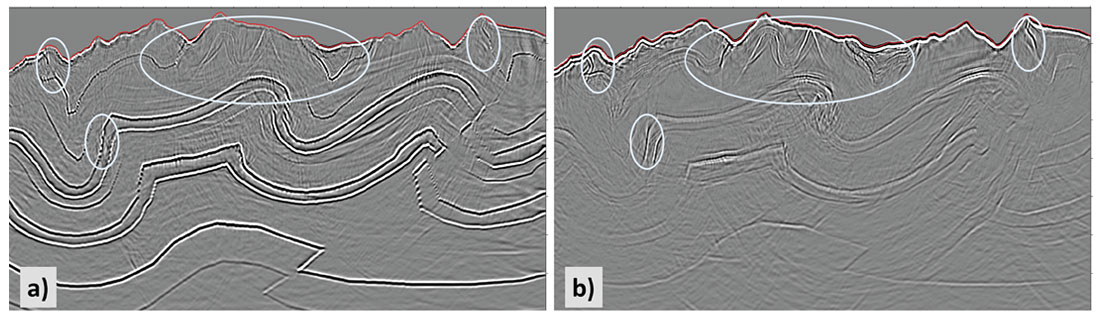
Elastic-wave data were also generated from this model using two different acquisition scenarios. The first model used acquisition parameters typical of recent cable-based seismic surveys in the Alberta Foothills, with a receiver interval (RI) of 60m, a source interval (SI) of 120m and a maximum offset of 5 km. The second model uses acquisition parameters that could be achieved using a node-based system with a RI of 15m, a SI of 60m and a maximum offset of 15 km. Despite the fact that two parameter sets are changed between these models it is quite easy to observe the effect of each parameter- set change independently. Some of the deeper dipping events are imaged with a 15 km offset (Figure 5a), but are not imaged with a 5km offset (Figure 5b). The finer spatial sampling (RI=15m /SI=60m), shown in Figure 5c, shows minimal aliasing artefacts in the shallow events whereas the coarser spatial sampling (RI=60m /SI=120m), shown in Figure 5d, shows considerable spatial aliasing in the shallow image.

One reason for generating this model was the observation by Alfonso (2001) that poor imaging in part of the section might be due to high velocity at the surface. To test the hypothesis that this might be partly due to high emergent angles at the receiver, the vertical and radial component were again imaged using elastic-wave RTM with the P-wave velocity field. It may be seen in Figures 6a and 6b that there is indeed substantial PP energy on the radial component.
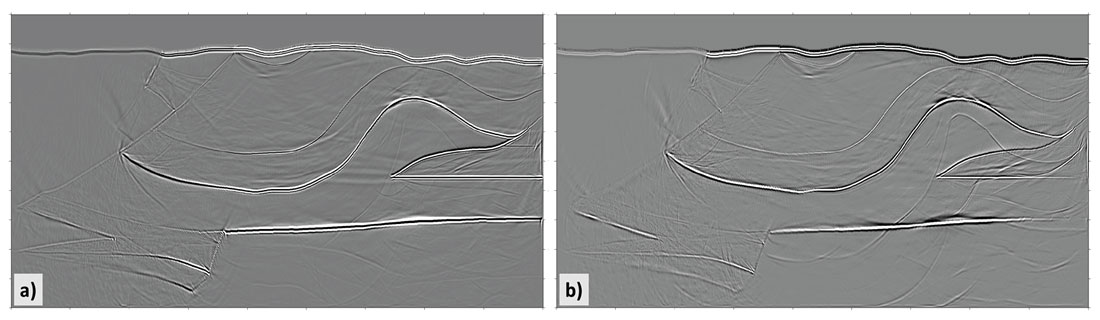
(a) Vertical component, 15 km aperture, P-wave velocity function
(b) Radial component, 15 km aperture, P-wave velocity function (PP signal on Radial)
Conclusions
The potential benefits of using node-based acquisition systems in terms of improving seismic imaging have been demonstrated. These benefits include the potential for improved spatial sampling through reduced receiver intervals, improved shallow imaging through reduced receiver line intervals and improved steep-dip imaging through the acquisition of longer offsets. These imaging benefits may also come with improvements in safety, ease of operations and potential cost savings by removing the need for cables and the requirement to place receivers in undesirable or unsafe locations. With more freedom in siting receivers it becomes possible to design 3D surveys combining jittered sampling with surface imaging tools such as LiDAR and satellite digital elevation models for the best locations and to test these for their performance in sparsity promotion imaging techniques that follow from compressive sensing concepts.
Furthermore the use of 3C sensors is readily enabled through the use of node-based acquisition systems with the potential to avoid some of the problems encountered in rough topography in hard rock areas and with the long offsets required to detect the reflected signal from steeply dipping layers. Poor image areas on rugged topography frequently correlate with fast near surface conditions and imaging all three components through elastic RTM, for example, would enable imaging of the severely attenuated P-wave energy obtained from the purely vertical component of a 1C sensor.

Acknowledgements
We acknowledge Hector Alfonso (Ecopetrol), Saul Guevara (Ph.D. student), Sam Gray (CGG) and Rob Vestrum (TBI) for general discussions, Judith Chan, Lorenzo Casasanta and Adel Khalil (CGG) for building, imaging, cleaning and enhancing the model data images, and CGG management for allowing the publication of this paper.










Join the Conversation
Interested in starting, or contributing to a conversation about an article or issue of the RECORDER? Join our CSEG LinkedIn Group.
Share This Article