The subtle effect of attenuation

When you wake up in the morning, you look at yourself in the mirror – at least I hope you do! You are able to see yourself because light rays are reflected when they hit the opaque but shiny back surface of the mirror. Later, when you are on a bus or train, you see yourself reflected in the window, but not as sharply as in the mirror. That is because only a small percentage of light rays reflect back; most of them transmit through the glass. That is why others outside the bus can see you.

The same principles apply to the seismic waves in the earth. The following famous equation for reflection coefficient R shows how much of the wave amplitude is reflected from a normally incident seismic ray when it hits a boundary:

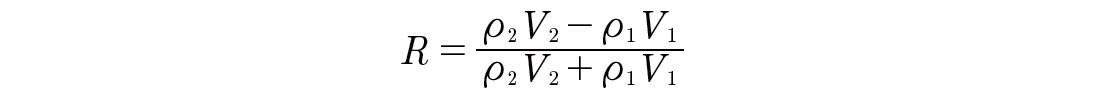
where ρ and V are density and P-wave velocity, respectively. The subscripts represent the layers across the boundary, with 1 being the upper layer. The product of the velocity and density is called the acoustic impedance. The equation shows that when there is an acoustic impedance contrast between the two layers, there will be reflection. But this equation is actually an approximation. Research shows that there is another contrast that contributes to the reflection of the waves and rays in exploration seismology, and that is attenuation contrast

Attenuation is the loss of energy in the form of heat. Particles oscillate in their place without flowing from one location to another, to allow the seismic waves to go through. These particles turn some of the seismic wave energy into heat due to friction forces. You can think of this energy loss as a sort of currency exchange fee. Every time you exchange one currency for another, the bank charges a transaction fee, which is deducted from your money. If you do the exchange several times, you lose more and more of your money. As an experiment, start with some of your local currency and exchange it to a few foreign currencies in turn and then convert it back to your local money. You will see that a signi!cant portion of the money is gone! This loss, in seismic terms, is called attenuation and is measured through a parameter called quality factor Q. In fact Q is inversely proportional to the attenuation.

When we account for attenuation as well as acoustic impedance, Lines et al. (2008) showed that we can write a more accurate version of the reflection coefficient equation:

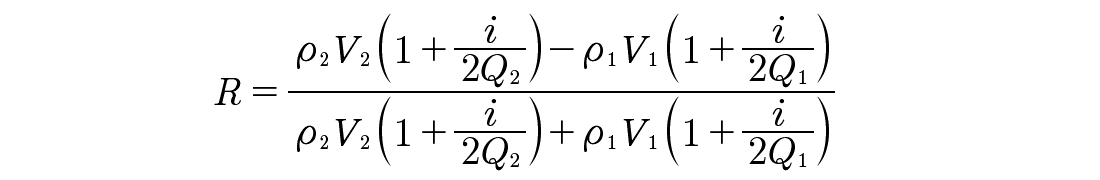
It results in a complex reflection coefficient. This equation reduces to the simpler form when there is no contrast in the quality factors, i.e. when Q₁ = Q₂.

Imagine a two layer model with the following properties: ρ1 = ρ2, V₁ = 2000 m/s, V₂ = 3500 m/s, Q₁ = 40, and Q₂ = 6.28. The reflection coefficient R calculated using the simple equation opposite is 0.273, which means the amplitude of the reflected wave is 0.273 times the amplitude of the incident wave. The result including the attenuation effect is the complex number (0.274 + 0.031i), which means the reflected amplitude is 0.276 times that of the incident wave (0.276 is the modulus or magnitude of the complex reflection coefficient), and the phase rotation between the incident and reflected waves is 6.4° (the argument or phase angle of the complex number).

Since the difference between the predicted amplitudes and phases of the reflected waves calculated from two equations is small (in real cases, seismic noise makes the relative effect even smaller), it is within reason to say that the familiar equation is a good approximation of the reflection coefficient for most scenarios. But Q is in there somewhere!

References

Lines, L, F Vasheghani, and S Treitel (2008). Reflections on Q. CSEG RECORDER 33, 36–38.

Q&A:

Your Ph.D. research work focused on attenuation behavior of heavy oil or oil sands. Tell us about it.

It all started with the SEG workshop on heavy oils in the summer of 2008. At the end of the workshop, one of the main conclusions was that geoscientists needed to focus more on the viscosity of the heavy oils rather than just density. After returning to Calgary, Dr. Lines, my supervisor, and I decided to pursue this target. Coming from an engineering background, I knew that in fluid mechanics, the shear properties of the fluids are important. This was contrary to what geophysicists in the conventional exploration world always assumed, that fluids do not support shear and the shear velocity and modulus of fluids are zero. One day, I found a table of measured shear wave velocities of different material. In that table, the shear wave velocity of honey was measured at room temperature to be around 13 m/s. It was not fast enough, but was not zero either. This sparked the idea that there must be a way to characterize the shear properties of the very viscous fluids.

With support from CHORUS and Dr. Lines, I was able to work on this idea and come to the conclusion that variations in the viscosity of heavy oils are reflected in the attenuation parameters of the seismic signal. If recorded and estimated accurately, Q which is inversely proportional to the attenuation coefficient can be used to estimate viscosity of heavy oils.

I have been in the industry for close to 30 years. In my early days I learned about attenuation, and its quantification in terms of the quality factor, Q. How much more do we know about attenuation now, than say 30 years ago?

In theory, what we know about attenuation today is not that different from what was known a couple of decades ago. In fact the topic of attenuation is very well theorized. Something that we can do better now than before is to record data with higher frequencies. The effect of attenuation is more pronounced when we have higher frequencies in the signal. Also we have learned during the past couple of decades that attenuation is really hard to get, especially when working with surface seismic data. We also know that contrast in Q causes reflection.

Would you say we can accurately apply attenuation correction to seismic data today? If not what prevents us from doing so?

This is a tricky question. If we knew the attenuation coefficient, yes we could accurately apply the correction because the attenuation mechanism is relatively well understood and fast processing algorithms are readily available. The problem is that attenuation parameters are very delicate. The workflows that we currently use to estimate attenuation coefficient from seismic data are very sensitive, and most often we do not have the right data with high enough frequency content to extract attenuation parameters from, namely cross borehole or VSP data. It is important to mention that in the oil and gas exploration scales, the attenuation coefficient of solids and low viscosity fluids are so small that the change in the signal is not detectable at all. It is when seismic waves travel through specific material such as very high viscosity fluids with high attenuation coefficients that the effect of absorption becomes detectable.

If attenuation correction is not applied accurately to the seismic data, or not applied at all, what are we missing in our interpretation of that data?

Attenuation works on the traveling waves all the time. It changes the signal amplitude and phase spectra and causes non stationarity. If you have time and the right data to work with, then accurate correction for attenuation effects is really nice to have, if not, I don’t think the exploration seismology would turn upside down. However, similar to other attributes, attenuation coefficient can provide vital information that is hard to explain with other attributes. For example, while I was generating the cross borehole Q tomograms for my thesis I noticed that the shales at the top of the bitumen layer, which act as the cap rock, are brightly illuminated, while they were not obvious on the velocity tomograms. This is because the water saturated shales in this case do not have acoustic impedance values much different from the bitumen saturated sand, but because of the difference in fluid viscosity, shales exhibit very different attenuation characteristics than sands, and this is reflected in their different Q values.

I think that the Pareto Principle, which is also known as 80/20 rule, applies to this case as well. Pareto principle says that 80% of the effects come from 20% of the causes. In other words, you could get 80% accuracy in your solution by only spending 20% of your time and money. If you think that what you are looking for rests in the subtle effects of Q, then you can spend more resources on the data to extract and apply the attenuation effect.

Are you aware of anyone using your method for characterizing heavy oil formations?

I know that the methodology I introduced in my thesis has been used in at least one study in the industry in which the objective was to estimate the mobility of the heavy oils in the reservoir. Mobility is defined as the ratio of permeability over viscosity. As discussed in my thesis and shown in other publications on poroviscoelastic theory, attenuation varies not only with viscosity, but also with permeability as well as other reservoir parameters, and therefore can be applied in a wide variety of reservoir characterization projects.

Could you tell us the directions in which the research efforts are being made to determine attenuation and characterize reservoir with it?

There are great researchers at Universities of Calgary, Saskatchewan and Houston, and Colorado School of Mines who work on the effects of Q. A few years ago, Dr. Lines et al. published a work titled reflections on Q, where they explained that contrast in attenuation contributes to the reflection coefficient of a boundary. In other words, if materials across a boundary have no contrast in acoustic impedance, you can still observe reflections from that boundary if there is a contrast in attenuation. Such reflections also show a small phase rotation. Scientists at CREWES have established a physical model and made a few experiments to confirm these reflected energies using two different substances with similar acoustic impedance values and different attenuation coefficients. Of course it is not as simple as it sounds. There are several issues that need to be carefully resolved to obtain valid results. For example Q is frequency dependent, and lab tests are normally carried out with very high frequency sources, on a model of much smaller scale. Extrapolating the results to the reservoir scale is not just a simple task and requires careful upscaling of attenuation effects. The Centre for Rock Abuse at Colorado School of Mines and Rock Physics Laboratory at University of Houston have conducted measurements of the heavy oil shear properties such as shear wave velocity and attenuation. Theoretical research is also being done at the University of Saskatchewan. All of these suggest that the assumption that fluids do not support shear might not be a good assumption, at least when we are dealing with heavy oils.

In what other fields the attenuation effect is important?

Everywhere we deal with waves of some sort, we are dealing with attenuation, for example in astronomy or wireless telecommunication. Almost every astronomical discovery relies on the recorded electromagnetic signal. Age, distance, composition, or displacement of interstellar objects are all determined from the spectrum of the signal radiated by that object. Higher frequencies attenuate faster and more severely. This means that objects appear redder than they are because the blue light waves with higher frequencies are attenuated more. Of course other mechanisms are involved in the interstellar reddening such as scattering. Such effects should be removed before any conclusion is made. It is important to mention that attenuation should not be mistaken with power loss in signals due to geometrical spreading. These are two different mechanisms and should be considered independently of each other.

As someone has said ‘every new idea looks crazy at first’. According to you, what are a couple of ‘crazy ideas’ that have the potential to pan out well?

I think DAS technology, diffraction imaging and reconstruction of irregularly sampled seismic data could be the new realities of exploration seismology. Once these techniques are mature enough, it is possible to spend less and get more from seismic data. The DAS technology has a few glitches that once sorted out can be used in a vast number of possibilities that were unimaginable not long ago such as pipeline monitoring, continuous 4D reservoir monitoring and even border control! Diffraction imaging is also very interesting. In a conventional signal processing flow, every effort is made to remove the diffractions from the data because they are regarded as unwanted energy in the specular reflection domain. However, it is nice to remember that Huygens principle states that every point on a boundary act as a diffraction point and it is the sum of all these diffractions that forms the reflection event on the seismic section. So, in short, diffraction is our friend. It is only at the edges and corners that the summation does not add up to a nice reflection, and the image is left with diffraction hyperbola. If these remaining hyperbolae are imaged rather than removed, they can provide a sharp image of the edges and discontinuities such as faults. I am not familiar enough with the irregular sampling theory but the promise is that you can go beyond Nyquist frequency and wavenumber, and also can use the exact location of the geophones rather than assuming the grid is perfectly uniform. Non-uniform layouts can also help optimise the survey which means better and cheaper data.

What is the most important thing that you learnt or which has influenced you in your life?

Oh! This is a tough one. I think the most important thing that I have learnt through observation is that people who focus on the positives and see the glass half full are in my opinion generally happier and more successful. I also believe that today should be a better day than yesterday. It does not have to be better by a lot, as long as the slope is positive, I consider it a good day. I also would like to repeat this quote from Louis Pasteur that “chance favours the prepared mind”.