Value of Integrated Geophysics

Introduction

In the second VIG column (Wikel, 2013), Kurtis Wikel gave an excellent overview of the history and early identity crisis of geomechanics as a specific discipline in the oil and gas industry. He also discussed the challenges associated with moving geomechanics from traditionally wellbore-based analyses to a full 3-D understanding through integration with geophysics and microseismic. It was an excellent article, concluding with the hope that “the interaction between engineers and geophysicists will hopefully become more of a two-way street.” Wait a second, what happened to the geomechanics? Admittedly, the term geomechanics still gets used far more widely than perhaps it should, but completions engineering (used here to include hydraulic fracturing), is not geomechanics. This article is our plea to get engineers, geophysicists AND geomechanics specialists speaking the same language and working together. Rather than a two-way street, perhaps what we need is something along the lines of a roundabout.

Where Are We Now?

Geophysicists and geomechanics specialists have to agree that most of the questions we are being asked to answer these days are being driven by engineering. Whether or not it is true (which we’ll discuss a bit later), the current thinking is quite frequently that if you get the completion and stimulation right, you’ll have a producer. What does “right” mean, exactly? Wouldn’t we all be rich if we knew the answer to that question!

The engineering side of things in turn is governed by operational decision-making – Open-hole or cased? How many stages? What should the stage spacing be? How much proppant should we pump? What kind of proppant should we use? What’s our breakdown pressure going to be? The answers to those questions, however, are geological and translate into questions like what are the rock properties and stresses where I’m going to put this well? Traditional geomechanics can answer those questions rigorously, but only where there’s already well data. Geophysics can answer them where there isn’t well data, but only in a relative sense.

We, the authors of this paper – one a geomechanics specialist and the other a geophysicist – work for a small service company in downtown Calgary. Our paths cross several times every day, and we look at a lot of the same things in our work such as stress and rock properties, etc., yet we do not work together. It’s certainly not for a lack of wanting to; we know full well that we should be. It is simply a reflection of the division that exists in our client’s offices as well.

Why the separation?

The authors asked each other the following question – what are my discipline’s views regarding the other discipline? We thus learned that geophysicists think geomechanics people are too focused on well data, keep complaining that geophysicists are doing things wrong but aren’t helping them do things differently, are not solving the problem of prediction, and are too few and far between. Conversely, geomechanics specialists think geophysicists are not focused enough on well data, won’t listen to geomechanics specialists when they try to tell them how to do geomechanics right, think they have all the answers, and exist in numbers too large to be influenced. We also came to realize that although we are often talking about the same things, we use different languages. For instance, we both talk about rock mechanical properties such as Poisson’s ratio and Young’s modulus, but the geomechanics specialist is talking about static values or dynamic values measured in core or logs at ultrasonic or sonic frequencies, whereas the geophysicist is talking about dynamic values measured at seismic frequencies.

Another source of friction comes from what geomechanics specialists perceive as other disciplines trying to “do geomechanics” without fully understanding the applicability and the limitations of the methods they are applying. You are unlikely to find a geomechanics specialist trying to do seismic inversion or calculate proppant placement, but you will frequently find a hydraulic fracture modeler calculating stress from logs and a geophysicist calculating brittleness, for example, from seismic.

The Value in Integration

If you think about it, the three disciplines – engineering, geophysics and geomechanics – are really quite complementary. Engineering dictates what the important parameters are, geophysics can provide predictions of those parameters between wells, and geomechanics can provide calibration points, or “ground truth,” for the seismic-based predictions. Let’s use natural fractures as an example. In the first VIG column (Hunt, 2013), Lee Hunt used fracture density to illustrate the concept of a V-argument in which several factors contribute to an argument which is not wholly dependent on any one of them. In this example, the four contributing factors were all parameters that are derived from seismic to assess the expected fracture density in a potential well.

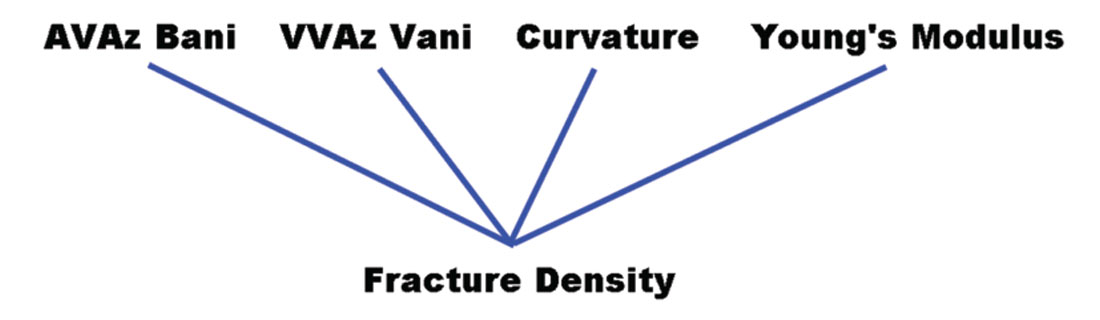
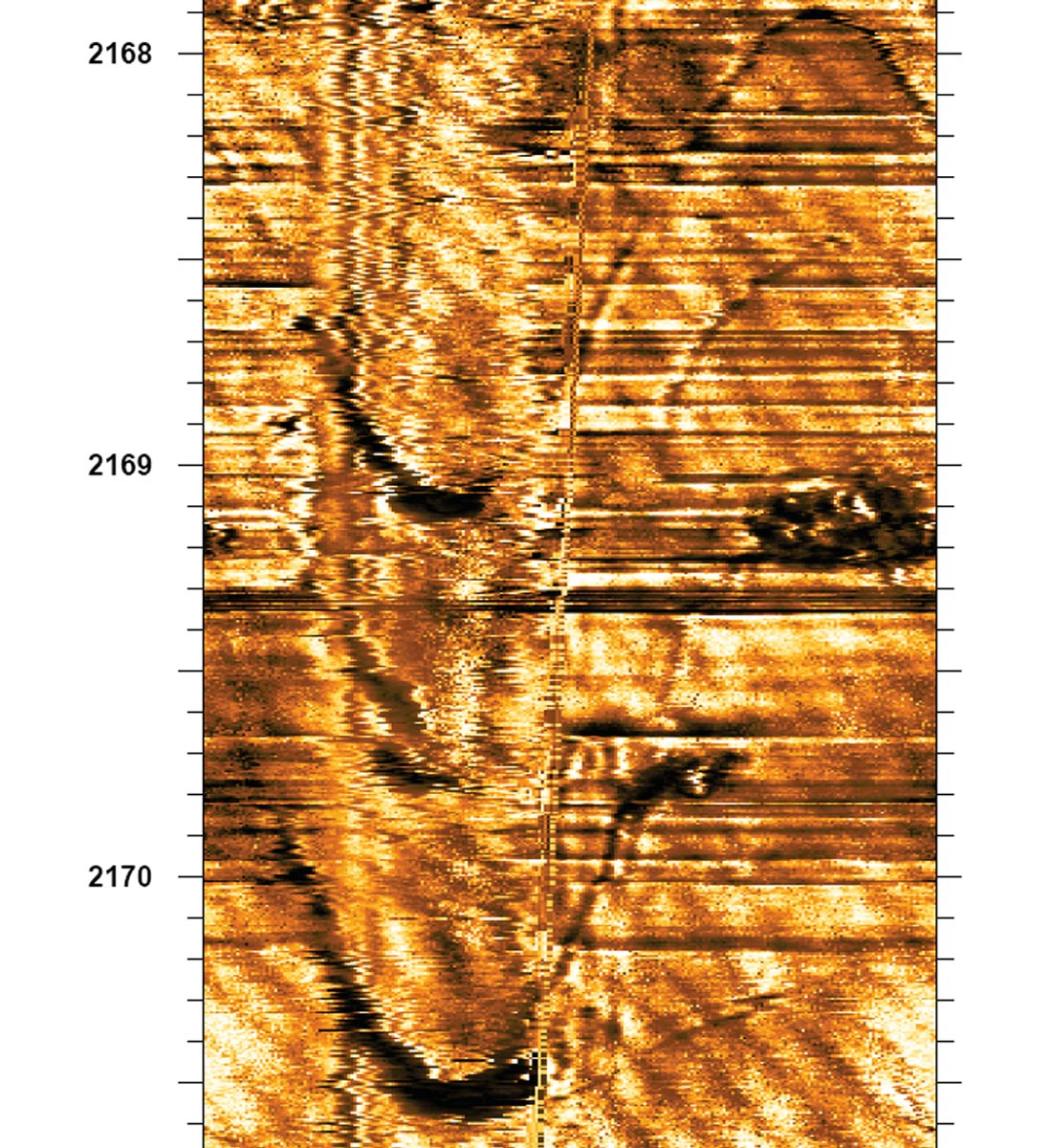
We know from fracture mechanics that fractures and their characteristics – orientation, density, permeability, frictional strength, etc. – are a complex function of structural position (e.g., fold curvature, proximity to faults), rock properties (e.g., strength, layering, fluid content and pressures), and stress history (e.g., multiple episodes of burial, deformation, uplift, unloading, etc.). The only way to truly understand a fracture population is to measure it in situ, at depth, which we can actually do using wellbore image logs (Figure 2). Only then can we determine how accurate our predicted fracture population was. If we did this more often, would it alter how we make our predictions?

With this in mind, let’s look at a few more popular geomechanical properties that have made their way into the geophysical domain some of which are already identified by Wikel (2011).

Elastic Parameters

Elastic moduli are used in constitutive equations to describe how elastic materials deform by quantifying a given strain in response to an applied stress. For example, in a linear elastic material, strain is linearly related to stress and is totally recoverable once the stress is no longer applied. The constitutive equation for linear elasticity can be expressed as:

where S is stress, ε is strain, λ is the Lamé constant (or Lamé parameter, singular; a.k.a incompressibility in the seismic world), and G is called the shear modulus (modulus of rigidity, or just rigidity; a.k.a S or μ in the seismic world). Other important elastic moduli include Young’s modulus (or modulus of elasticity, also referred to as stiffness, usually denoted as E), which is the ratio of applied stress to resulting strain in the same direction, and Poisson’s ratio (usually ν), which is the ratio of lateral expansion to axial strain. Elastic moduli are all related to each other, and thus the constitutive equations can be constructed using various combinations of them. There are many other constitutive laws that account for such things as time-dependence (viscoelasticity), pore fluids (poroelasticity), temperature-dependence (thermo-elasticity), material damage (plasticity) and various combinations of these. The key is to remember the basic concept and, when working with stress and strain, make sure to use the right equations with the right parameters for the application.

At this point the reader may have noticed a certain lack of consistency in symbols and terminology. For instance, above we mentioned that S is sometimes used to denote the shear modulus, but we also use S for stress (usually with subscripts denoting directionality or relative magnitude). μ is also commonly used for the coefficient of friction (sliding or internal). Unfortunately, nomenclature and notation tends to be unique to individual fields like geomechanics and seismic, which of course makes communication between them even more difficult!

In geophysics, AVO inversion of seismic data is regularly used to measure the P-impedance, S-impedance, and density of the subsurface. These attributes are then converted into other elastic properties such as Young’s modulus, Poisson’s ratio, and the “Lamé parameters” λρ and μρ. There is a large and increasing body of work showing the utility of these measurements and their ability to identify variations in fluids and lithology. This is the point at which geomechanics would like to point out that these properties may not only vary with rock type, but also with measurement method, the scale at which they are measured and even the direction in which they are measured.

From a geomechanics standpoint, rock moduli have both static and dynamic values. Deformational tests give us the static moduli (Figure 3), whereas dynamic moduli are calculated from sonic wave velocity (logs, seismic, and ultrasonic lab tests) and rock density. The static, sonic (log-based), seismic and ultrasonic dynamic values may be significantly different (Figure 4), so it is important to specify which one is being reported and to know which one to use for various applications. Static Young’s modulus, for example, is usually 70-80% of dynamic Young’s modulus, and to further complicate things the ratio of static to dynamic Young’s modulus is stress-dependent.

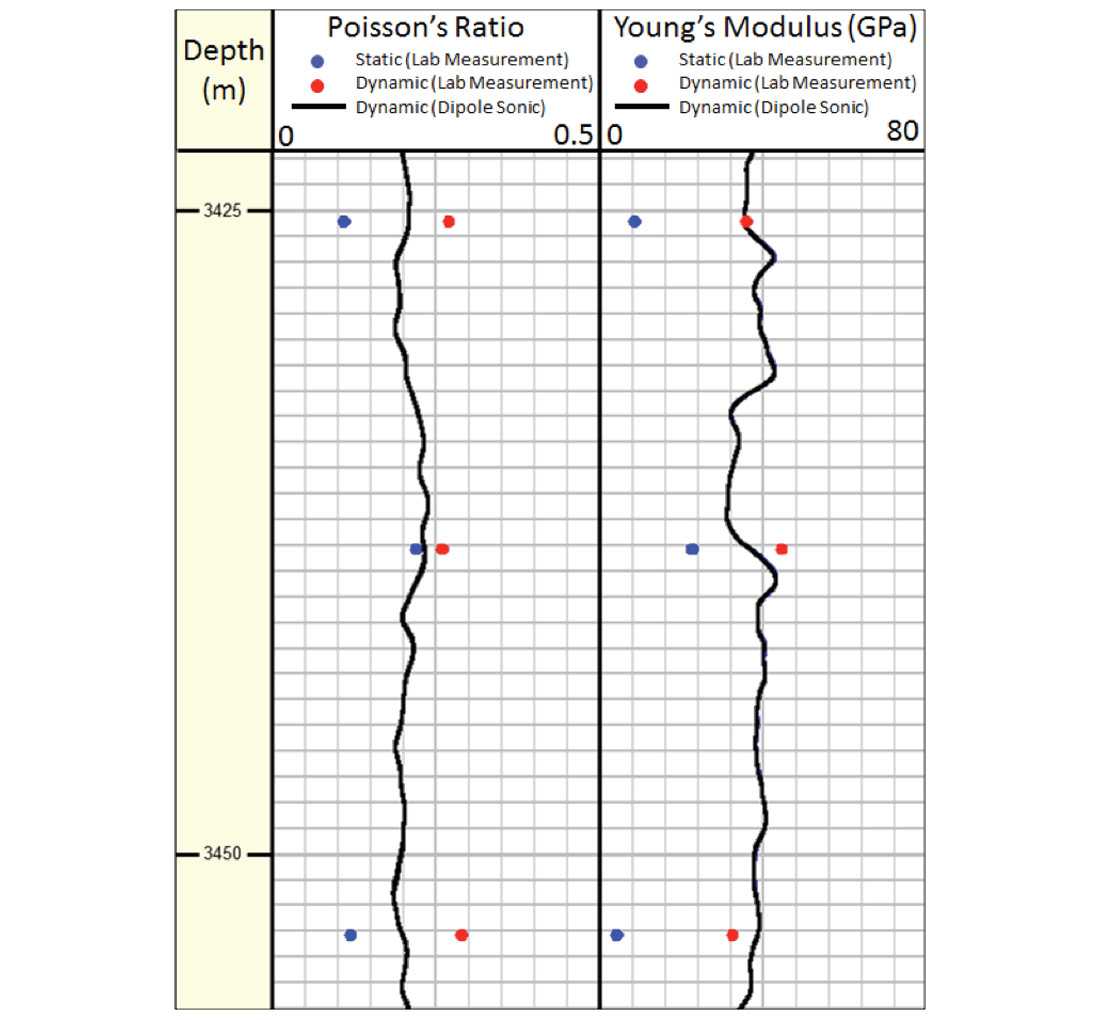
Considering all of this, it is clear that robust (not necessarily extensive) rock testing programs should be designed, with a full geomechanical understanding of the limitations and applicability of the results. These tests can then be used to validate and/or calibrate a seismically derived elastic parameters through establishing relationships between static and dynamic parameters for specific zones of interest. Only by applying this workflow repeatedly will we then begin to understand under what conditions we may be able to rely on seismic values without needing verification.

Brittleness

Presently, one of the more popular attributes being calculated, either from logs or seismic, for shale plays is the brittleness index, commonly defined as:

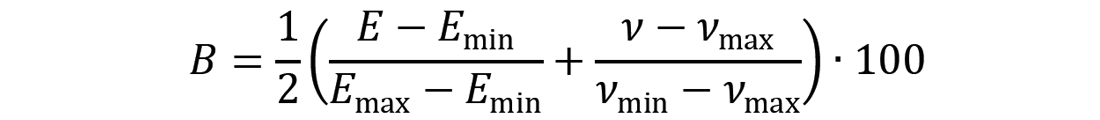
It is a weighted average of Young’s modulus (E) and Poisson’s ratio (ν) attempting to describe a rock’s ability to fail under stress and maintain a fracture (Rickman et al., 2008). Here the minimum and maximum values of these elastic parameters pertain to the formation being analyzed.

The attractiveness of this attribute is that it seemingly describes the ability of a shale to be hydraulically fractured knowing two readily available attributes. With a dipole sonic log measurement, or an AVO inversion of seismic data, Poisson’s ratio and Young’s modulus are easily calculated. The drawback of this method is that it is purely empirical, and without establishing its correlation with rock failure, there may be no link between the two.

In geomechanics, rocks that are both stiff and weak are said to be brittle. Stiff implies minimal deformation prior to failure under applied stress, and weak means that the rock fails at a relatively low stress. As mentioned previously, Poisson’s ratio and Young’s modulus describe deformation, not failure. Nowhere in the definition of brittleness given above is there a term that includes rock strength. Originally, rock brittleness was defined mineralogically with rocks having a higher quartz content being more brittle. Indeed, in a review of multiple shale plays, Britt and Schoeffler found that some of the characteristics of prospective plays are that static Young’s modulus is greater than 3.5 x 106 psi (24.1 GPa) and they contain less than 40% clay content.

The utility of the seismic brittleness index in shale plays other than the first to which it was applied is not yet understood. By adjusting the formulation of it to include something reflective of the rock strength and/or the rock composition, we may find that it works better and can be used more widely.

Stress

Stress may be determined from seismic data (e.g., Gray et al., 2012). The overburden density required for vertical stress estimation may be obtained from AVO inversion, provided sufficient incidence angles are acquired. The two horizontal stresses are then calculated as a function of the vertical stress, along with Young’s modulus, Poisson’s ratio, and a term describing the azimuthal anisotropy of the rock. The term “closure stress” in geophysics is used to refer to the minimum horizontal stress.

Similar to the seismic workflow, log-based calculations of stress also calculate horizontal stresses from vertical stress as determined from density logs. Either way, this approach to stress determination uses what is referred to as the bilateral constraint (or uniaxial strain condition/assumption), in which all horizontal stress is derived from the vertical stress and rock deformation described by elastic moduli. The correction applied to describe a difference between the horizontal stresses is really an arbitrary attempt to account for a tectonic component in one of the horizontal stresses.

In geomechanics a good understanding of all three principal stresses is the most important component in the characterization of a formation. Integration of a density log or density data from seismic is a perfectly acceptable way to obtain the vertical stress, and usually (but not always) the vertical stress is one of the principal stresses. Numerous types of downhole measurements can be performed to determine least principal stress, which may be either the vertical stress (normal faulting environment) or the minimum horizontal stress (strike-slip or reverse faulting environment). The only accurate way to determine maximum horizontal stress, however, is from the mechanical interaction between the wellbore and the in-situ stress conditions, which must be modeled (Zoback, 2010).

Stress is of course critical in hydraulic fracturing. Firstly, when fracturing, the induced tensile (mode I) fracture will open in a direction parallel to the minimum principal stress. When pumping is stopped and the pressure in the induced fracture drops below the magnitude of the minimum stress, it closes. Thus the real closure stress is essentially equal to the minimum principal stress if you considerable the tensile strength of the rock to be negligible. In a normal faulting environment, minimum stress is vertical, hydraulic fractures are horizontal, and the assumption that closure stress is horizontal is incorrect. Secondly, when the hydraulic fracture is initiated and until it propagates roughly two borehole radii from the well, it is controlled by the wellbore stress concentration, which is a complex function of the well and stress orientations and can be very significantly different from the far-field, natural stress condition. Finally, scale is an issue. The variation in horizontal stresses predicted by logs and used in hydraulic fracture modeling is much finer than can either be inferred from seismic or determined from wellbore modeling. This, of course, complicates any potential workflow that would use wellbore modeling to calibrate the engineering results. One workaround may be to use log-based calculations as a relative measure, not an absolute measure of stress.

Conclusions

As we have hopefully illustrated in this article, much of the frustration in geomechanics circles seems to be from a perception that geophysics is oversimplifying some very complex geomechanical topics and delivering important data to engineering that’s been determined in a non-rigorous way. But geophysics is far too valuable a tool for geomechanics to backseat drive – that is, to simply proclaim that geophysicists are doing everything wrong. We believe that by applying geomechanics fundamentals to geophysics, even more value could be added. Tests on rock samples should be conducted, and results shown in support of established relationships that are able to use seismic-derived properties. Not only would geophysical analyses be more reliable, but geomechanics would gain an important new tool for determining geomechanical parameters.

Acknowledgements

The authors would like to thank Mehrdad Soltanzadeh for Figure 4 and review of this manuscript.