It is a common misconception that the artistic depiction of people is forbidden by Islam. Scholars debate this – various hadiths contain such prohibitions, but many of them are specific to this or that sect within Islam. But regardless, within the Islamic world the depiction of people in art, especially the prophet Muhammad himself, has been avoided for fear of backsliding into idolatry, the worship of objects. The result of this deep rooted historical aversion is that visual artistic expression within the greater Islamic world blossomed in two abstract areas: calligraphy, and the topic of this article, geometric mosaics.
Mosaic, the art of creating an image using a palette of different coloured small pieces of some material, is ancient. Some of the earliest examples, in Mesopotamia for instance, used pebbles, or fragments of sea shells. Over the centuries the art gradually evolved and became more sophisticated. A big step forward came with the development of coloured glass and ceramic – the fragments or shards of these materials were an obvious choice for mosaics. The ancient Greeks were the first real masters of mosaic art, and Greek artisans were in demand throughout the Mediterranean region well into Roman times. During this era mosaics tended to be made with ceramic tile fragments and featured prominently in floors, such as those seen at Pompeii. Hundreds of years later the Byzantine (medieval) Greeks created mosaic masterpieces on ceilings and walls, using smaller pieces, more glass and exotic reflective materials. Figure 1 is from the Hagia Sophia in Istanbul (formerly Constantinople), and features the Emperor John II Comnenus and his wife Irene flanking the Madonna and baby Jesus; it dates from 1118 AD.

As the Byzantines were gradually encroached upon and eclipsed by the Arabs and Turks from the south and east respectively, it was a time of fertile cultural exchange. Figure 2 captures this dynamic perfectly. It is an image of what is known as the Aleppo Room, on display in Berlin’s Pergamon Museum. Commissioned by a wealthy Christian in Aleppo in ~1601-1603 AD, it features the finest Ottoman craftsmanship of the time, and incorporates Arabic, Christian, Persian and Ottoman elements and motifs.

The Islamic Ottoman Empire eventually gobbled up the Christian Byzantine, including its art and architecture, and as it rose in power and scope, it spread the use of mosaics throughout a broad geographic sphere of influence, leaving a rich legacy of mosaic treasures in a vast east-west Eurasian arc. As anyone who travels knows, there are stunning mosaics found throughout the regions influenced by Islamic culture, from the Alhambra in Spain, through Egypt, Turkey, and all the way around to places in Central Asia such as Tashkent and Samarkand (Figures 3, 4, 5). It turns out that the mosaic shown in figure 4 is contemporary, dating from around 1935. Upon closer inspection my colleague Mehran Gharibi (whose photo it is) and I noticed that the star has 17 points, meaning it has a symmetry of one and 17 – very unusual, but more on that later. It is interesting to note that the evolution and use of geometric mosaics continues to the present in the region.


I had long admired the beautiful intricacy of Islamic mosaics, but not for one second ever pondered how they were designed. In 2009 I read a fascinating article in Saudi Aramco World (Prange, 2009) which inspired this one. Subsequent to that, my friend Matteo Niccoli gave me links to several scholarly math papers on the topic, none of which were as inspiring or easy to read as the first, but fascinating nonetheless, and which further illuminated the topic. My research related to the writing of this article uncovered even more articles, and it’s obviously a topic that interests scientists.

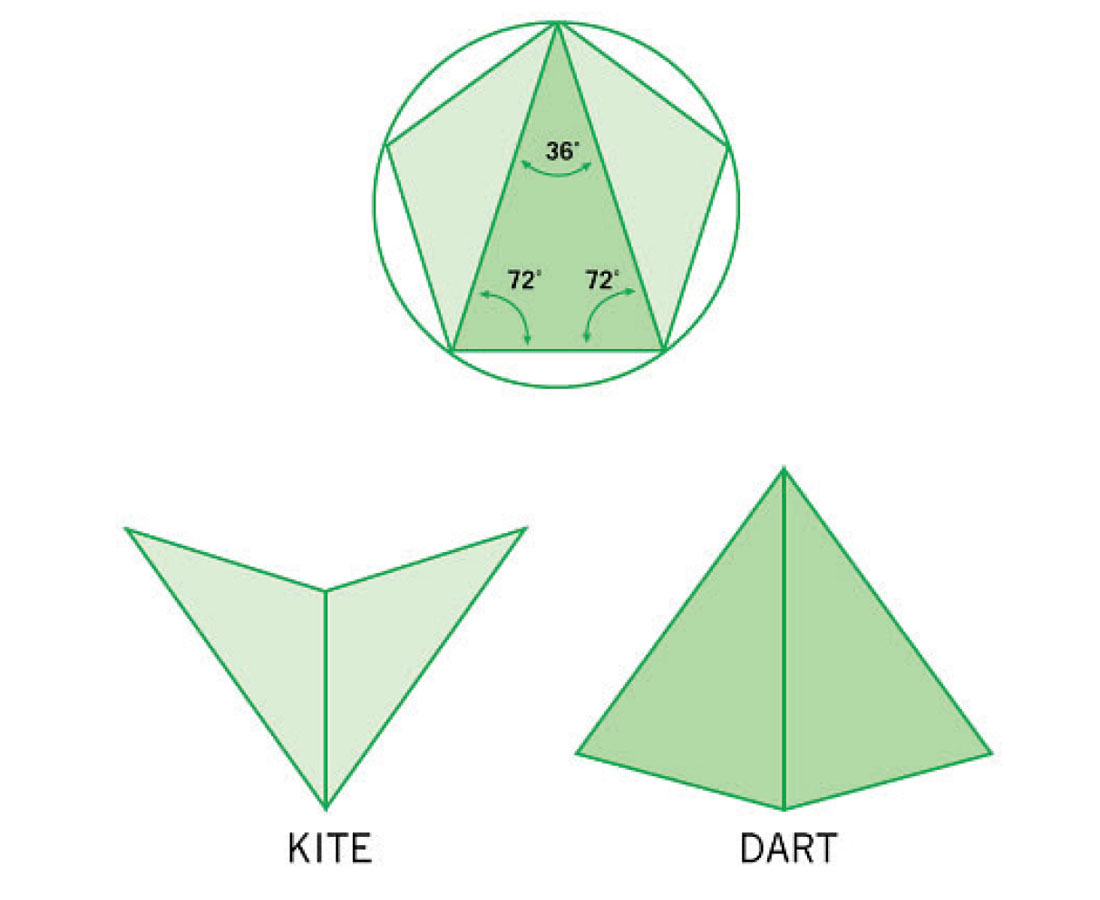
In his article Prange (2009) describes how a physics graduate student, Peter J. Lu, on a visit to Uzbekistan, was intrigued by the mathematical design principles underlying the mosaics he saw there. This led to his identification of five basic underlying shapes found in many of the mosaics, which he coined ‘girih tiles’ (Fig. 6). Eventually, studying what is considered perhaps one of the pinnacles of the art, the Darb-e Imam (literally, portal to the shrine of the Imam) in Isfahan, Iran, he had a eureka moment – he connected the girih shapes to Penrose patterns (Fig. 7). These latter two basic shapes, darts and kites, were defined by the British mathematician Sir Roger Penrose in 1974, as forming the foundation for a set of entirely non-repeating patterns, which is what some of the Islamic mosaics are. Penrose’s paper in 1974 was a breakthrough of sorts, as in this obscure (aren’t they all?) corner of mathematics, people had for decades been unsuccessfully investigating whether there were indeed shapes which when combined would produce only non-repetitive patterns, as opposed to shapes which produce only repetitive patterns (e.g. hexagons) or ones that produce a mix of repetitive and non-repetitive, both of which are a dime a dozen. In Penrose’s scheme, there is only one rule: no two adjacent tiles can form a parallelogram. What happens as patterns are created with his tiles and get larger and larger is that the ratio between kites and darts approaches the “golden ratio” of 1.618. It can easily be shown that the girih tiles can be created using only the Penrose shapes. If a medieval mosaic designer created a pattern in which no two component darts or kites side by side formed a parallelogram, then – voila! – an infinite, non-repeating pattern would have been born.
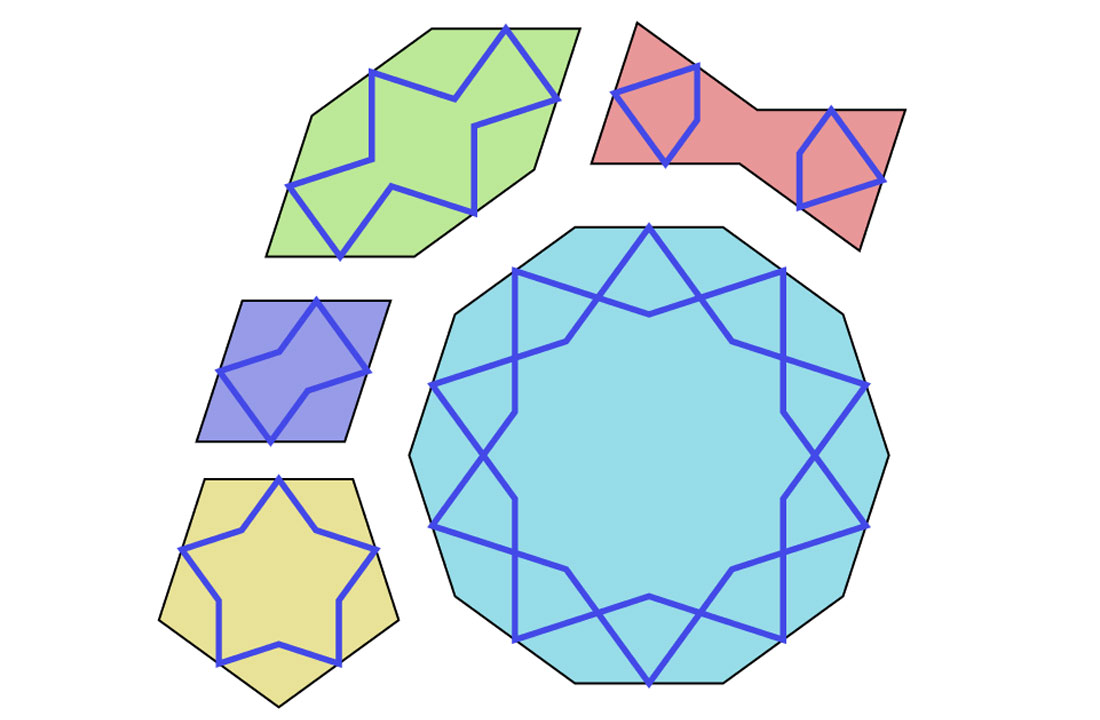
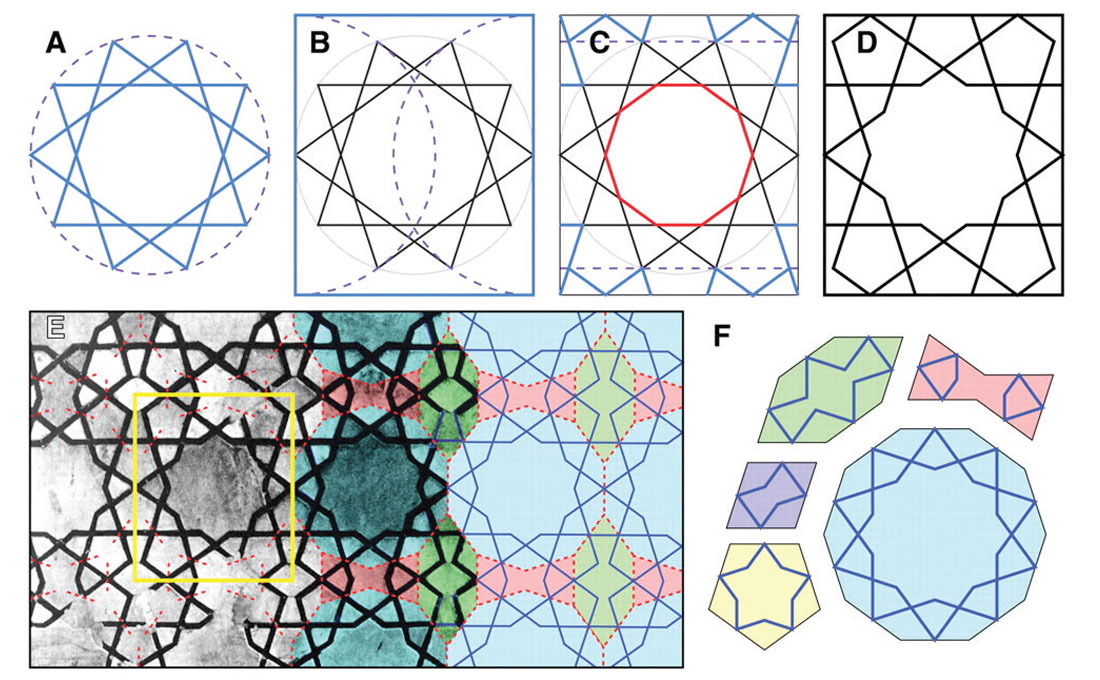
Conventional belief has been that the patterns seen in Islamic mosaics were based on simple geometrical principles and created using simple straight edge and compass tools, especially the straplines – continuous decorative lines made up of straight segments – which are a characteristic feature of these mosaics. Figure 8 shows a section of the Darb-e Imam spandrel which contains very prominent straplines. In his article Prange (2009) incorrectly states that girih is the Farsi word for knot, confusing it with gereh. In fact, Lu’s use of the word girih is apt, as it refers to, “an Islamic decorative art form used in architecture and handicrafts (book covers, tapestry, small metal objects), consisting of geometric lines that form an interlaced strapwork” (Wikimedia Foundation, Inc., 2014). Figure 9 is directly from Lu’s paper in Science (2007), and compares how a very common pattern – the decagonal star – seen in this spandrel and many other mosaics, would be constructed using the simple geometric drafting method, versus the use of girih tile templates. The top row (A-D) shows the progressive drafting steps – the basic 10-point star is inscribed in a circle divided into ten equal arcs each of 36° by connecting every 3rd vertex with a straight line. Subsequent steps involve using temporary drafting lines (purple dashed), adding line segments (blue), and erasing line segments (red). Panel E shows the same pattern within a larger mosaic setting, with girih tiles superimposed, and panel F shows the five girih shapes once more, in case you’ve forgotten them.

Over the centuries the geometrical patterns became more and more sophisticated and complex, with many of them displaying two-fold, three-fold, five-fold and higher symmetry, and periodicity. Many of us will remember order of symmetry and repeatability (periodicity) being key properties that help to uniquely define crystals, and indeed many Islamic mosaics have therefore been described as crystalline. In addition, fractal-like properties can also be seen to develop, with similar or different types of symmetries and periodicities at larger scales enclosing others at smaller scales – the pattern in Figure 8 has this characteristic.
What really piqued Lu’s interest were patterns with five-fold and ten-fold symmetry that were entirely non-repeating, i.e. infinite, such as at Isfahan. These have been described as quasicrystalline because they contain symmetries but their patterns never repeat. The increasing sophistication over time, the wide geographical spread of very similar patterns, the lack of compounding errors which one would expect from using a straight edge and compass, the Topkapi scroll (Fig. 10, an apparent medieval instruction kit of sorts) which actually shows girih tile outlines overlying examples of mosaic patterns – all these and other pieces of evidence has been found that complex math was used to derive their shapes; it is most likely that they were empirically derived and refined. Mosaic designers would have had templates of the five shapes in various sizes, to use both in design and to actually guide artisans on site. Wikipedia has an excellent description of the five shapes (Wikimedia Foundation, Inc., 2014). The angles of all edges are multiples of 36°, and each edge is exactly the same length. An important element of the girih shapes is that they would have come inscribed with the straplines; these have to touch halfway along each edge at 54° in their interiors. This means that when the shapes are placed side by side, the straplines all connect in highly interesting ways. In fact, within most mosaics the girih edges are not shown, it is the straplines which carry and dominate the pattern, and the girih tile shapes can only be inferred.

At this point my objectives for the article are met – I’ve highlighted these gorgeous mosaics and their interesting mathematical properties to readers more culturally inclined; to those at the more mathematical end of the spectrum I’ve opened the door to further reading on the complex math involved in the analysis of patterns such as those found in these mosaics, especially the non-repeating patterns.
On a side note, researching this article highlighted to me the dangers involved in reading popular science articles, and even more so in writing them. It is very easy for me to slap together an article by skimming through articles of variable genesis and reliability, and to possibly give an incomplete, or even incorrect understanding of the topic. When I first read the Saudi Aramco World article, among other things, I got the impression that Lu was the first person to apply rigorous mathematics to understand the design of the mosaics, and that most of the mosaics were non-repeating. When I read the more scholarly articles, I found out others had done previous work on the topic, notably Emil Makovicky (Makovivky, 2007) (Makovicky, 1992) and Jay Bonner (Bonner, 2003). Not only are there strong differences in opinion on the topic, but Lu appears to have committed that unforgivable crime (to academics) of not properly acknowledging previous work. I also got a more balanced understanding that most Islamic mosaics are crystalline, and it’s only a few which exhibit quasi-crystalline patterns. All this just goes to show that light and fluffy science articles like mine and others are fine and serve a certain role in popularizing interesting topics, but they are not a substitute for solid, peer-reviewed work.

On a funny side note, Bier (2011) points out that both Lu and Makovicky have mistakenly identified the Gonbad-e Qabud (Blue Dome) tower tomb (Fig. 11) as having eight sides when it clearly has ten! That these mathematical experts can’t even get the number of sides of a huge polygonal tower correct I find really, really funny. As an amateur woodworker, this topic has inspired me to create some routing templates based on girih tiles, with the goal of building some pieces of furniture with non-repeating decorative patterns on them. I’m also left with the question of how these designs were projected so accurately onto curved surfaces, which of course many of the domes and arches are. This non-Euclidean projection adds another dimension in to an already complex math, begging for a new set of patterns yet to be explored.











Share This Column