As a follow up to his excellent September VIG column (Value of Integrated Geophysics, Sept. 2013 RECORDER) Lee Hunt suggested I build an article around Bayes’ theorem. Lee has published an article with some excellent examples of Bayesian methods before (Hunt, 2013), but we thought something fluffier would make for good reading. With input from Lee, I will give a couple of examples of Bayes’ theorem in practice, and also address the larger topic of using logic in the work place (or not). I’d recommend reading Lee’s May article if you haven’t already.
I’ve always assumed that we scientists are a logical bunch, definitely more so than your average person. However, recently – perhaps because I’ve been reading books on topics like heuristics (Thinking, Fast and Slow by Daniel Kahneman) and the science of prediction (The Signal and the Noise: Why So Many Predictions Fail – but Some Don’t by Nate Silver) – I’m questioning this. I see illogical, irrational, emotional decision making all around me in our supposedly logical scientific industry. Just the other day I heard of an interpreter who, following a processing turkey shoot, instead of choosing the company which delivered the highest quality processing (subjective, admittedly, but the result of some quasi-formal evaluation process), chose the one that made his reservoir “look the biggest”. Yikes! Keep this example in mind when you reread Lee’s May RECORDER article, and its observations on how NPV can change depending on the quality of the seismic.

Ironically, the artsy-fartsy, liberal arts crowd we stereotype as illogical is more likely trained in logic than us. Unlike geophysics, logic is a basic component of the arts curriculum, probably covered in Philosophy 101. I suspect that’s one reason why Peter Cary is such an excellent scientist – among his several degrees is a BA in Philosophy. While we scientists may apply logic within strictly mathematical / scientific contexts, I don’t believe that necessarily translates to being logical when faced with less clear cut situations demanding decisions. I’m open to counterarguments, but I am certainly alarmed at times by apparent lack of rigour and logic within our industry.
So how do we avoid these pitfalls? A good first step is to know the enemy – understand what logical and emotional / heuristic pitfalls you are prone to. Second, stick to tried and true scientific methodologies. The use of logic and appropriate methodologies will safeguard against many pitfalls, but many others are created by our innate reliance on heuristics. Heuristic mechanisms are extremely problematic because they kick in BEFORE the logical side of our brains has a chance to do anything. If you kibosh a proposed well because you’re still grumpy from being cut off in morning traffic, Bayes’ theorem isn’t going to help one bit – you have to make a conscious effort to engage the logical part of your brain first to get there. I have covered the topic of heuristics before (Human heuristics, Dec. 2012 RECORDER), so will stick to logical pitfalls here.
A while back I stumbled onto a poster depicting most logical fallacies (Information is Beautiful, 2013). Looking through these 47 fallacies I immediately identified ones I could relate to our industry. I’m going to pick a few of these fallacies out, and give examples that will help illustrate them.
Appeals to the mind
In my career, I’ve seen “Appeal to novelty” play out several times. Back in the 1980’s when AVO first came on the scene, many geophysicists embraced it as if it was the solution to everything. In fact, the enthusiasm around AVO created such high expectations that when dry holes inevitably followed, AVO fell into disrepute for a while. It wasn’t until later when tools (such as Hampson Russell’s AVO software) and a realistic understanding of the method’s limitations caught up with reality that AVO became an accepted seismic tool. I’ve seen the same thing on a smaller scale when it comes processing fads. Anyone remember the Karhunen- Loeve (KL) transform? I suspect the same might be true of certain attributes on the interpretation side.
“Appeal to common practice”, “Appeal to popular belief”, and “Appeal to tradition” all overlap somewhat. I worry that these may be at play in a very general, overarching sense when it comes to the use of seismic in the WCSB. Are we guilty of illogically believing seismic is still of value in this basin just because “it’s always been that way,” or because “of course you need seismic to drill wells,” or because, “obviously we need to have geophysicists – all the other oil companies do”? Smaller examples of these logical errors happen every day. For example, how many times have the acquisition parameters on a new shoot seismic project been based on what was used in the area before? How many times is the seismic interpretation in an area done the same as it was done before? At this year’s CSEG Symposium (2013), one of the speakers – I believe it was David Monk, but it could have been Art Weglein or one of the others – asked why we are still acquiring seismic as if post-stack data was the ultimate and only product.
Faulty deduction
Here again is a rich ground for logical errors we are prone to. For example, I’d hate to speculate how many hours have been wasted at meetings and on projects because of the “Perfectionist fallacy”. I’m thinking of discussions around software design, and subsequent programming efforts. If the goal is always perfection, then how many perfectly reasonable and achievable options have been rejected in pursuit of something that will take far too long to achieve, if ever? Or how about the “Middle ground” fallacy, where two sides with conflicting points of view assume that the correct path forward lies somewhere between their opposing stances, when in fact the best option may lie outside that extremely limited plane?
A favourite of mine is the “Design fallacy”, the belief that because something (an idea, concept, thing, plan, etc.) is attractive in some way(s) it is more true or valuable than alternatives that do not appear so appealing. This is one reason that seismic processing methods over the years have evolved and developed to take care of all those cosmetic issues that really don’t have any relationship to the quality of the image. The reality is that if an interpreter has two sections in front of him/her, and one has some annoying cosmetic flaws like spikes down near the end of record, well below basement, the chances are that it will be deemed less reliable than the one without the spikes. Perceptions of software can be affected by this too: if a program has really pleasing graphics, is easy to navigate, and so on, it is more likely to be perceived as scientifically reliable, even if the underlying algorithms are flawed.
“Hasty generalisation” – basing conclusions on an unreliably small number of samples – and “Jumping to conclusions” – making decisions without using all available information – are the bane of anything interpretive. While I’m not privy to what goes on between a seismic interpreter and his/her workstation, I’d bet dollars to donuts that there’s a whole lot of this going on in Calgary oil company offices.
I’d like to mention the “Gambler’s fallacy” here briefly, which can be boiled down to a belief that previous outcomes affect future outcomes. Being prone to this type of thinking would appear antithetic to the role of the geophysicist, but maybe it isn’t. In most drilling situations previous outcomes are highly relevant to future wells; a good example would be drilling step out wells – each successive well is obviously not a roll of the dice. On the other hand, some a priori information is irrelevant, and you don’t want drilling decisions made by people displaying the irrational sort of behaviour seen at casinos.
Appeal to emotions
I believe that most of these fall into the area of heuristics, but I’d like to mention one, “Appeal to wishful thinking”, as it brings to mind something I’ve seen many times. What I’m talking about is sitting at a talk viewing slides of cross plots, and seeing what looks to me like a random cloud of points, kind of like those clusters of insects you might ride into along the Bow River on a summer evening, and which end up in your eyes and teeth. How many times have you seen this, only to hear the speaker with total confidence describe the straight line going through the cloud as being a good fit?! Or multi-attribute displays that look like Rorschach tests being confidently interpreted (Why do I always see my mother, and not the seismic expression of the drilling target??) I think we are often guilty of falling in love with a particular outcome or interpretation, because we oh so want it to be true.

On the attack
Along with the previous category “Appeal to emotions”, I think this area falls into the field of heuristics. Readers will be familiar with many of these illogical tactics – “Straw man”, “Burden of proof”, “Ad hominem”, etc. I see them playing out every day in current high level public debates, notably on global warming, terrorism, pipelines, oil sands, etc. I don’t believe they are really an issue in the field of geophysics, other than perhaps nasty stuff going on around boardroom tables, and sometimes when disagreements between technical experts get personal.
Manipulating content
This is a disturbing category of fallacies, and I suspect that if any of them are an issue in geophysics, they are likely the result of other fallacies or heuristics. For example, I don’t think any geophysicist is out there “Begging the question” or “Suppressing evidence” in a calculating way, but they may end up doing so because of things like the “Appeal to wishful thinking” mentioned above. What I mean is, they might be so in love with a particular interpretation that they subconsciously suppress or avoid any information that might go against it. Think back to our friend who chose the processing that made the reservoir look the biggest – seems like a pretty good fit, doesn’t it?
One fallacy I sometimes remind myself to be wary of is “Misleading vividness”, particularly when I’m explaining seismic processing pitfalls to interpreters. When highlighting the possible risks associated with a particular process, it is easy to convey the impression that it is a common risk. In fact, most seismic processing projects are executed with few or no problems, and errors and risks are rare.
One kind of funny fallacy I believe many interpreters might find themselves stumbling into nowadays is “Unfalsifiability”. It seems many interpreters are being kept around more or less on standby, in the expectation that gas prices will improve and exploration and drilling budgets will increase. In the meantime, many of them are busy stockpiling drilling locations. I suspect a belief that many of these locations will never be drilled is luring interpreters towards “creative” interpretations.
Garbled cause and effect
I’ve left this category for last because I believe many of the fallacies in here are of the type that can be avoided by methods such as Bayes’ theorem, and as such I will go into more detail.
Affirming the consequent
This is an extremely common error – assuming that there is only one explanation for an observation. I see it all the time when processors troubleshoot, and I suspect it happens frequently with interpretation as well.
Circular logic
I’m struggling to think of a good example here, but I’m sure readers can. I suppose I could go back once again to our hapless interpreter. Essentially he is employing circular logic by choosing the one version of processing: “This seismic is showing that the reservoir is the biggest, therefore it is the most correct, and because it is the most correct then my reservoir must be big.”

Cum hoc ergo propter hoc
I see this one all the time – when a cause and effect relationship is drawn between two events that occur together. We all do it in a superstitious way: “I jinxed my chances at getting that promotion by telling my friends about it.” But does it affect our work decisions? I suspect so, without us being aware of it.
Denying the antecedent
This is the assumption that there is only one explanation for an outcome, and it is a really huge pitfall within geophysics. Many of the inverse problems we are trying to solve are underdetermined, and outcomes can usually be explained by more than one set of circumstances. Yet we do tend to treat the answers our algorithms and interpretations give us as being correct.
Ignoring a common cause
This is only subtly different than several of the preceding fallacies. It is the claim that when two events commonly occur together, then one must be the cause of the other. I’m thinking back to when we were drilling every bright spot under the assumption that a gas sand was the only possible explanation, when of course there are other causes for bright spots, such as tuning effects.
Post hoc ergo propter hoc
Again, this one is only slightly different than some of the others. It happens when a causal relationship is inferred from one event following another. I’ve seen this type of thing happen. E.g. “As soon as we updated the OS, we started seeing spikes in the decon output. There must be a bug in the new OS.” Meanwhile of course, something else may be the explanation – a slight change to the decon code, one crew out in the field with faulty instruments, whatever...
Two wrongs make a right
This is a natural human reaction when things go wrong. “We’ve drilled three bad wells on seismic. We are not going to use seismic anymore!”
Bayes’ theorem
Bayes’ theorem provides a safeguard against the effects of false positives and compounded uncertainty, blind spots in human reasoning. These pitfalls are a combination of some of the fallacies discussed above, notably most of those under “Garbled cause and effect”. Let’s look at a couple of examples.
Your blood test comes back with a positive for cancer. “Oh my god,” you think, “I’m going to die!” Well, not so fast. Let’s say the actual occurrence of that type of cancer is 0.1%, i.e. one out of every 1,000 people will get it (so 999 won’t), and further, 90% of the time the blood test accurately detects the cancer, but 5% of the time it detects cancer when it’s not actually there, i.e. a false positive. For every 1,000 people given the blood test, 5% of those 999 people will get a positive test (which is false), so almost 50 people; 90% of the time that one unfortunate soul who actually has cancer will get a positive test. What this means, counterintuitively, is that if you receive a positive blood test indication that you have cancer, it is almost 50 times more likely that it is a false positive and you don’t have cancer, than you actually do have cancer.
Mathematically, Bayes’ theorem is given by,
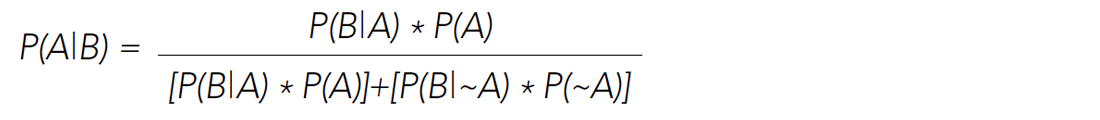
or

where,
P(A) is the probability of A
P(~A) is the probability of not A
P(B) is the probability of B
P(A|B) is the probability of A given B
P(B|A) is the probability of B given A
I find this notation confusing, but it’s actually quite simple and makes sense if you think it through. The numerator is the number of true positives, and the denominator P(B) is the total number of positives both true and false, and their ratio gives the probability of a positive test being true, in our example the chance of actually having cancer given a positive test.
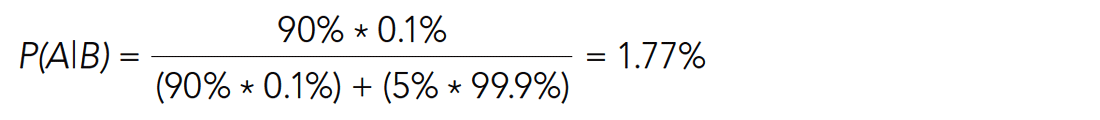
To spice things up, let’s apply this to a more uplifting example, the probability of a young geophysicist’s evening at the bar resulting in a happy ending, given he/she hits it off in flirtatious conversation with someone.
Let’s just use these estimates:
P(H) is the a priori probability of happy ending = 5%
P(~H) is the probability of going home alone = 95%
P(F) is the probability of flirtatious bar conversation
P(H|F) is the probability of a happy ending following flirtatious bar conversation
P(F|H) is the probability of flirtatious bar conversation preceding a happy ending = 99%
P(F|~H) is the probability of flirtatious bar conversation preceding a lonely night = 50%
Applying Bayes’ theorem would tell our romantic young scientist the following:
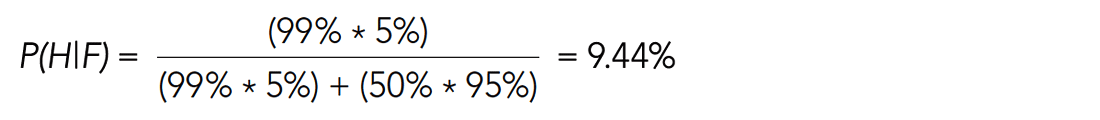
Given that most of the time as a young man I never even got to the flirtatious conversation part (if ever!), this has me thinking that all those years of lining up in the cold to get into really loud crappy bars, only to wake up alone with a headache, were probably not time well spent. I should have been working out the probabilities at other venues, like maybe church. The logical trap we humans fall into is that we latch on to an apparent causal relationship between the outcome and the test (in this case we think flirtatious conversation = sex, 99% of the time!), but ignore the overall probability of the outcome (the dismal truth that 95% of bar goers end up home alone), and the incidence of false positives (all those charming shouting conversations in bars that go nowhere), which change the probabilities such that even if you get as far as engaging in witty bar talk, you’ve still got less than a 10% chance of getting lucky.
Let’s leave the bar scene and get back to work. In this environment the interpreter can be seduced by the fact that a very high number of producing wells in an area were associated with some kind of positive seismic indicator. Ignored are the overall drilling success rate in the area and the rate of false positives, that is dry holes drilled on positive seismic indicators. Our young geophysicist could very well end up being unlucky at both love AND with the drill bit!
I’ve related the importance of deploying proper logic at work. I think if you go back now to Lee Hunt’s article in the May 2013 RECORDER, you will clearly see how applying Bayesian methodologies can help the geophysicist add value. As scientists, the challenge is for us to apply critical thinking and the scientific method to our work, typically in the form of quantitative testing and analysis; anything else amounts to nothing more than witchcraft (no offence to witches). The question the reader is left with is, do you want to add value and be a scientist in your professional role, or do you want to be a shaman?
Key search words
Bayes, logical fallacy
References
Hunt, L. (2013, May). Estimating the value of Geophysics: decision analysis. CSEG RECORDER, 38(5).
Information is Beautiful. (2013). Rhetological Fallacies. Retrieved July 9, 2013, from Information is Beautiful: http://store.informationisbeautiful.net/product/ rhetological-fallacies
Kalid. (2007, May 6). An Intuitive (and Short) Explanation of Bayes’ Theorem. Retrieved October 11, 2013, from Better Explained – Learn Right Not Rote: http://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/
Wikimedia Foundation, Inc. (2008, February 21). Rorschach test. Retrieved October 14, 2013, from Wikipedia: http://en.wikipedia.org/wiki/ File:Rorschach_blot_10.jpg
Wikimedia Foundation, Inc. (2013, October 5). Bayes’ theorem. Retrieved October 11, 2013, from Wikipedia: http://en.wikipedia.org/wiki/Bayes’_theorem











Share This Column