A while back my 8-year son asked me why we can never see the other side of the Moon. I described the situation to him, but couldn’t give him any “whys”, leaving us both somewhat frustrated. More recently, CSEG member Jeff Beckett suggested this very topic would make a good article, as we are all aware of the Moon’s rotational relationship with the Earth, but probably most of us are unaware of (or have forgotten) the mechanics behind it.
To explain things requires delving into the world of planetary bodies, satellites, orbits, etc. Things get complicated fast, as is the case in most branches of science. As usual I will attempt to stay high level.
The reason one half of the Moon is always facing away from Earth is explained by synchronous rotation, and tidal locking. Synchronous rotation is easily confused with synchronous orbit, which is more relevant to man-made satellites, so I will cover both topics. I will dispense with definitions and descriptions that are more correct in the general sense, and will instead use words such as planet, satellite, etc. for the sake of readability.
Synchronous orbit
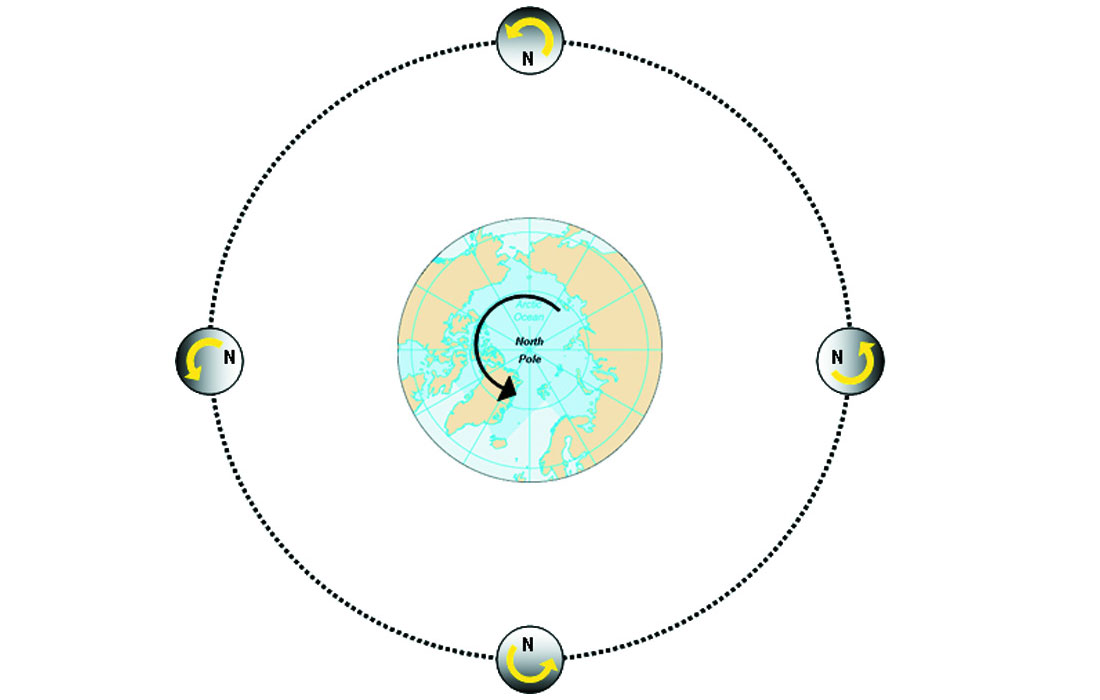
A satellite is said to be in synchronous orbit about a planet if the period of the satellite’s orbit around the planet is exactly equal to the rotation period of the planet (i.e. the length of its sidereal day: one day plus one night), and the direction of the satellite’s orbit is the same direction as the rotation of the planet (Figure 1).

Many human-made satellites are purposely put into synchronous orbit. What this means is that a satellite in synchronous orbit will more or less stay above the same point on Earth. I say more or less because there are actually a few types of synchronous orbits.
The term geosynchronous orbit is a more specific term referring to satellites in synchronous orbit around our Earth, the prefix geo- indicating this, geo being the Greek root for earth. A satellite in geosynchronous orbit will be above the exact same point, or the exact same time, each day. The semi-major axis for all geosynchronous orbits is 42,164 km, given by the equation,
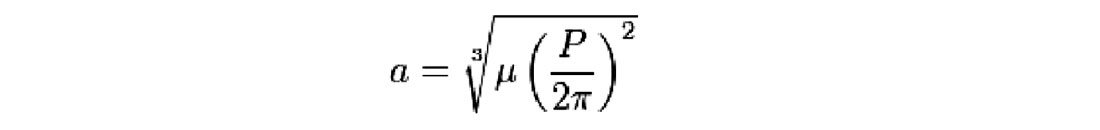
where
α is the semi-major axis,
μ is the geocentric gravitational constant, and
P is the orbital period, which is one day for all satellites in geosynchronous orbit about the Earth.
A satellite that remains motionless relative to a point above the Earth’s equator is said to be in a geostationary orbit; this type of synchronous orbit is both circular and equatorial. In other words it is a specific type of the more general geosynchronous orbit.
A satellite that is in a non-equatorial synchronous orbit will oscillate north and south above a fixed point on the Earth’s equator. A satellite in an elliptical synchronous orbit will appear to oscillate east-west. If a satellite is in an orbit that combines both these characteristics, from the Earth it will appear to oscillate both north-south and east-west, and will describe a figure eight movement known as an analemma. Many maps and globes display an analemma, but in that case it is a diagram indicating the Sun’s position as viewed from a fixed point at a fixed time (usually noon, at Greenwich or somewhere significant) over the course of a year. The Earth being a satellite of the Sun, this of course is entirely consistent with our discussion of man-made satellites rotating around the Earth, just that for the former case the observer is on the satellite (Earth); with the latter case the observer is viewing the satellite.
Man-made satellites are subject to a variety of effects that cause them to deviate from their ideal planned orbits. These factors include solar wind, gravitational effects from the Sun and Moon, variations in the Earth’s gravitational field, radiation pressure (especially from the Sun), etc. To counteract these effects, thrusters are employed on the satellites, to periodically nudge them back into orbit.
One type of non-synchronous orbit satellites are placed in has been given a somewhat macabre name – the graveyard orbit. This is actually a supersynchronous orbit – the orbit takes longer than one sidereal day on Earth. Satellites are moved out to this orbit, a few hundred km further away from Earth, when they are nearing the end of their useful lives. The idea is that they are thus removed from interfering with active satellites operating at the geosynchronous orbit range. If we can move these aging satellites a bit further out to protect newer satellites, why not just de-orbit the old ones entirely? The reason is that satellites don’t have the power to do so, or it would not make economic sense to use so much of the available power to banish them to outer space. Moving a satellite from geosynchronous orbit out to graveyard orbit takes a Δv of approximately 11 m/sec., requiring about 3-month’s worth of normal operational power. To de-orbit a satellite would take a Δv of approximately 1500 m/sec.
Our Moon is obviously not in synchronous, or more specifically geosynchronous orbit about the Earth. The period of its orbit around the Earth is not the same as our sidereal day; in fact, it takes the Moon about 27.3 of our days to complete one orbit of our Earth. Consequently the Moon rises and sets at different times each night, and if we were to stand in the same place at the same time each night we would see its position progressively shift a bit each night. So the aspect of the Moon’s far side always facing away from us is not related to synchronous orbit, but it is explained instead by something with a very similar name, but which is actually quite different; synchronous rotation.
Synchronous rotation
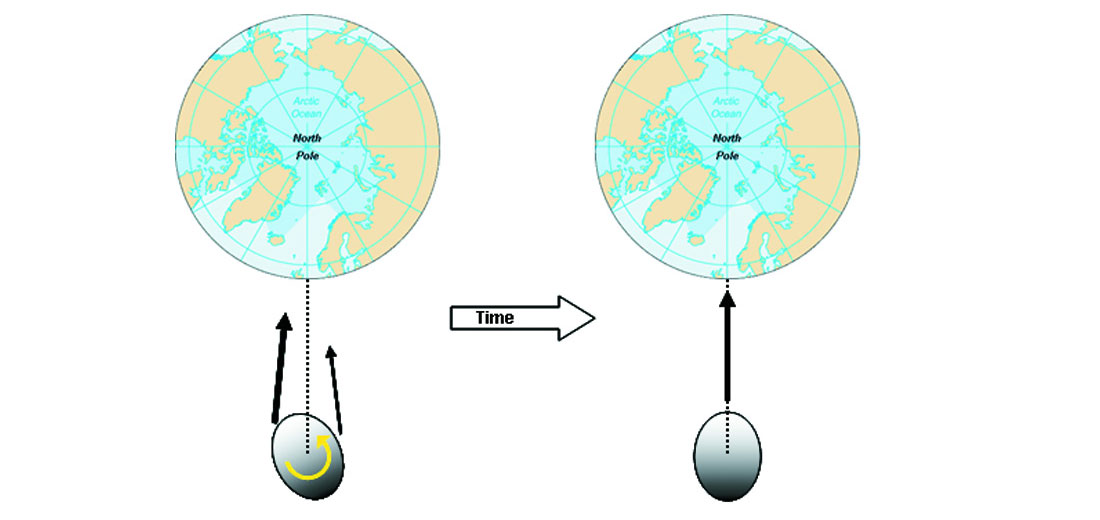
A satellite is said to be in synchronous rotation if it takes the same amount of time to rotate once about its axis as it does to complete one orbit around the main planet. So whereas with a synchronous orbit where the period of the satellite’s orbit is the same as the period of the planet’s axial rotation, with a synchronous rotation the periods of the satellite’s orbit and axial rotation are the same (Figure 2). The implication of synchronous rotation is that the hemisphere of the satellite will always face away from the planet, the exact situation we have with the Earth and its Moon.
So the question is, why is this the case? It would seem statistically improbable that the period of the Moon’s rotation was exactly the same as the period of its orbit around earth, given the infinite number of other possibilities. It is indeed not coincidental, and in fact throughout the viewable universe many, or most, moons (of a significant size) rotating about planets display synchronous rotation. The explanation lies in a phenomenon known as tidal locking.
Our Moon
It is estimated that our moon was formed about 4.5 billion years ago; a mere blink of a galaxial eye (40 or 50 million years) after our solar system was formed. There are various theories explaining or describing the Moon’s formation. Three are currently out of favour, mainly because they do not adequately explain the high angular momentum of the Earth-Moon system:
- Centrifuge theory – the Earth’s spin flung off the material (sometimes used to explain the Pacific Basin as the hole left behind) that formed the Moon. Two flaws with this theory are, first, that the Earth’s spin would have had to have been improbably high to fling off material like that, and second, this centrifugal process would logically leave the Moon’s orbit within the Earth’s equatorial plane, which it is not.
- Concurrent formation theory – the Earth and Moon somehow formed out of the same primordial material via some kind of complicated asymmetric accretionary processes. A flaw with this theory is that the composition of the two bodies is quite different; most notably the Earth contains far more iron.
- Capture theory – the Moon was formed somewhere else, and as it floated by the Earth was pulled in by its gravitational field and captured into an orbit around Earth. The flaw with this is that the mass of the Earth relative to the Moon’s is not great enough to pull off this “capture” maneuver.
Currently in favour is the impact theory. This postulates that a large body (planet size), that proponents of this theory call Theia, smashed into the proto-Earth. This impact sent a huge volume of fragmentary material into an orbital debris cloud around the Earth. Over time accretionary processes formed the Moon. There are no major flaws with this theory, but there are certainly details missing, or still to be worked out, especially related to the relative proportions of Earth and Theia material within the Moon.
The key point to carry on to the next section is that this proto- Moon was spinning much faster than it currently does.
Tidal locking
So we have a situation over 4 billion years ago with our proto- Moon, spinning very quickly on its axis, in orbit around our primitive, lifeless planet Earth. The Moon is large enough (just under 3500 km in diameter) to experience significant deformation caused by the gravitational pull of the Earth, which is much more massive than the Moon (81 more times massive).
This gravitational deformation would manifest itself as a big bulge facing directly towards the Earth, in the absence of any spin. But now factor in the spin of the Moon, and imagine that the spin is fast enough that the bulge is always spinning a bit ahead of the gravitational force’s ability to pull it (the bulge) into line with the Earth-Moon axis. The reason the bulge is ahead of the Earth-Moon line is that the crust would have been non-fluid, as it still is, and could thus not deform quickly enough to be “left behind” by the rotation. We now have the conditions necessary for tidal locking to come into play. With more mass on the “bulge side” than the opposite, there is a differential gravitational pull on the Moon. In essence, this creates a torque on the Moon in the opposite direction as its spin, which effectively dampens the spin. Over a relatively short period of time, estimated at just a thousand years or less, this torque would have slowed down the Moon’s spin until its period was the same as the period of its orbit around Earth.
The previous paragraph is a simplification which I will now elaborate on. There are actually two bulges produced by gravity. This is because the side of the Moon closest to the Earth experiences the greatest gravitational pull since it is closest. The far side of the moon experiences the least gravitational pull, therefore there is also a smaller bulge facing directly away from the Earth. Associated with this is a relative compression in the plane perpendicular to the axis between the two bulges. Another way of looking at it is that the gravitational gradient imparts an egglike shape on the Moon. If you revisit the last paragraph, you will see that the dampening effect on the spin, resulting in tidal locking, is actually caused by the net difference in gravitational pull on the closer, bigger bulge, and the farther, smaller bulge (Figure 3).
In a certain sense one could say that within the Earth-Moon system, the Moon is no longer spinning. It is as if it is solidly connected by a spoke to the centre of its orbital rotation, the centre of the Earth. From this point of view it is the Earth that is spinning away on its axis, much like those silly trick hubcaps that keep spinning even when the vehicle is stopped.
Taking the tidal locking model further, one would expect that the Moon, and indeed all other satellites in synchronous rotation, would stabilize to a deformed, non-spherical ellipsoidal shape, with the axis of elongation pointing directly towards the Earth. This is in fact the case. Furthermore, it would not be surprising to expect higher density material facing the Earth, and lower density material facing away from the Earth. Some scientists have pointed to this to explain the preponderance of heavier basalts known as lunar maria on the near side of the Moon. (The word maria comes from the Latin mare, meaning sea, as early astronomers believed the easily visible dark patches on the Moon to be seas.) Approximately 31% of the near side’s surface is maria, while only 2% of the far side is maria. However, this does not withstand scrutiny as the maria formed, via volcanic eruptions triggered by meteor and comet impacts, about 1 billion years after the Moon achieved synchronous rotation. One must remember that the Moon is subject to its own gravitational field also, not just the Earth’s pull, so denser components are also more likely to be found closer to the centre of the Moon.
But why are the maria essentially found only on one side? There must be a reason beyond chance. Lunar probes have found a much higher concentration of heat-producing elements on the near side, explaining why there was more volcanic activity on the near side. Perhaps this higher occurrence of heat-producing elements is a gravity-induced effect that took a while to fully develop. Anyway, my hunch is that there are gravity- and synchronous rotation-related explanations still to be discovered for most or all of the Moon’s observed nearside / far-side asymmetrical characteristics.
Finally, will the Earth become tidally locked to the Moon? Eventually, yes. What this would mean, assuming humans are still around, is that the people on one of Earth’s hemispheres would never see the Moon. With the Earth spinning at a greater frequency than the Moon orbits us, it is subject to tidal locking itself. Along with our ocean tides, the Earth also experiences earth tides, i.e. deformation. The length of our day is gradually getting longer, as the Earth spins slower and slower. Over geologic time it is estimated that the length of our day has gone from 18 hours to 24 hours. The reason it is taking so long for the Earth to become tidally locked with the Moon is that because the Earth is so much more massive than the Moon, the tidal locking torque effect relative to the Earth’s angular momentum is so much smaller. When the two bodies in question are close in mass, tidal locking will occur at a similar rate in both. Pluto and its similarly-sized satellite Charon became tidally locked to each almost at the same time.
If the satellite’s orbit is eccentric, then tidal locking mechanisms can result in orbital resonance, where the ratio of the rotation period to the orbital period is a simple fraction other than 1:1. In fact, one could view synchronous rotation as the specific 1:1 ratio case of orbital resonance. The best known example of orbital resonance is Mercury, which spins three times on its axis for every two rotations around the Sun – in other words the aforementioned ratio is 3:2.
Far side of the Moon
Many of my generation spent hours in basements, in dubious states of coherence, listening to Pink Floyd’s album Dark Side of the Moon. Purportedly the album is held together by a lunar theme, more specifically the “dark” side of the Moon. In reality the far side of the Moon receives as much sunlight as the near side. The first time humans ever saw images of the far side occurred in 1959, when the Russian space craft Luna 3 orbited the Moon. Imagine that! No humans had ever seen the far side prior to 1959. Figure 4 is an image of the far side of the Moon taken from the American space craft Apollo 16.

Humans being humans, over the centuries there has been considerable speculation and fabrication regarding what was to be found on the far side of the Moon. In Europe this beguiling and intriguing unknown, and obsession with it, became linked with madness, hence the derivation of the word lunatic. I recall one track from “Dark Side of the Moon” containing the maniacal cacklings of a madman. Perhaps in billions of years all the people on the far side of the Earth will be called lunatics, since they will always be obsessing about the Moon just over the horizon that they can’t see.











Share This Column