Letters to the Editor

More Reflections on Q

In their recent RECORDER article “Reflections on Q,” Lines at al. (2008) touched on two of the most fundamental problems which are of great interest to seismologists – namely the origin of seismic reflectivity, and its relation to the impedance and absorption. In the problem of absorption, its perceived dependence on the frequency is particularly important yet also most enigmatic. Because such theoretical subjects do not receive adequate attention in today’s applied-geophysics curricular and are often taken for granted, I would like to offer a couple of comments on them here.

First, despite the simple paradigm implicitly accepted by most practitioners, the seismic impedance is not merely a product of wave velocity and medium density. The impedance in elastodynamics and acoustics is the ratio of stress (pressure, traction) to particle velocity in the seismic wave (Aki and Richards, 2002). From this definition, at normal incidence, P-wave impedance in an absorptive medium is:

as shown by Lines et al. (2008). Thus, contrasts in Q modify the impedance and cause phase-shifted reflections, although relatively weak because the values of Q are typically much higher than 1. Note that by virtue of the general definition of Z above, the familiar formula for the reflection coefficient from a boundary of two layers:

holds in all cases and for all types of waves.

My second comment inspired by the aforementioned paper relates to the widespread notion that Q should necessarily have a frequency dependence in absorptive media. However, there also seems to be little data reliably corroborating this conjecture in the exploration frequency band. I have spent a significant effort looking for the origins of such a belief, and discussed it with many seismologists. There appear to be two main reasons for such an assertion: 1) the Kramers-Krönig equations relating the velocity dispersion to Q, and 2) common observations of Q(f) in long-range (crustal and global) seismology. However, careful examination of these arguments shows that neither theory nor observations actually require Q to be frequency dependent anywhere within the seismological frequency band! Let us quickly look into these two points.

The Kramers-Krönig formulas are integral identities relating the real and imaginary parts of the refraction index, which are required by causality. They are very general and basically correlate the behaviours of the phase velocity and Q at very low and very high frequencies. From these relations, Futterman (1962) showed that the absorption coefficient cannot remain linear (i.e., Q stay constant) at all frequencies – otherwise the observed refraction index (i.e., the velocity) would become negative. However, for values of Q ⊕ 30 or higher, Futterman’s argument only required that Q^-1 should drop at frequencies below about 10-99 Hz! This has of course no practical significance for any seismology – exploration or global, and therefore the Kramers-Krönig relations should not keep us from questioning whether Q is actually frequency-dependent.

In regards to the observations of frequency-dependent seismological Q(f), they are indeed widespread today. Crustal and coda Q(f) often increases almost proportionally to the frequency and sometimes even faster. Numerous theories and models have been advanced in support of such observations (e.g., Liu et al., 1976; Sato and Fehler, 1998). However, revisiting the postulates underlying the Q(f) measurement techniques shows that theoretical models may often run somewhat ahead of the observational constraints. Many presentations of Q(f) have been influenced by the prevalence of particular models, especially of those based on random scattering. However, it is important to realize that in frequency-dependent Q(f) observations, we always deal with the apparent Q which still needs to be carefully related to the corresponding in situ material property.

To see the danger of over-interpreting the apparent Q(f), consider the relation from which it is typically measured:

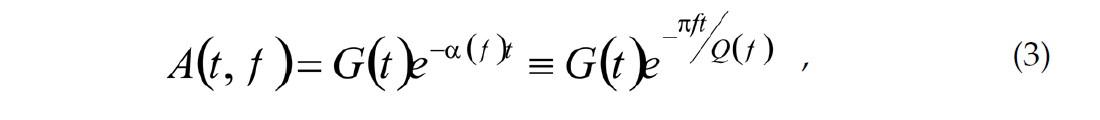
where t is the time, f is the frequency, A(t, f) is the seismic wave amplitude, G(t) is the geometrical spreading, and α(f) is the attenuation coefficient. In this expression, G(t) is typically considered as known, and therefore Q(f) is inverted from the spreading-corrected ratio of A(t, f)/G(t). However, note that when Q ∞ f is found, the attenuation coefficient α(f) becomes frequency-independent, which should better be attributed to an error in G(t). Thus, a positive frequency dependence of the apparent Q(f) can likely be caused by geometrical spreading. This seems to be observed most often.

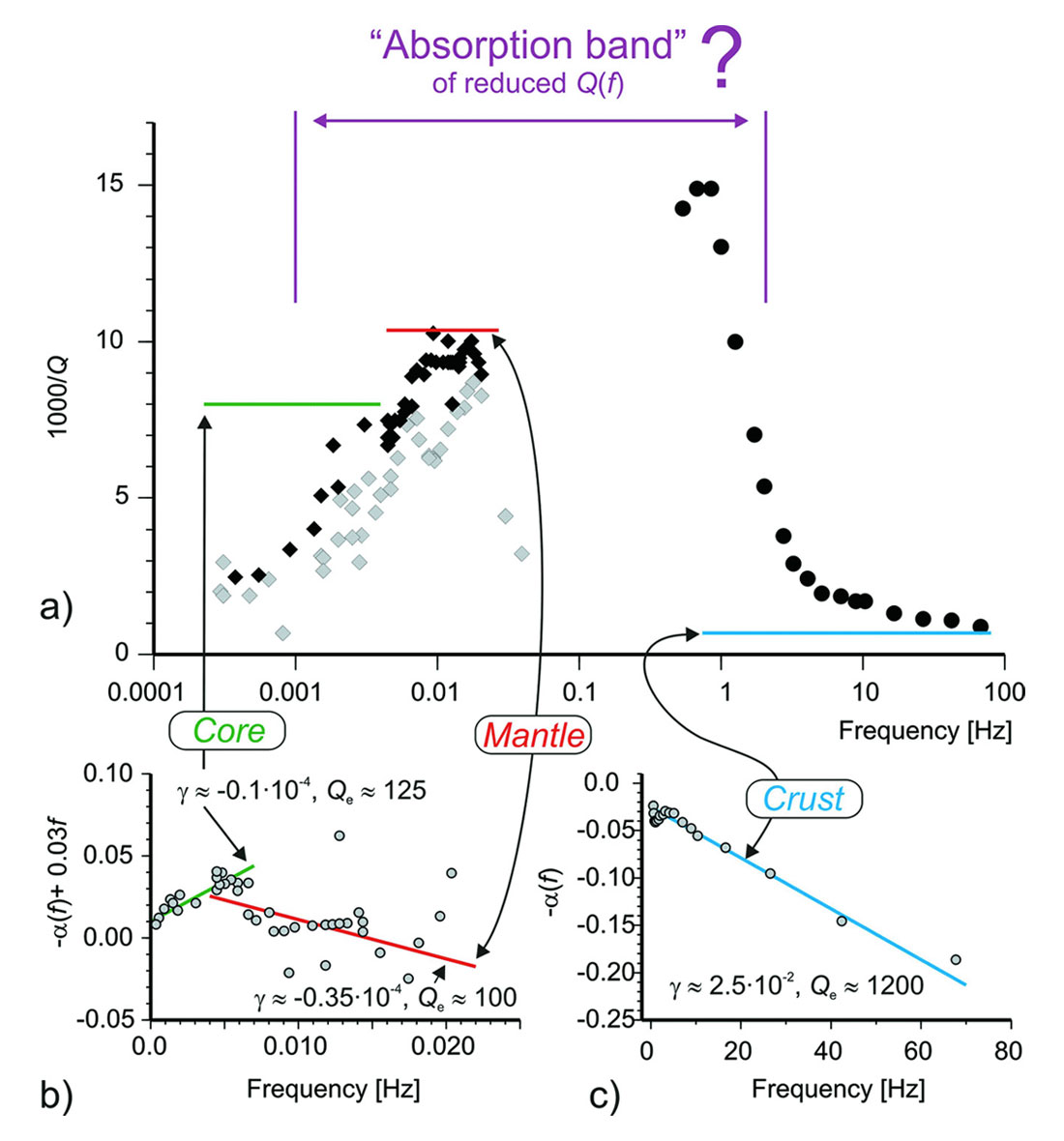
The key support for the frequency-dependent seismological Q idea could come from broad-band Q^-1(f) observations like those summarized in Figure 1a. The values of Q^-1 exhibit a band-limited increase which was interpreted as caused by a frequency band of increased absorption within the mantle (Anderson and Given, 1982). However, as shown in eq. (3), in observations one should better rely on the observed attenuation coefficient α(f) rather than on the apparent Q(f). Reconstruction of α(f) from Q^-1(f) data shows that the α(f) dependencies are in fact linear within the data scatter (Figure 1b, c):

with the linearity within the crustal body-wave band being particularly clear (thick lines and labels in Figure 1). The two breaks in the intercepts and slopes of α(f) should be caused by changing wave types (e.g., surface to body waves) and depths of sampling. The apparent “absorption band” (Figure 1a) seems to be caused not by frequency-dependent absorption but by the mantle and core modes spreading slower (γ < 0 in Figure 1b) and crustal waves –faster (γ > 0; Figure 1c) than predicted by the corresponding geometrical-compensation models. Frequency-independent Q_e ≈ 125 within the outer core, ~100 within the upper mantle, and ~1100-1200 within the crust are sufficient to describe the entire band from ~10^-3 to ~100 Hz. Many additional examples in the 1-30 Hz frequency band were also given in Morozov (2008). Of course, because of strong crustal variability, much more data is still desirable at exploration seismic frequencies.

Thus, both theoretically and experimentally, the entire seismological band may still have a frequency-independent Q. If this is indeed true, measurement and interpretation of Q would simplify dramatically; however this fact can only be established from observations. We should keep an open mind regarding even “classic” models and interpretations and be not prejudiced in favour of a certain paradigm. Data should be the final arbitrator, and I hope that the strong culture of experimental technology would allow exploration seismology to provide the ultimate solution to the problem of the existence of frequencydependent Q in the in situ Earth materials.

References:

Abercrombie, R. E., 1998. A summary of attenuation measurements from borehole recordings of earthquakes: the 10 Hz transition problem, Pure Appl. Geoph, 153, 475-487.

Aki, K., and Richards, P. G., 2002. Quantitative Seismology, Second Edition, University Science Books, Sausalito, CA

Anderson, D. L, and Given, J. W., 1982. Absorption band Q model for the Earth, J. Geophys. Res., 87, 3893-3904.

Futterman, W. I., 1962. Dispersive body waves, Journ. Geophys. Res., 67, 5279-5291.

Lines, L., Vasheghani, F., and Treitel, S., 2008. Reflections on Q, RECORDER, Dec 2008.

Liu, H. P., Anderson, D. L., and Kanamori, H., 1976. Velocity dispersion due to anelasticity: implications for seismology and mantle composition, Geophys. Journ. R. Astr. Soc. 47, 41–58.

Morozov, I., 2008. Geometrical attenuation, frequency dependence of Q, and the absorption band problem, Geophys. J. Int., 175, 239-252.

Sato, H., and Fehler, M. 1998. Seismic Wave Propagation and Scattering in the Heterogeneous Earth, Springer-Verlag, New York.