Expert Answers

Question

Does Parabolic Radon transform multiple removal hurt amplitudes for AVO analysis?

Answer 1

It sounds a simple question but the answer is never a simple yes or no. This underlies most of the questions we face in seismic data processing activities. Do we ever see a process, method or technique that positively answers all our questions? Almost never, right! So, a more appropriate question to ask would be: When or How can we effectively apply Parabolic Radon transform for multiple removal without hurting the amplitudes for AVO analysis?

I will refer to The Leading Edge article Toward true amplitude multiple removal, Jan., 1999 by Nurul Kabir and Kurt Marfurt for most of my comments and remarks. This article clearly illustrates the element of the parabolic Radon transform that affects the amplitude for AVO analysis. The forward and the inverse Radon transforms are not exact inverses of each other. The most commonly used least-squares implementation generates some artifacts which affect the amplitudes at the near offsets (Figures 7 through 10). The far-offset artifacts are more easily handled with some offset tapering (Figures 4 and 5). Even the more advanced implementation of weighted least- squares or high resolution Radon transform is not completely free from these artifacts (Figure 6).

For AVO analysis, intercept (the amplitude at zero-offset) and gradient of the amplitude with offset are the parameters most commonly used. Synthetic and field data examples in the above article clearly illustrate that the mid- to far- offset amplitudes are not significantly affected by the parabolic Radon based demultiple process. The gradient parameter computed over (sufficiently smoothed) mid- to far- offset amplitudes is expected to be a reliable gradient parameter. However, a reliable estimate of the intercept parameter, based on the near offset amplitude, remains a challenge because of the near offset transform artifacts (Figures 7 through 10, Figures 14 and 16). Special care would be needed for the reliable estimation of the intercept parameter.

For field data, the very near offsets are missing due to the acquisition limitations. Interpolation to zero offset with proper amplitude is a great challenge in itself. Least-squares parabolic Radon transform also assumes a uniform trace geometry and amplitude in the offset direction. Field data not only defy these restrictions but are also very often infested with various types of coherent or incoherent noises. Some kind of amplitude regularization before doing the Radon transform may be useful in certain situations. The gain function may be removed later. Some type of amplitude calibration for the near offsets using well information may be necessary for a reliable estimate of the intercept parameter.

For noisy field data, avoiding the very near offset traces may also provide a practical solution.

All the examples in the above article show illustrations of premigrated gather amplitude analysis. But the application of the parabolic Radon transform to post migrated gathers is also very common. The parabolic Radon transform exploits one of the robust discriminants, the moveout discrimination, between primaries and multiples. The parabolic Radon transform is an effective tool for multiple suppression when a moveout discrimination between the primaries and multiples exists.

Parabolic Radon transform has been widely used in the industry for about a decade now for dealing with multiples at various levels of processing, both pre- and post -migration. This tool will continue to find its wide application because it exploits a robust discriminant between primaries and multiples.

Nurul Kabir
Exploration and Production Technology Group
BP, Houston, USA

Answer 2

Multiple removal via the parabolic Radon transform

Since its introduction (Hampson, 1986) move-out based multiple removal via the parabolic Radon transform has been widely applied. The principle is quite simple: in a CMP gather it is expected that a primary and a multiple have a different move-out. If we apply NMO correction to the CMP gather which flattens the primary, the multiples will show a residual move-out. Under the assumption that these residual move-out curves can be approximated by parabolas, the parabolic Radon transform will map them into different areas in the parabolic Radon domain. Muting the area where the multiples are mapped, and applying an inverse Radon transform gives an estimate of the primaries.

The forward parabolic Radon transform of a CMP gather d(x,t), where x represents the offset, can be written as follows:

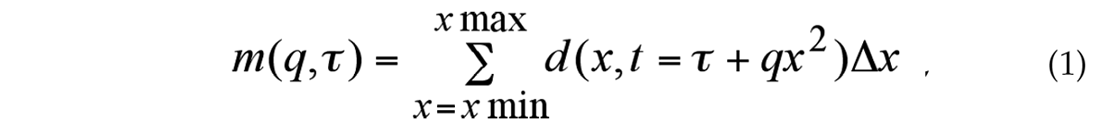
which means stacking the data along parabolic trajectories, where q represents the curvature of each parabola, τ the apex time, xmin and xmax represent the minimum and maximum offset in the data and Δx the offset spacing. The inverse transform can be written as a modeling of parabolas, meaning that each sample in the Radon space represents one parabola in the input space:

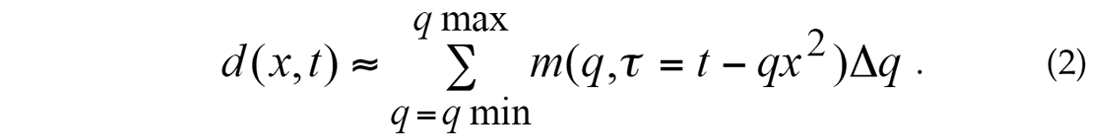
The approximation sign is chosen, because the second equation does not describe an exact inversion of the first equation.

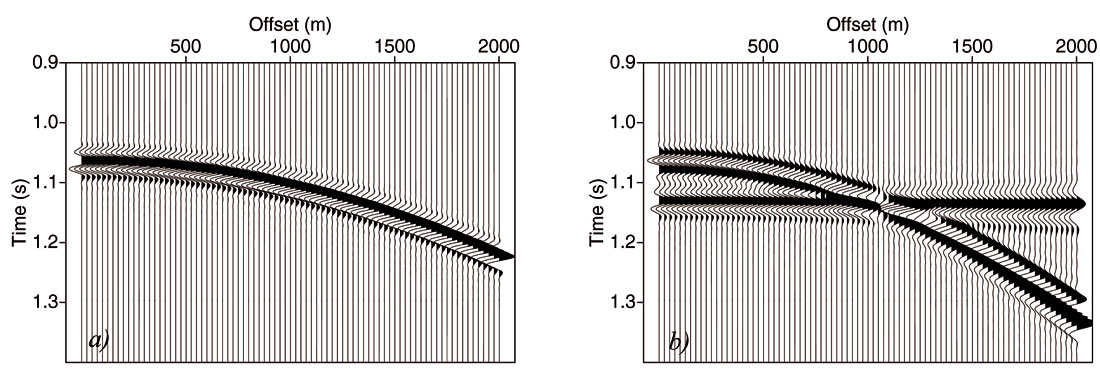
If we assume that our seismic data consists of only one event with a perfect parabolic (differential) move-out, such as displayed in Figure 1a, then we would expect only one spike in the parabolic Radon space, at the apex time and curvature of this event. However, when applying the forward transform as described in equation (1) we get a serious smearing in the Radon space, as visible in Figure 2a. This is due to the fact that the input data has limited offsets, generating artefacts in Radon space (see Kabir and Marfurt, 1999; Maeland 2003). Furthermore, when directly applying equation (2) to reconstruct the input, the expected input data is not obtained (Figure 2d). Apparently, this transform pair has to be modified to ensure a reconstruction of the input data in order to make this useful for multiple removal. One can conclude that the problems arise from the forward transform. Hampson (1986) suggested to replace the forward transform by a least-squares inverse of the backward transform. Actually, by doing this, the following inverse problem is solved: which distribution of data in the parabolic Radon space recreates the input data correctly. There are many solutions to this problem, i.e. many distributions in the Radon space will reconstruct the input data. The least-squares approach of Hampson (1986) will give that solution that has the minimum energy in the Radon space. Figure 2b shows this solution for the problem at hand, and Figure 2e shows the reconstructed input. Note that the artefacts have been reduced and – very importantly – that the original data has been properly reconstructed.

Still, the focusing in the Radon space is not optimal. Therefore, a so-called high-resolution version of the Radon transform was proposed by e.g. Thorson and Claerbout (1985) and Sacchi and Ulrych (1995). They proposed to use another constraint in Radon space, which solves the following problem: find the sparsest Radon space representation that still explains the input data. One disadvantage is that such sparseness constraint makes the Radon transform a non-linear optimization process, which is very computation intensive. However, the results are excellent, such as visible in Figure 2c, showing the high-resolution Radon domain of the parabolic event: the event maps onto one curvature parameter. Figure 2f shows a perfect reconstruction of the input event.

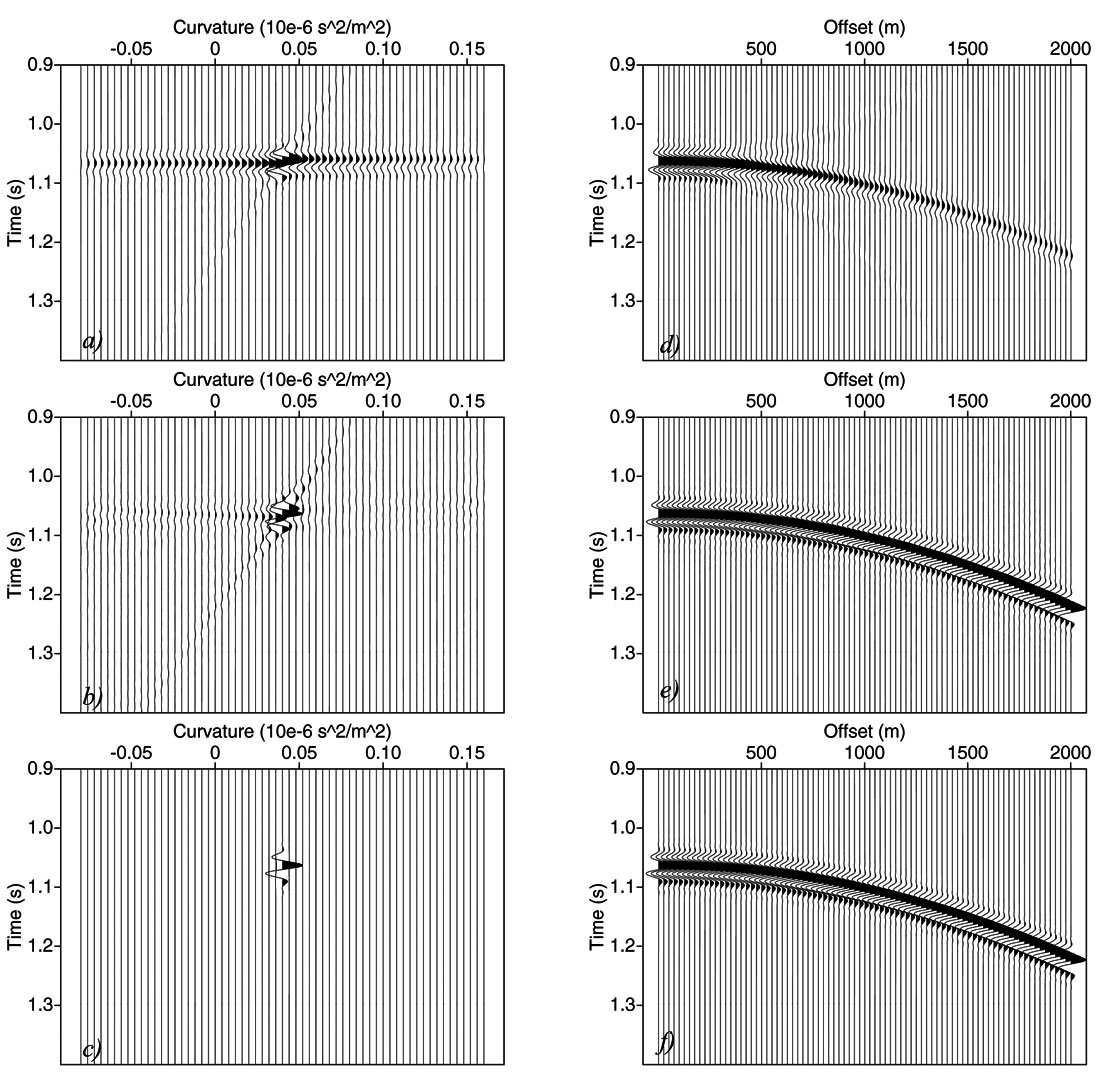
Herrmann et al. (2000) showed some impressive results of the use of a high-resolution implementation of parabolic Radon transform for removing multiples in field data. Thus, one might conclude that all problems are solved now: the high-resolution Radon transform will give an excellent focusing in the Radon space and also provides perfect reconstruction. However, this will only be the case if (1) the signal has a perfect parabolic move-out and (2) the wavelet is exactly the same for all offsets and (3) if the AVO is constant. In reality this is never the case. For example, AVO effects on the input data will give varying amplitude and phase along the event, NMO correction will introduce stretch effects, which results in a wavelet variation along the offset, the residual move-out will never be a perfect parabola, especially not when the subsurface has lateral variations (see e.g. Verschuur, 2006). All these effects result in a smearing of the event in the parabolic Radon domain. With other words: for non-perfect constant amplitude events with non-perfect parabolic move-out, we need more parameters in the Radon space to describe one event. You might say that the event becomes “broad-band” in the Radon space.

To demonstrate this, Figure 1b represents a more realistic seismic gather, which is in this case a true NMO-corrected primary and interfering multiple event, obtained from modeling in a horizontally layered medium. The amplitude varies with offset and also stretch effects are visible. Figure 3a shows the least-squares Radon transform of this data. It is clear that the deviation from a perfect constant-amplitude parabola gives additional smearing in Radon space. When muting the multiple and inverse transforming the muted result, Figure 3b is obtained. As this is synthetic data, the difference with the true primary can be calculated, which is shown in Figure 3c. Note that the primary is not fully reconstructed and, furthermore, part of the multiple is also visible, especially at the near offsets. If the multiple would be on top of the primary, this would give an additional amplitude distortion of the AVO from the primary. This observation has been reported by Kabir and Marfurt (1999) and they have illustrated this with many examples.

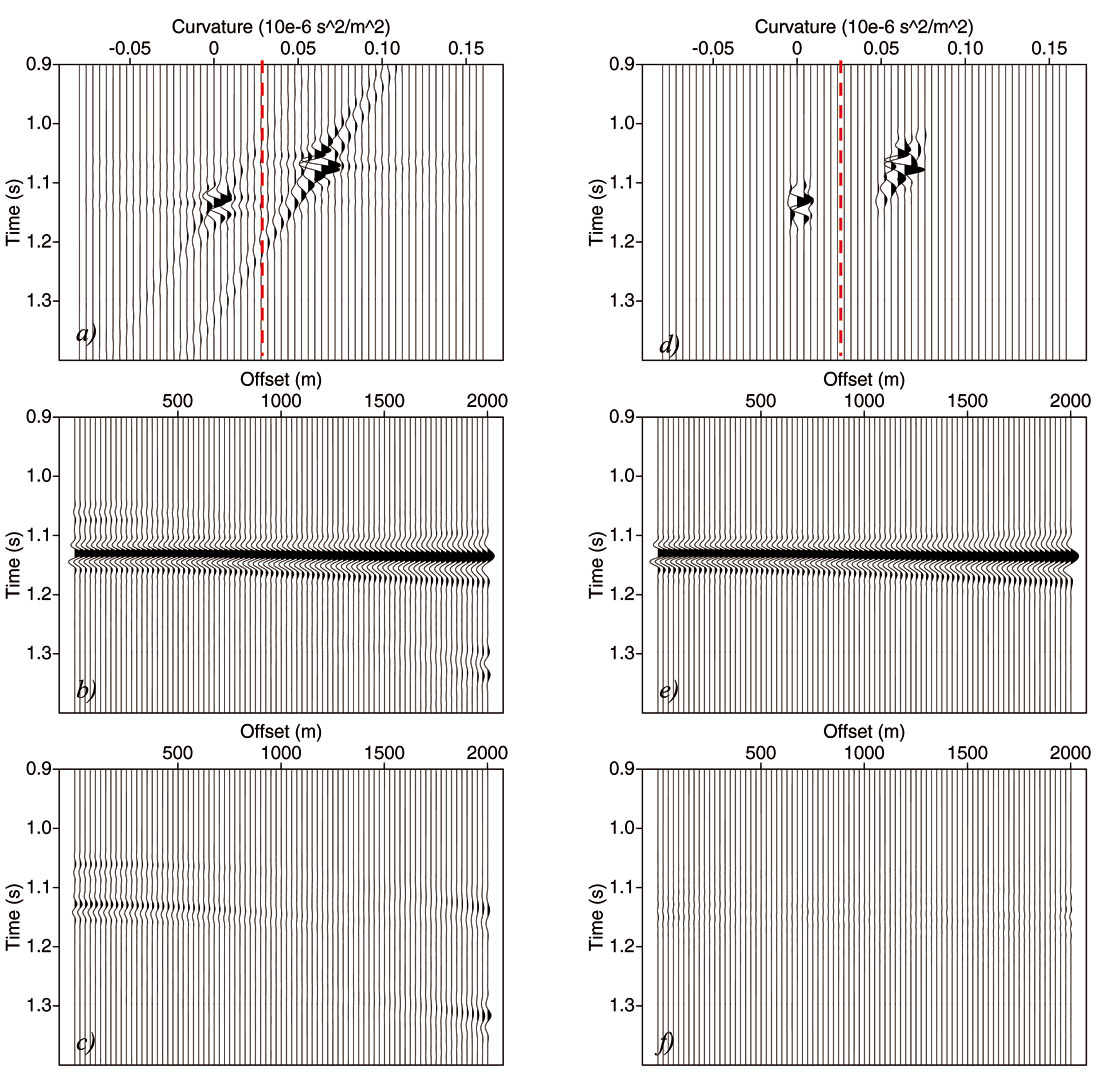
If the high-resolution Radon transform is used, the transform domain is given in Figure 3d, the reconstructed primary after muting in the Radon domain is plotted in Figure 3e and the difference with the true primary is depicted in Figure 3f. Note the improved separation in the Radon space, resulting in a reduced amplitude distortion in the reconstructed primary. However, note the fact that in the high-resolution parabolic Radon space there is smearing of the events, meaning that each event occupies a certain area in Radon space, because of the deviations from the perfect parabolas in the input space. Therefore, there is a principle limitation of primary/multiple separation in the parabolic Radon space, based on the shape and AVO of the seismic events. This means that if this smearing effect is larger than the separation between primaries and multiples, artefacts will occur in the estimated primaries, which can distort the AVO.

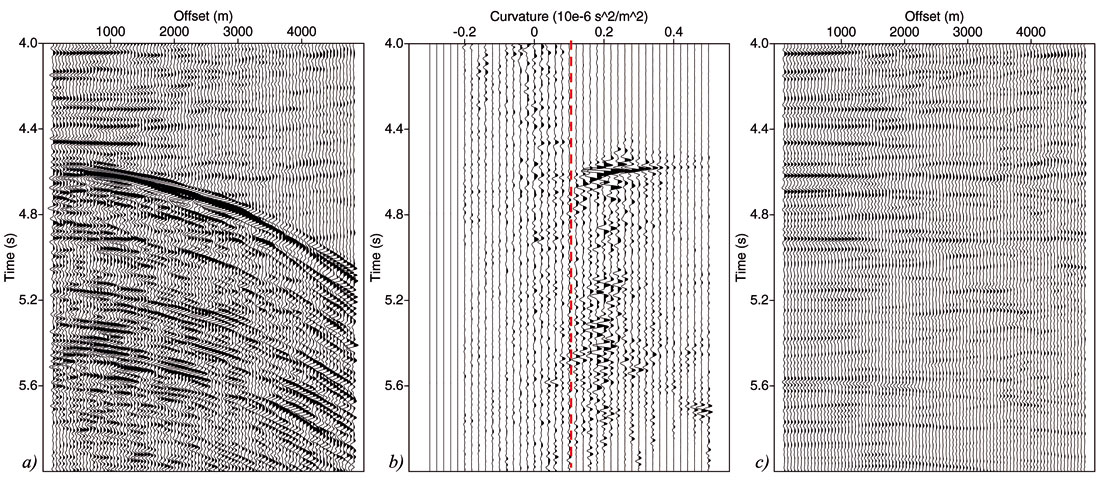
To illustrate this, we consider a CMP gather from a deep-water field dataset after NMO correction, as shown in Figure 4a. Primaries are more or less aligned and strong multiples are visible with residual move-out. However, it is also clear that the multiples are not constant amplitude, perfectly parabolic events.

It can be observed in Figure 4b, showing the L.S. parabolic Radon transform, that multiples and primaries overlap in Radon space. After muting the multiples along the red dashed line, and applying an inverse Radon transform, an estimate of the primaries is obtained. Especially around the near offsets there is residual multiple energy visible, which will have a serious imprint on the primary AVO. Furthermore, it appears that the AVO of the primary events exhibits some lateral smearing.

The use of the high-resolution Radon transform gives an improvement to this example, however, the smearing in Radon space cannot be removed and overlap between multiples and primaries will exist. The leakage around the near offsets, however, is greatly reduced due to the high-resolution Radon transform, but the reliability of the reconstructed primary amplitudes is still questionable.

Conclusions

In general it can be stated that multiple removal via the parabolic Radon domain can deliver quite good results. However, we should not expect miracles, as the application of such a tool means continuously making compromises. It will work at its best in areas with a reasonable simple geology without strong lateral velocity and structural variations, as this will ensure that residual move-outs of the multiples can be approximated with parabolas. Furthermore, the use of a high-resolution version of the parabolic Radon transform increases the separation between primaries and multiples and is therefore advised. Although not addressed in the above, the high-resolution version of parabolic Radon transform is also better capable of handling spatial aliasing effects. However, it is hard to completely avoid crosstalk between primaries and multiples, as AVO on the events and non-parabolic residual move-outs will give an inherent smearing of energy in the Radon domain. Thus, applying a mute in Radon space and inverse transforming the muted result can damage the AVO of the primary events.

D.J. Verschuur
Delft University of Technology