Why is it that volume interpretation of 3D seismic data is not practiced by seismic interpreters, though 3D seismic data is used by most oil companies for getting detailed information for the reservoirs? This is one question that most geophysicists at time wonder about. We decided to feature this question for our Expert Answers column, this month.
The Experts answering the question are Terry Zwicker (Samson Canada Ltd., Calgary), Ken Mitchell (K A Projects Ltd., Calgary), Doug Pruden (Nose Creek Geophysical Inc., Calgary), and Barrie Jose (Sproule Associates Ltd., Calgary).
The order of the responses given below is the order in which we received them. We thank the experts for sending in their responses.
Question
AVO in structured areas: Zoeppritz equations assume a plane wave source and a plane boundary. Yet we try and attempt AVO analysis in areas with varying degrees of structural complexities, by employing corrections to prestack seismic data for dip via DMO, pre-stack migration, etc. Do you think this is reasonable? What are the sources that may allow errors to creep into our analysis and what do you think still needs to be done in this area to get accurate results?
Answer 1
The objective of an AVO analysis is to produce accurate elastic rock property estimates in depth. In order to accomplish this objective, migration should play an important role. In dipping structure there is a complicated relationship between offset and angle that can only be resolved properly in the depth domain using subsurface angles. To achieve this ideal output, we should acquire the wavefield with sufficient spatial sampling so that migration can properly image all dips at all frequencies after the migration. On land, this is usually considered to be a cost-prohibitive solution, so compromises are made in acquisition and we try to compensate for them in processing to generate accurate elastic rock properties. Compromises made in acquisition result in surveys that are undersampled spatially, and this is particularly true for wide-azimuth land data. Such surveys cannot be used to measure high frequencies at high dips. In addition, the sparse sampling introduces migration noise through the inability of the sparse data to destructively interfere.
Nevertheless, Mosher et al (1996) clearly show the advantage of using pre-stack time migration (PSTM) before AVO. They demonstrate that AVO responses can be much better defined and more consistent with well control after migration than on unmigrated data. Tygel et al (1999) provide a mechanism to extend the methodology to prestack depth migration and from AVO to AVA (Amplitude Versus Angle) where the angles are more accurately determined as part of the migration process. In particular, Tygel examines the idealized situation of a well-sampled model and shows that the AVO response in the CMP gathers may not be as expected and that problems in the AVO response may not necessarily occur where one might expect them to be.
Common best practice, at least in marine AVO – where spatial sampling is less of a problem – is to run PSTM to offset or angle gathers and then run AVO analysis on these gathers. On land, the advent of azimuthal AVO for fracture detection is pushing us into more complex stratigraphy. This is because the fractures tend to occur where the rocks are bent the most; and when the rocks are bent, we need to use migration to image them properly.
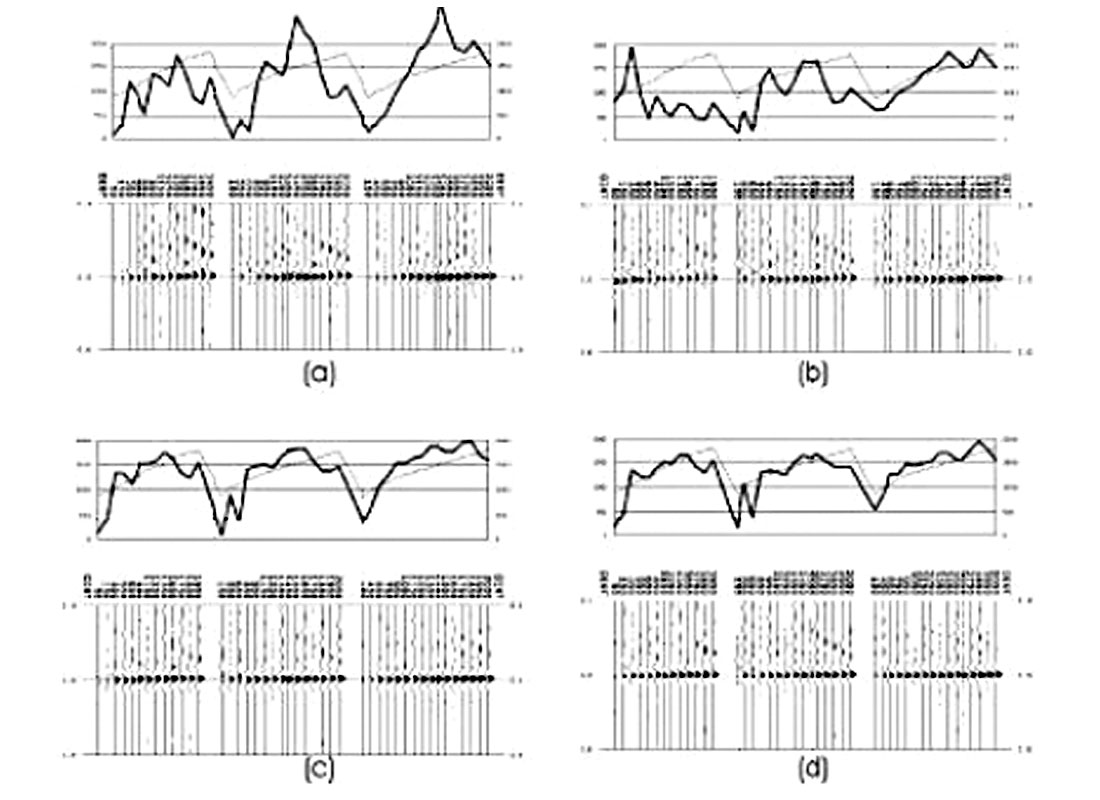
We need to continue improving the treatment of sampling before we can completely trust migrated amplitudes. A variety of solutions have addressed the problem of limitations in acquisition. These all amount to applying some sort of amplitude compensation that accounts for the spatially under-sampled data, such as hit-count weighting. We feel that the most successful of these methods to date is area-weighting (Zheng et al, 2001). Figure 1 shows the effects of various prestack migration weighting methods on the AVO response. The best of these is area-weighting in Figure 1d. We are also beginning to use pre-stack interpolation to generate better-sampled data. So far, this approach is applicable only in areas of moderate structure, and more work needs to be done to address where and how interpolation is applicable in areas of complex structure.
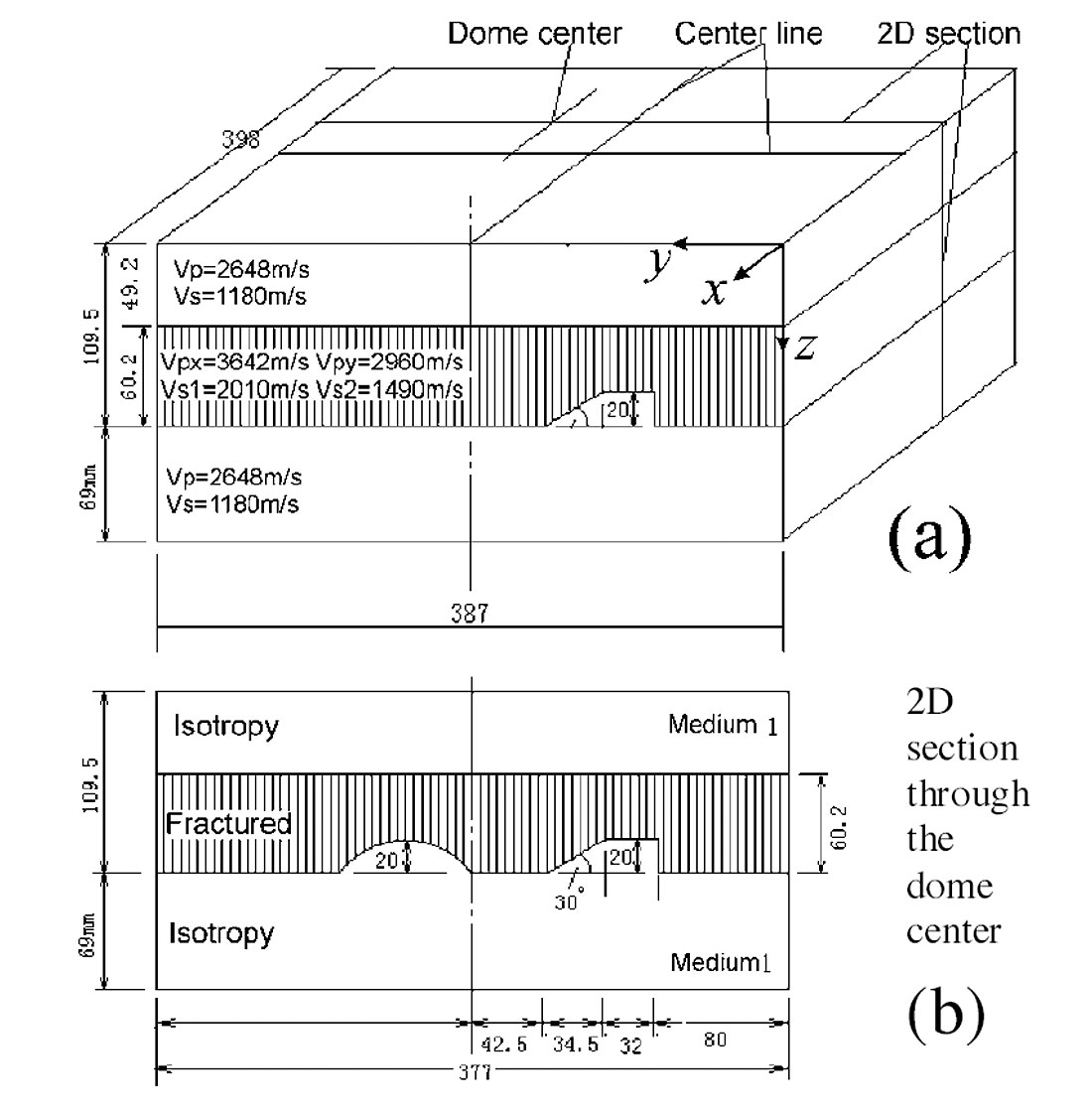
An area of recent attention is the variation of amplitude with azimuth. This variation is an indicator of the presence of anisotropy, which is frequently associated with vertical fracturing. Zheng and Wang (2005) examine the use of PSTM to estimate azimuthal AVO (AVAZ) from a physical model dataset. Figures from their paper are reproduced below. The model is an anisotropic medium sandwiched between two isotropic layers. The anisotropic layer has a ramp and a dome carved into its base to simulate a thrust and a reef, respectively. The ramp has a 30o dip and the dome has variable dips with shallow dips at the top and steeper dips on its flanks (Figure 2). The model is submerged and a wide azimuth survey was shot over it (Wang and Li, 2003). The model allows examination of the effects of both dip and curvature on the AVAZ response. Zheng and Wang show that using CMP gathers to estimate AVAZ response works well for the flat top of the anisotropic zone, but the structures at its base a re poorly imaged (Figure 3). However, PSTM after are a weighting allows for accurate measurement of the AVAZ response at least for the smaller dips. From this preliminary work, it appears that the PSTM is unable to recover the amplitude completely on the 30° dip on the ramp. Examination of the dome, which has variable dips, indicates that this PSTM method does a decent job of recovering amplitudes up to about 20°.
Early practitioners of AVO analysis sometimes used post-stack time migration of AVO attributes in areas where structure made it difficult to position these anomalies accurately. This was a tentative step in the right direction, and it had some success in moving AVO attributes closer to their correct location and collapsing the Fresnel zone. When using this method, the AVO anomalies generally appear to collapse and move updip, as one would expect from a post-stack migration. It would be unwise to drill on the edges of such features, but in areas of not-too-complex structure the middle of a large feature might be representative of the real AVO response. AVO and migration are not commutative, so from a theoretical standpoint, migrating AVO attributes should not be done. Ultimately, the only way to be sure of the result is to use migration before doing the AVO analysis. Additionally, it is very hard to get the flat gathers required by most AVO programs without using PSTM if there is too much structure. However, in practice, post-stack migration of AVO attributes seems to have been done successfully fairly often in areas where mildly dipping reflectors make it difficult to determine the position of AVO anomalies.
A likely candidate for future work on AVO and migration is Least-Squares Migration (LSM - Ronen and Liner, 2000). LSM is currently being examined for the purpose of addressing illumination issues, which also adversely affect AVO analysis, since poor illumination means that only a limited number of angles are available for AVO analysis. Currently, research is being undertaken to introduce AVO into LSM (e.g. Feng and Sacchi, 2004).
In conclusion, the best method currently available for AVO processing in moderately complex structure is to run pre-stack time migration on data processed following a true-amplitude flow and corrected for poor sampling by a method such as area-weighting. These migrated gathers are generally sufficiently accurate for AVO analysis. The practitioner is cautioned always to ensure that the AVO results are consistent with other information available on the prospect and to examine the pre-stack data (in this case, the PSTM gathers) prior to committing to drilling a well on any AVO anomaly.
David Gray, Sam Gray, Tianfei Zhu, Jonathon Downton,
Scott Cheadle, Richard Bale, Xiaogui Miao,Ye Zheng,
Veritas
Answer 2
When focusing on the details of a particular amplitude (AVO) anomaly, we sometimes overlook or ignore the complexities of the overburden, because of our preoccupation with the details of the elastic rock properties at the prospect level.
But performing quantitative AVO analysis and interpretation in areas of structural complexity, moreover requires a detailed understanding of the overburden and its affects on wave propagation. Then, appropriate processing techniques/workflows, and prestack imaging technologies can be brought to bare to produce more accurate image gathers for better AVO inversion, analysis and interpretation.
As the Zoeppritz equations are formulated over angle, central to this theme is the mechanism by which offset gathers are transformed to angle gathers. Methods that are based on refracted ray tracing schemes provide much better angle approximations than those relying upon simple straight ray assumptions. The use of the latter should therefore be avoided in areas of complex structure.
Continual improvement of 3-D prestack time (and depth) migration algorithms, combined with their now widespread use amongst geophysical service contractors, has resulted in a natural progression towards applying AVO analysis in more structurally challenging areas. However, while many of the prestack migration algorithms provide increasingly accurate structural images, they each have their shortcomings when it comes to AVO/ AVA analysis.
Ray-Based (Kirchhoff) Migrations
In areas where strong vertical, and moderate lateral velocity gradients persist, curved-ray prestack time migration is usually appropriate. Where both strong vertical and lateral velocity gradients exist, prestack depth migration is most likely necessary for accurate imaging, and subsequent AVO analysis.
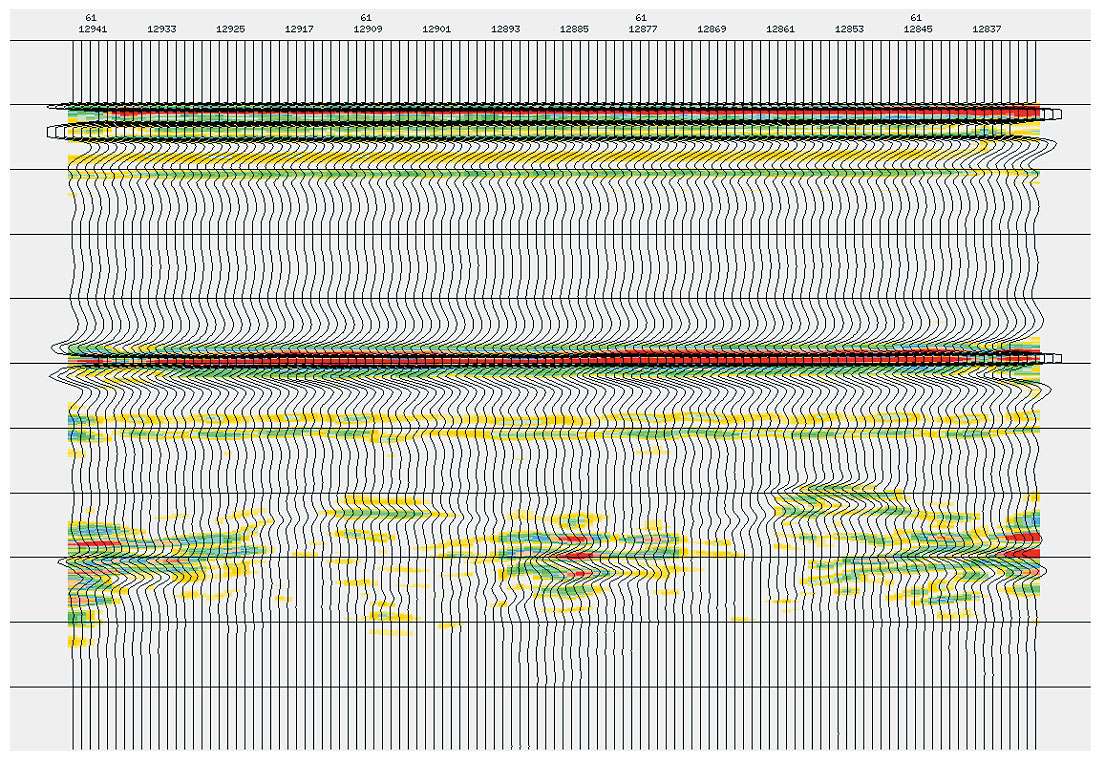
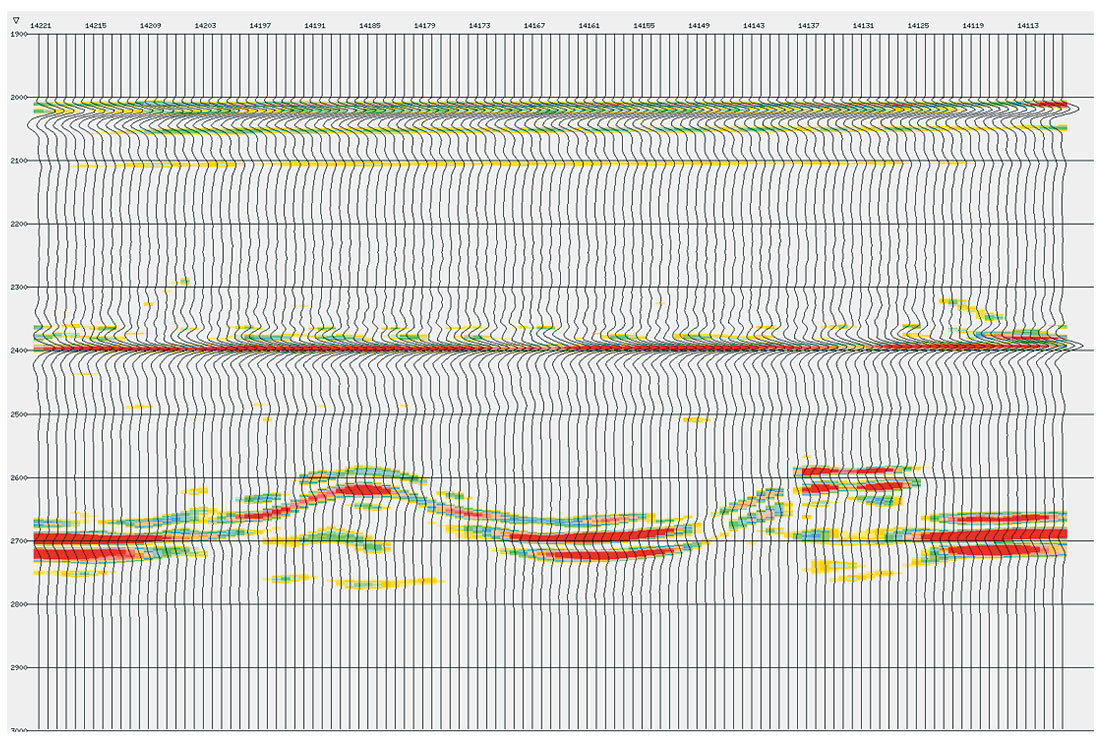
But prestack Kirchhoff migration is particularly susceptible to very significant amplitude distortions when acquisition geometries (azimuth and offset) are highly irregular. This can readily be seen in image gathers from Kirchhoff PSTM/PSDM, where higher input trace densities in the middle-offset ranges, result in much “hotter” mid-offset amplitudes, compared with those at the near and far offsets (Figure 1a.). All to often, angle range stacks and AVO attribute volumes are generated from image gathers with these distorted amplitudes. Clearly, their usefulness for fluid and/or lithology discrimination are severely limited.
Fortunately, several procedures can be incorporated into Kirchhoff prestack migration to minimize the effects of acquisition footprint. These procedures are described below, and example results presented in Figures 1a, 1b and 1c.
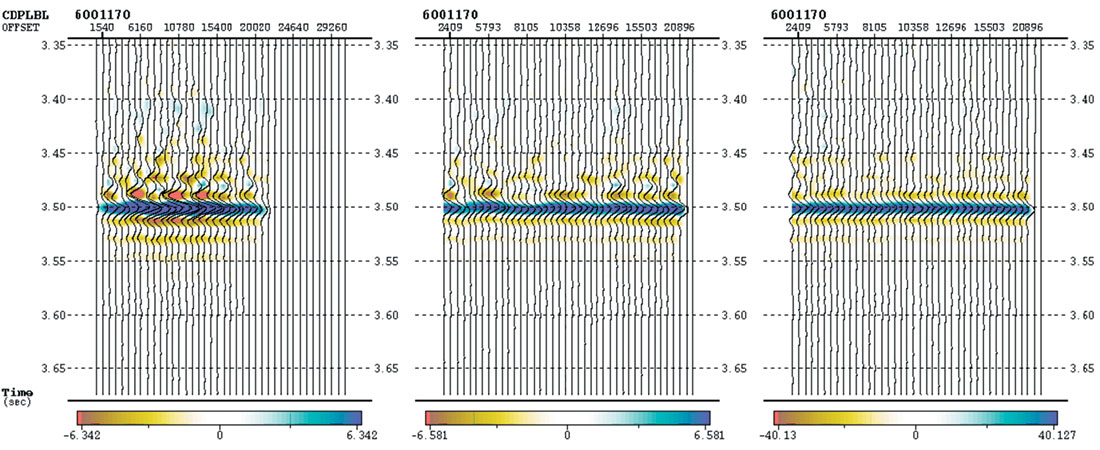
Figure 1b. PSTM gather with Regular Trace Distribution & No Geometry Weighting
Figure 1c. PSTM gather with both Regular Trace Distribution & Geometry Weighting
Trace Offset Equalization
Usually migrated gather offset increments are set to equal distances. But this can result in a significant variation in the number of input traces going into each offset bin. However, by varying the offset increments, such that the number of input traces in each output offset bin are the same, then a much better balanced AVO response is achieved (Figure 1b).
Geometry Weighting
Amplitudes scalars based upon input trace density can also be utilized in conjunction with “trace offset equalization” to further minimize the effects of irregular acquisition geometry (Figure 1c). These so-called “geometry weighting” schemes rely upon the construction of nearest neighbor polygons (Voroni diagrams) around each input trace, then apply a single trace amplitude scalar proportional to the relative area of the polygon that each trace occupies (Canning and Gardner, 1998). Not only do they minimize migration artifacts, they also result in much better balanced amplitudes with offset/ angle. However, geometry weighting should be applied with caution in areas or poor S/N. Also, time variant amplitude weighting may be appropriate for deeper prospects, due to increased trace mixing with depth.
Wave-Equation Migrations
In areas of severe structural (velocity) complexity, with associated multipathing of reflected energy, Kirchhoff depth migration methods often fail to image the subsurface correctly. Wave-equation based imaging methods have been shown to produce superior images under such conditions. Prucha et al. (1999) describe the use of wave-equation migration to generate angle-domain common image gathers for AVA (amplitude versus angle) analysis, as well as velocity analysis and update. But in practical computing terms, extraction of angle-domain common image gathers is expensive, and as a result the use of wave-equation migration for AVA analysis, at least to date, remains limited.
Velocities and AVO
It is well documented that AVO inversion, performed most commonly on a sample by sample basis, is very susceptible to residual move-out (RNMO) errors. It is usually necessary therefore, to undertake residual velocity analysis prior AVO to inversion, and extreme caution (viz. careful parameterization), where class I and class II AVO’s are the exploration objectives.
If large-angle offset ranges are required for AVO anomaly discrimination (for example, AVO class I), then higher order moveout terms may be necessary to correct for the so called anisotropy effect.
Any automated velocity analysis procedures, like AVO, are adversely affected by noise. Careful gather preconditioning and noise suppression should be performed prior to running any automated velocity picking. If gathers are close to flat prior to automatic velocity analysis (through careful imaging velocity analysis), then tighter (delta velocity) constraints can be used, and more stable results obtained.
Finally, to the Rock Physics
And finally let us not forget that the fundamental “building blocks” to any AVO analysis is in the underlying rock physics.
Building reliable elastic forward model(s) early on in the AVO workflow is critical not only to unraveling the relationship of AVO response to changing reservoir properties, but also in understanding the necessary steps that may be required during processing and imaging to produce gathers that are suitable for AVO analysis.
It is here that the disciplines of petrophysics/rock physics, processing/imaging and amplitude interpretation must be united, such that the challenge of applying AVO in structurally complex areas be met head on.
Jack Taylor
TRICON Geophysics Inc. Houston,TX











Share This Column