Tributes to Professor Tad Ulrych

On August 19, 2014, we learned of the passing of a great Canadian geophysicist, Professor Tad Ulrych. Tad had an illustrious and successful career at the University of British Columbia for more than four decades. He was a wonderful mentor, teacher and research scientist. In 2014, Tad received the CSEG Medal, the most prestigious award presented by the Canadian Society of Exploration Geophysicists*. Tad was a great friend and colleague to many of us and he will be deeply missed.

In this issue of the CSEG RECORDER, we present tribute articles written by four of Professor Ulrych’s former students: Larry Lines, Al Woodbury, Changjun Zhang, and Scott Leaney.

*2013 CSEG Medal Citation: See May 2014 RECORDER, page 42. csegrecorder.com/assets/digital/2014-05/#44
CSEG MEDAL presentation photo in May 2014: csegrecorder.com/assets/digital/2014-06/#77

Remembering Tad Ulrych
August 9, 1935 – August 19, 2014

Larry Lines, Introduction and Coordinator
Department of Geoscience, University of Calgary, Canada

As one delves into the life journeys of geophysicists, one finds that there are individuals who leave a lasting and unforgettable impression while impacting the direction of these journeys. For many who studied at UBC, Tad Ulrych was such an individual. My first impression of Tad was at the UBC campus in May 1972. I was completing my M.Sc. at the University of Alberta and was invited to visit the Department of Geophysics and Astronomy and to consider doing a Ph.D. in that Department. I had read Tad’s famous 1971 Geophysics paper, “Application of homomorphic deconvolution to seismology” and was very interested in his research. It was a beautiful spring day in Vancouver in 1972 and the geophysics department was in a relaxed and enjoyable mood when I first met Tad. My appointment with Professor Ulrych was slightly delayed since he had suffered from sunburn while skiing in the coastal mountains. In our initial conversation, Tad had a quizzical look on his face with a question.

“Lines, didn’t you once turn us down for your M.Sc. studies?” When I answered that I had done so due to some funding situation, Tad replied while waving in a dismissive manner (with a smile on his face): “Forget it”.

He then directed me to his office, whereupon we discussed his recent research. Tad instructed me to submit my application for the Ph.D. program and to come to UBC when I had completed my M.Sc. at the U of A. Tad struck me as a person with a warm engaging sense of humour that nicely complemented his intelligence and incisive insight into scientific problems.

Deconvolution days at UBC

Those years at UBC were exciting times in the development of seismic time series applications in deconvolution and spectral analysis. Soon after arriving in January 1973, I took Tad’s graduate class on spectral analysis. The class was filled with graduate students and postdoctoral fellows – many of whom were interested in Tad’s latest papers on maximum entropy. Tad was a superb lecturer. His lucid explanations about geophysical topics were outstanding. His enthusiasm infected both his students and colleagues alike.

Later that autumn, Ralph Wiggins (inventor of minimum entropy deconvolution) arrived from Toronto to join the faculty, along with a new M.Sc. student, Rob Clayton. Rob would later join Jon Claerbout’s Stanford Exploration Project and then become a professor at the California Institute of Technology. The discussions and collaborations among us occurred in the department’s coffee room and library, and the UBC computer centre. We were eager to compare these recent developments in homomorphic deconvolution and maximum entropy methods (MEM) to the classical approaches of Wiener deconvolution, as found in the papers of Robinson and Treitel (a summary of which was published in their 1980 textbook.)

Tad had described inversion, and deconvolution in particular, as a problem in which we had an equation of A + B = C. In this problem, we know C and we wish to determine A and B. These solutions are of course nonunique, but statistical differences in A and B may help us to find useful information. To understand this in the seismic context, we consider the seismic trace convolutional model,

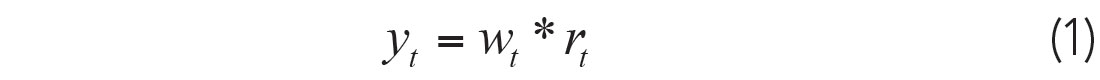
Here y_t is the seismic trace, w_t is the seismic source wavelet, and r_t is the desired reflectivity of a layered earth. We have recorded the seismic trace and wish to determine the wavelet and reflectivity.

If we Fourier transform equation (1), we obtain the expression for the Fourier transform of the trace as a product of Fourier Transforms.

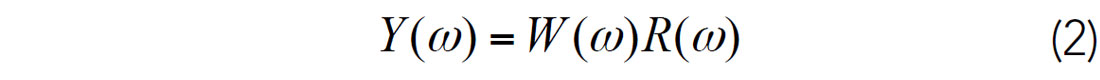
Therefore it would seem that we know the product of two numbers and wish to determine the numbers. If we take the logarithm of equation (2), we obtain:

In homomorphic deconvolution, we take the inverse Fourier transform of (3) and find ourselves in the cepstral domain. In this domain, we define the complex cepstrum as the inverse Fourier transform of the logarithm of the Fourier transform of a time sequence. In taking the inverse Fourier transform of (3), we obtain equation (4).

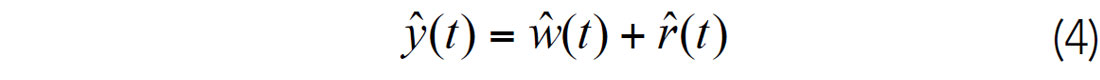
In this expression, the complex cepstrum of the seismic trace, , is equal to the sum of the complex cepstrum of wavelet and complex cepstrum of the . If the amplitude spectrum of the wavelet is smooth compared to the amplitude spectrum of the reflectivity in equation (2), then a “spectral analysis” would place at the low values of t in the cepstral domain – allowing for a separation of the wavelet cepstrum from the reflectivity cepstrum. The separation of the wavelet and reflectivity cepstrum would allow for a subsequent deconvolution. Equation (4) is exactly described by Tad’s description of A+B=C. We know C and we hope to determine A and B. Of course, this is a nonunique inverse problem that describes the problem of deconvolution. Nevertheless, we may know that A and B have statistical differences that allow us to separate them and provide useful solutions.

The Wiener deconvolution as described by Robinson and Treitel (1980) dealt with this inverse problem. In the case of Wiener deconvolution, we also assume different statistical differences between the wavelet and reflectivity. We simply state this in words, since the details are elegantly described in the papers of Robinson and Treitel. If we assume the reflectivity sequence, r_t , is random, the autocorrelation of the seismic trace, y_t , is equal to the autocorrelation of the wavelet, w_t (to within a scalar constant multiplier). Knowing the autocorrelation of the wavelet means that we can compute its power spectrum and subsequently its amplitude spectrum. Knowing its amplitude spectrum, we can then estimate the wavelet from knowledge of its phase spectrum. For impulsive seismic sources such as dynamite or air guns, we can assume a minimum delay in the energy of the source and compute a minimum phase spectrum. This allows us to compute the minimum phase wavelet, which can be deconvolved from the trace to produce a reflectivity sequence.

With both homomorphic deconvolution and Wiener deconvolution, certain statistical assumptions need to be made to perform deconvolution. Both methods could succeed – depending on the validity of the statistical nature of the wavelet or reflectivity. Our UBC research group held contests in wavelet estimation and deconvolution – first on synthetic models and then on real data. It turned out that while homomorphic deconvolution did well on data with good signal-tonoise, its demise came from phase unwrapping for noisy real data. In the latter situation, Wiener deconvolution appeared to be a more robust method. Subsequent papers on deconvolution from this UBC group appeared in many of the well-known geophysical journals.

Tad’s research on MEM, as expressed by Ulrych and Bishop (1975), showed new insights into spectral analysis through use of the Burg algorithm. The use of MEM also indicated possible generalizations of Wiener deconvolution through autoregressive models. Tad was always willing to think “out of the box” to find new methods of generalizing time series solutions.

A multidimensional academic life and mentorship

With Tad, life was much more than a one-dimensional academic existence in an office or lecture hall. Tad enjoyed ice hockey or soccer on the UBC campus, as well as skiing in the coastal mountains near Vancouver. One of the secrets to communicating with Tad was to participate in these sports and make an appointment following the game. Tad was one who enjoyed life to the fullest with the expectation that his students and colleagues should enjoy university life as well. His support of graduate students was unwavering – both financially and with intellectual input. Tad treated his graduate students much like colleagues rather than as subordinates. He encouraged independent thought and enthusiastically listened to input from students. There were many ongoing research discussions with his students in the class room, his office, the coffee room, or the local pubs. Tad was always approachable and generous – and never pretentious or aloof.

He was very supportive of his graduate students – both financially and with encouraging words. I remember when my first paper with Tad was rejected by Geophysics. This did not deter Tad from helping me to revise the paper and re-submit to another journal. This paper entitled “The old and the new in seismic deconvolution and wavelet estimation” was published in Geophysical Prospecting and later included in an SEG reprint book by Osman and Robinson (1996). Without Tad’s encouragement and persistence, our paper might never have seen publication.

There were so many ways that Dr. Ulrych mentored dozens of Ph.D. students at UBC for more than four decades. Tad was a mentor to me and a number of graduate students in subsequent generations, including Mauricio Sacchi (Head, Department of Physics, University of Alberta) and Kris Innanen (Director, CREWES, University of Calgary). Also, Tad was very well known in the geophysical research community, and introduced me to another great mentor, Sven Treitel, the leader of geophysical research at Amoco Production.

Inversion research on several continents

The time spent at UBC with Tad was certainly not the end of our collaborations. Following the Ph.D. defence and work at Amoco Canada, I went to Amoco Research Center in Tulsa to join Sven Treitel’s team in 1979. During the 1980’s, Tad Ulrych, Doug Oldenburg and Shlomo Levy started a company, Inverse Theory and Applications (ITA), and had Amoco as one of its clients. There were frequent communications with ITA and visits during SEG meetings. During this decade, Tad also collaborated with Bahia University in Brazil and visited with Toshi Matsuoka in Japan.

I remember that Tad and I were invited by Toshi to be keynote speakers in a tomography symposium at the University of Tokyo in 1990. It was a wonderful meeting that I will never forget – both scientifically and socially. A state-of-the-art tomography publication by Tamaki and Tamura (1990) was a result of the meeting. (People tell me that Tad and I were asked to stop singing so loudly in one of the Tokyo bars just before closing time at the end of the meeting.)

In the 1990’s, Tad returned to Canada from Brazil. I returned to Canada, first to Memorial University and then to the University of Calgary. Tad invited me back to UBC to give lectures on imaging and inversion. During these UBC visits, I was always impressed to see that Tad continued to attract many talented Ph.D. students including individuals such as Daniel Trad, Kris Innanen, and Scott Leaney. Tad’s magnetism and mentorship continued to be strong for at least four decades at UBC. During this time, Tad’s interests turned to Bayesian inversion and as SEG Editor of Geophysics, I remember receiving a number of lucid and interesting papers including a paper by Ulrych, Sacchi and Woodbury, entitled “A Bayes tour of inversion: A Tutorial” (2001).

A highlight of any trip to an SEG Annual Meeting was to meet with Tad and share a meal or a drink and compare notes on our latest adventures in research or travel. Tad was chosen to be SEG Distinguished Lecturer in 2008, and he travelled the world giving lectures on geophysical time series analysis. He seemed to have inexhaustible energy and enthusiasm.

Reflections on our last paper

In his late seventies, Tad’s health began to deteriorate. Yet despite physical handicaps, Tad’s mind was ever alert and his scientific productivity was continuously prolific. During the past five years, some of us became interested in seismic reflections due to contrasts in seismic-Q and a paper was published entitled Reflections on Q in the December 2008 issue of the CSEG RECORDER. The essence of the paper was based on the reflection coefficients for anelastic media. The reflection coefficient for P-waves impinging at normal incidence on a boundary is given by:

Where Z = ρv is the acoustical impedance of a layer. For elastic media, Z = ρv, the product of rock density and P-wave velocity. For anelastic media, the impedance becomes complex and is given by , as was recognized by White (1965) and later by Bourbie (1982). As a consequence of these generalized models of impedance, one could have reflections from contrasts in seismic-Q, even if there were no contrasts in the product of density * velocity. This was demonstrated in independent lab experiments by Carl Sondergeld and by Joe Wong. Tad did some calculations to validate these results. Together we published a paper in Geophysical Prospecting., entitled Experimental measurements of Q-contrast reflections. (Lines et al., 2014).

Celebration of a Wonderful Career

On September 5, 2013, Scott Leaney and others organized Tad-fest at UBC. Twenty-three geophysicists attended to celebrate Tad’s wonderful career with talks and toasts. Rob Kendall, the CSEG President, presented Tad with an award in recognition of his many accomplishments. Tad’s achievements were recognized by many awards including SEG Honorary Membership (2004), SEG Distinguished Lecturer (2008), and the CSEG Medal (2014), the highest award in the CSEG. While I personally was unable to attend Tad-fest due to a family medical situation, I was able to visit Tad in Vancouver on a one-day trip in June 2014. I was impressed by his long-term memory and enduring technical knowledge. He had many great questions, insights, and appreciation for the support of his daughter, Lyza. Tad Ulrych was a wonderful individual and an outstanding scientist who will be greatly missed. We can all appreciate his wide-ranging influence on those of us who shared some of his adventures in geophysics.

References

Bourbie, T., 1982, Effects of attenuation on reflections, Ph.D. thesis, Stanford University.

Lines, L.R., and Ulrych, T.J., 1977, The old and the new in seismic deconvolution and wavelet estimation, Geophysical Prospecting, 25, 512-540.

Lines, L., Vasheghani, F., and Treitel, S., 2008, Reflections on Q, CSEG RECORDER, December, 36-38.

Lines, L., Wong, J., Innanen, K., Vasheghani, F., Sondergeld, C., Treitel, S., and Ulrych, T., 2014, Research Note: Experimental measurements of Q-contrast reflections, Geophysical Prospecting, 62, 190-195.

Osman, O., and Robinson, E.A., 1996, Seismic source signature estimation and measurement, SEG Reprint Series, no. 18, Tulsa, OK.

Robinson and Treitel, 1980, Geophysical signal analysis, Prentice-Hall, Englewood Cliffs, N.J.

Tamaki, I., and Tamura, Y., 1991, Geotomography: Proceedings of the First SEGJ International Symposium on Geotomography, SEGJ Publication.

Ulrych, T.J., 1971, Application of homomorphic deconvolution to seismology, Geophysics, 36, 650-660.

Ulrych, T.J., and Bishop, T.N., 1975, Maximum entropy spectral analysis and autoregressive decomposition, Reviews of Geophysics and Space Physics, 13, 183-200.

Ulrych, T.J., Sacchi, M.D. and Woodbury, A., 2001, A Bayes tour of inversion, a tutorial, Geophysics, 66, 55-69.

White, J.E., 1965, Reflections from lossy media, The Journal of the Acoustical Society of America, 38, 604-607.

The legacy of Tadeusz J. Ulrych in hydrology; a journey towards maximum entropy

Allan D. Woodbury^†,
Professor Emeritus, Department of Civil Engineering, University of Manitoba, Canada

^†Visiting Professor, Earth & Environmental Sciences, University of British Columbia, Canada

With the death of Tad Ulrych, a truly great mind has passed from the living to the cherished memory of his family, friends and colleagues, and into history. His extensive scientific production, principally in time series and inverse problems²⁰, established him as one of the most influential geophysicists of our time. I know that Tad considered his “home” to be the SEG and its community of exploration geophysicists, and there he developed deep friendships and strong ties to industry.

But, to my consternation at least, he greatly downplayed his contributions in other areas of geophysics such as climate science³, and surface and subsurface hydrology¹⁷. Of all of his collaborators over the years only Mauricio Sacchi has coauthored more papers with Tad than me, and these are in the above mentioned areas of hydrology. Of course, this is not a contest and I only mention this in terms of his impact in geophysics which many reading this would not be aware of. Let me further detail these comments below. Note that only partial references to the published literature are given here.

The principle of maximum entropy (PME) originally developed in information theory and statistical mechanics by Jaynes in the 1950’s has had a wide range of applications in numerous fields2. A great variety of entropy applications in surface/subsurface hydrology and water resources have also been reported, and new applications are continuing to unfold^{1,18,21, 22, 23, 24}.

Reviews of the literature show that entropic measures can be used in the derivation of a number of typical frequency distributions used for hydrological analyses^{6,9, 21, 22, 23, 24}. Because hydrological characteristics can often be conceptualised as prior probabilities, these then can be incorporated in the distributions, yielding an approach that can be applied to areas having limited data. Entropy measures also yield a relatively simple and effective method of parameter estimation, which rivals that of Bayesian and maximum likelihood estimation². Since the PME can be applied to derive functional relationships between random variables^{16,17, 21, 22, 23, 24}, it has an advantage of performing multivariate stochastic analysis. Entropy fundamentally is a measure of the uncertainty of probability in a hydrological system, and is thus applicable to choosing between alternative models and in the design of hydrological networks for data collection.

The similarity between maximum entropy (MaxEnt) and minimum relative entropy (MRE) allowed for advances in information measures to obviate some of the shortcomings of the former method¹³. The advantages that MRE has over MaxEnt are that (1) the relative entropy measure is invariant under a coordinate transformation, (2) a prior probability is allowed, (3) non-positive models are supported, and (4) uncertainty in the model follows naturally and immediately. The purpose of the our research was to extend the theory and practise of MRE and empirical/hierarchical Bayes⁸, with particular reference to: (1) reconstruction of groundwater pollution source release histories from sampling groundwater concentrations^{7,12,13,14,15}, (2) the recovery of past ground surface temperature changes from temperature measurements taken in boreholes^5,11, (3) paleoclimate O₁₈ sources at the land surface inverted from observations in deep aquitards⁴, (4) hydraulic property inversion from aquifer models using empirical Bayes^5,10, and (5) improved parameter estimation from L-moment and C-moment data⁹. The MRE-based approaches have been extended to streamflow forecasting, and research is ongoing to extend them to drought forecasting.

Finally, I will detail what I see is the legacy in hydrology of Tad Ulrych’s work in entropic studies. One of the main problems plaguing both surface and subsurface hydrology in Canada is simply the lack of sufficient data^16,17. Frequently, either the data stream is of insufficient length, contains missing data points, or is inaccurate. More often than not, it is the data that seems to drive the model type and needs, and not the other way around. Furthermore, subjective information such as “rules of thumb”, professional experience, judgement, empirical rules, and so on have played a significant role in hydrological practice both here in North America and abroad. Conventional deterministic models do not have the capability to accommodate such subjective information (at least in a formal way) although the prior information may be totally adequate. The potential for applications of information-entropy theory is enormous in Canada and in developing countries, because it maximizes the use of information contained in data, and it permits the use of subjective information1. The PME when applied to these cases forces all observers who possess common information to produce consistent results. Furthermore, the PME, through what is called the “entropy concentration theorem”, offers an objective approach for drawing inferences as to the validity of modeling results¹³. Lastly, entropic modelling is effective and efficient, requiring relatively little computational effort, and is versatile in its applicability across many sub-disciplines within surface and sub-surface hydrology. Recent studies in hydrology^{21, 22, 23, 24} show that entropy can be used to: (1) derive surface infiltration relations from constraining moments¹, (2) model seepage and unsaturated flow¹⁹, (3) evaluate data acquisition systems including estimation of missing data, (4) assess the uncertainty in hydrologic models¹⁶, (5) water resources availability assessment²⁴, (6) sediment transport, (7) velocity distribution and open channel flow characteristics³, (8) environmental flows²³, (9) water distribution reliability²³, (10) ecological modeling²⁴, and a host of other topics.

The unique aspect of Ulrych’s inspired research is that it integrated detailed field observations of the temporal and spatial variability of hydrologic parameters with Bayesian/Maximum Entropy viewpoints of probabilities2 and high-resolution numerical simulations¹⁰. Research performed by Ulrych and collaborators in the last few decades has been highly successful and has led to a number of benchmark contributions^{8,10,12,15,17} in surface and subsurface hydrology, and has found, and continues to find, new applications in a variety of scientific and engineering problems.

Acknowledgements

Tad Ulrych left an outstanding legacy of teaching, research and mentorship, from which I greatly benefited. My sincere appreciation to Dr. Vijay Singh, who read over this comment and provided some very useful suggestions and other references to consider.

References

1. Woodbury, A.D., Comment on: Entropy theory for derivation of infiltration equations by V.P. Singh, (2010), Water Resources Research, 48, W08802, doi:10.1029/2012WR012322, 2012.
2. Woodbury, A.D., Minimum relative entropy, Bayes and Kapur, Geop. J. Int., doi: 10.1111/j.1365-246X.2011.04932.x, 2011
3. Ulrych, T.J. and A.D. Woodbury, An Occam’s razor view of the lead-lag dispute in global warming, The Leading Edge; August 2009; v. 28; no. 8; p. 914-917; DOI: 10.1190/1.3192838
4. Hendry, M.J. and A.D. Woodbury, Clay aquitards as archives of Holocene paleoclimate: 18O and Thermal Profiling, Ground Water, 45(6), 683-691, 2007.
5. Woodbury, A.D. and G.A.G. Ferguson, Ground surface paleotemperature reconstruction by information measures and empirical Bayes, Geop Res. Let. Vol 33, DOI:10.1029/2005GL025243, 2006
6. Woodbury, A.D., A FORTRAN program to produce minimum relative entropy distributions, Computers in Geosciences, 30, 131-138, 2004.
7. Ulrych, T. J. and A. D. Woodbury, Extension of minimum relative entropy for noisy data, Journal of Contaminant Hydrology, 67(1-4), 13-25, 2003.
8. Ulrych, T.J., Sacchi, M. and A.D. Woodbury, A Bayes tour of inversion: A tutorial, Geophysics, 66(1), 55-69, 2001.
9. Ulrych, T.J., Velis, D.R., and A.D. Woodbury, L-moments and C-moments, Stoch. Envir. Res & Risk Assess., 14(1), 50-68, 2000.
10. Woodbury, A.D., and T.J. Ulrych, A full-Bayesian approach to the groundwater inverse problem for steady state flow, Water Resources Research, 36(8), 2081-2093, 2000.
11. Kennedy, P.L., Woodbury, A.D. and K. Wang, Minimum relative entropy: theory and application to surface temperature reconstruction from borehole temperature measurements, Geop. Res. Letters, 27(19), 3081-3085, 2000.
12. Woodbury, A.D., Sudicky, E.A., Ulrych, T.J. and R. Ludwig, Three-dimensional plume source reconstruction using minimum relative entropy inversion, J. Cont. Hydrol., 32, 131-158, 1998.
13. Woodbury, A.D. and T.J. Ulrych, Minimum relative entropy and probabilistic inversion in groundwater hydrology, Stochastic Hydrology and Hydraulics, 12, 317- 358, 1998.
14. Woodbury, A. D., and T. J. Ulrych, Reply to: “Comment on: Minimum relative entropy inversion: Theory and application to recovering the release history of a groundwater contaminant by Kabala and Skaggs”, Water Resources Research, 34(8), 2081-2084, 1998.
15. Woodbury, A.D., and T.J. Ulrych , Minimum relative entropy inversion: Theory and application to the source release history of a groundwater contaminant, Water Resources Research, 32(9), 2671-2681, 1996.
16. Woodbury, A.D., F.W. Render and T.J. Ulrych, Practical probabilistic groundwater modeling, Groundwater, 33(4), 532-538, 1995.
17. Woodbury, A.D. and T. J. Ulrych, Minimum relative entropy: Forward probabilistic modeling, Water Resources Research, 29(8), 2847-2860, 1993.
18. Cui, H. and V.P. Singh, Configurational entropy theory for streamflow forecasting, J. Hydrology, 521,1-17,2015.
19. Singh, V.P., Entropy Theory for Movement of Moisture in Soils. Water Resources Research, Vol. 46, W03516, doi:10.1029/2009WR008288, pp. 1-12, 2010.
20. Ulrych, T.J. and M.D. Sacchi, Information-based Inversion and Processing with Applications, Handbook of Geophysical Exploration, Vol 36, 2005.
21. Singh, V.P. Hydrologic synthesis using entropy theory: Review, J, Hydrol. Eng. 16,421-433, 2011
22. Singh, V.P. Entropy Theory and its Application in Environmental and Water Engineering, John Wiley, 642 p., 2013.
23. Singh, V.P. Entropy Theory in Hydraulic Engineering: An Introduction. ASCE Press, 2014, 785 p.
24. Singh, V.P. Entropy Theory in Hydrologic Science and Engineering. McGraw-Hill Education, 824 p., 2015

Deblending OBN Seismic Data from Simultaneous Sources

Changjun Zhang, Seabed Geosolutions, USA

“One of Ulrych’s greatest passions probably was to solve for A and B in, A+B=C, when we only know C.” There are numerous signal estimation problems which can fit into this model. Separation of simultaneous source data is one among them. This task emerges when two or more source vessels are working at the same time in an ocean bottom node seismic survey project. The recorded data is C and signals from individual sources are A and B respectively. The research reported in this paper is one of my works enlightened by a great mind, Tadeusz J. Ulrych.

Introduction

In an ocean bottom node (OBN) seismic survey, nodes or receivers are often, if not always, sparsely distributed, mainly because of the tremendous workload to deploy and retrieve the nodes in the sub-sea environment. Also, a node survey is primarily conducted for a reservoir surveillance project, where wide or full azimuth and high fold observation is ideally expected for imaging under complex overburden, like gas clouds, salt bodies or basalt structures. Therefore, we need to shoot more sources than in other surveys to get good illumination of the sub-surfaces. In order to reduce the survey time, we have two options: one is shooting more frequently using a single source; another is simultaneous shooting using two or more source vessels. The efficiency of the first option is naturally limited by the required time to prepare the airguns and to sail the vessel to a pre-plot source position. Simultaneous source (SimSrc) shooting with two or more source vessels during an OBN survey can significantly increase operation productivity. However, the opportunity to improve the value versus cost ratio depends on the ability to process the blended data at an acceptable quality and on a short and predictable schedule.

Although some research has been done on blended data imaging without separation (Dai et al., 2011), separating SimSrc data into independent shot gathers, so that the data can be piped into a regular seismic data processing flow is still preferred now and in the foreseeable future. Deblending can be handled as a noise reduction problem to treat the interference from the other source as random noise (Huo et al., 2009, and Kim et al., 2009). It can also be handled in the framework of iterative signal estimation (Spitz et al., 2008, Abma et al., 2010 and Mahdad et al. 2011). The method introduced in this article follows the second paradigm. However, our method is developed based on the typical OBN acquisition geometry, and implemented in an individual node gather, where coherent energy in one source line is incoherent noise in the other source line. We use a local weighted tau-p transform to estimate the coherent energy. Through iteration, incoherent interference in two source lines gets attenuated alternately. Our method is much more light-weighted than methods handling data in the common offset domain or in other domains which require data sorting. The following details our idea using the case of two source simultaneous shooting, but theoretically, the methodology applies to an arbitrary number of simultaneous sources as well.

Methodology

OBN data are regularly processed in common node gathers. A continuous recorded data trace is mapped onto multiple traces of a given record length based on the actual shooting time of each source. For the example of two source vessels shooting two different lines, when using the shooting times from one source vessel for the mapping, energy from the other vessel will appear as interference noise.

Continuous data mapping

Ocean bottom autonomous nodes can record seismic data on the seabed continuously for months and the data can generally only be accessible after a node is retrieved. The continuous super long record on the entire disk needs to be mapped to a node gather before it can be further processed. The trace mapping simply takes a specified number of samples from the continuous record as an individual trace by matching the shooting time and the node internal clock time. For the case of two source vessel shooting along two sail lines, when using the shot times from one source vessel for the mapping, energy from the other vessel will appear as interference noise. The regularity of the shot interval may vary, but the interference is generally incoherent. Concisely, we denote the continuous recording as C, the signals from of one source vessel is A, and that from the other source vessel is B. The node recording contains energy from two sources, that is,

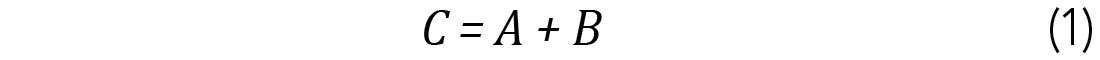
Using the shooting time of A to map this continuous trace, we will have an A gather, where A appears as normal energy, and B appears as interference, which is represented by β.

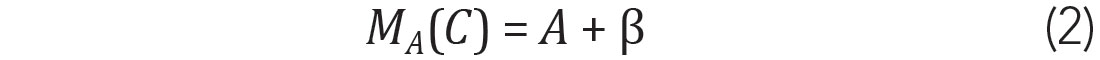
On the other hand, A will become interference in a B gather, and similarly, it is represented by α.

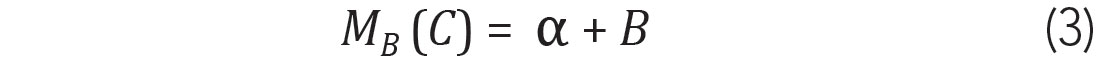
In equation (2) and (3), M_A and M_B represent two mapping operations and also the obtained gathers. The goal of simultaneous source data deblending is to separate A from B, when only C is known. In other words, we need to remove α from M_A. Incoherent interference is not random noise but randomly shifted traces. Compared with the coherent energy, their amplitude spectra are very close, but their phases are different.

Alternate Signal Estimation and Subtraction

Rather than treating α and β as random noise, the scheme of alternate signal estimation and subtraction works iteratively on two gathers. Estimating coherent energy from M_A, and subtracting this signal as noise α from M_B as noise β. Attenuated interference noise levels will contribute to more reliable signal estimation, and the iteration of estimation and subtraction converges. The success of the method relies on an efficient coherent energy estimation. Here, we choose to use a weighted tau-p transform (Zhang and Olofsson, 2012). The idea of weighted tau-p transform is simple. Conventionally, the tau-p transform is the summation along dips. In weighted tau-p transform, besides calculating the energy summation along dips, we also compute a coherence or similarity weight along the dips. Each sample along a dip has its own weight. Only the samples with a weight exceed a threshold and these samples are selected as representing coherent energy. There could be other coherent energy estimation methods that exist, and this weighted tau-p transform works very well for our case.

Preprocessing requirements

The first pre-processing step for data deblending is source de-signature. As is done in conventional marine streamer exploration, the far-field signature of the source array in an OBN survey can be recorded. An inverse filter is then deterministically designed and applied to the data. This source de-signature process shrinks a recorded wavelet which always contains the bubbling effect. A sharp wavelet is very helpful for coherent energy estimation. The second important pre-processing step is direct arrival alignment. This step could include several sub-steps, e.g. clock-drift correction, source position adjustment and water column velocity correction. The aim of these sub-steps is to assure the direct arrival from different source positions to the node is following a hyperbola, and correspondingly weak reflections and refractions appear as coherent energy. Although, these two processing steps are fundamental for OBN seismic data processing, they are best to be done before deblending to shrink seismic wavelets and to align the signals.

Data examples

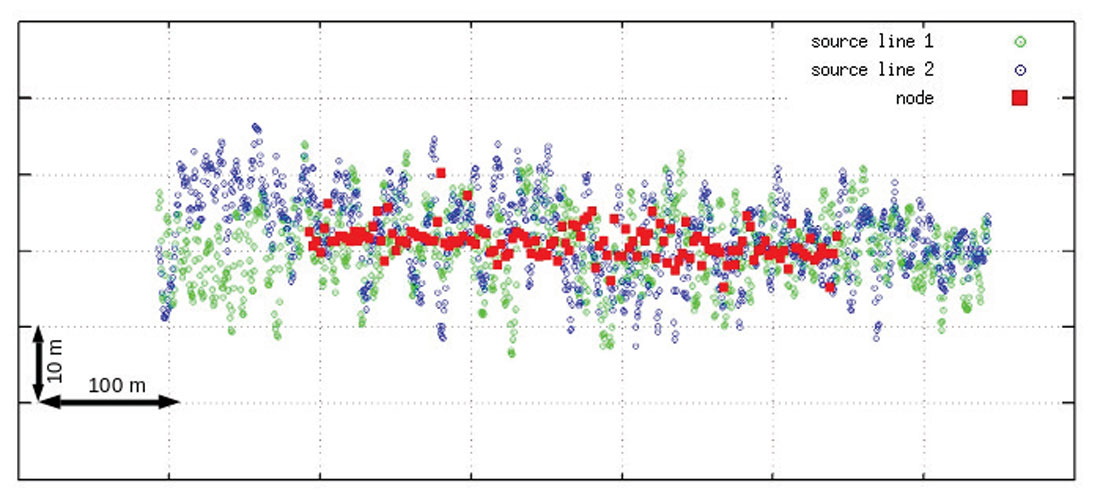
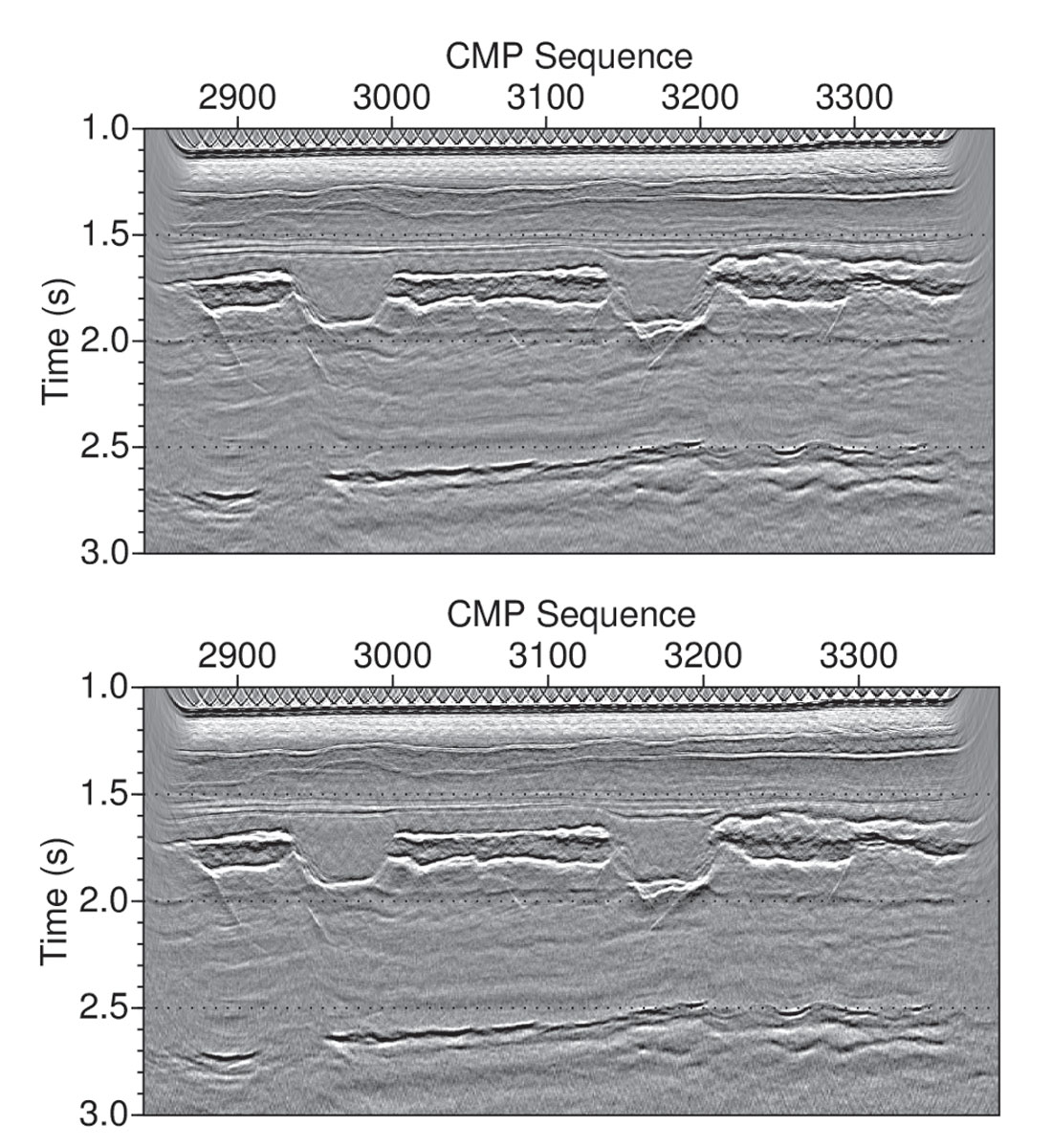
Because no real SimSrc data is available to show, we test our algorithm on a pseudo-blended dataset, which was created by mixing data from two real sail lines acquired by Seabed Geosolutions in the North Sea using relatively irregular shooting times. Shown in Figure 1 is its main-line acquisition geometry. The red squares represent the node positions. The green dots are source locations from one sail line; the blue dots are source positions from the other sail line. The source vessel sailed in one direction and turned back after reaching the end of the source line. Because of sequential shooting, in the original data, there is no cross-talk among source lines. To simulate SimSrc shooting, we modified the actual shooting times, i.e., let source vessel 1 travel along the green dots and source vessel 2 travel along the blue dots at the same time but in opposite directions. We created a simultaneous source dataset with two source lines. A pseudo-blended node gather selected from the simulated dataset is shown in Figure 2. The left half is the node gather of source line 1 and the right half is the gather of source line 2. Interference in the two gathers is present in the area approximately under a hyperbola with shifted apex relative to the coherent energy. The result after separation is shown in Figure 3, in which incoherent interference has been attenuated and the coherent energy is preserved.

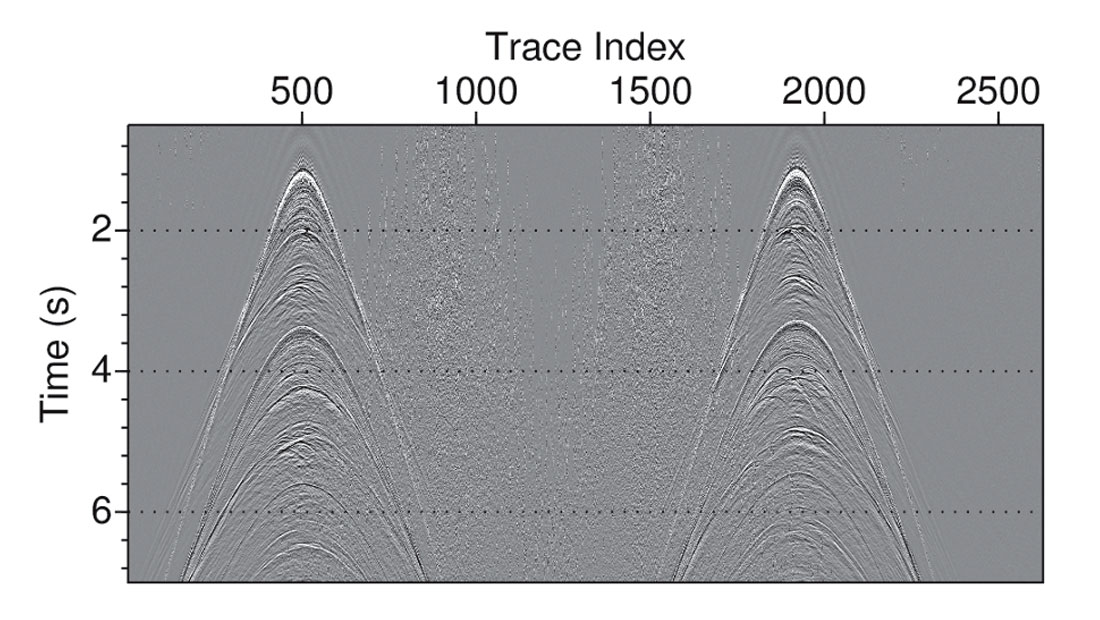
The post-stack migrated sections of the conventional data and the SimSrc data are shown in Figure 4. In (a) is the migrated section of original data, and in (b) is the migrated section of blended and then separated data. By comparing these two sections, we can see that the deblending processing keeps the reflections mostly untouched. This shows our methodology can separate the SimSrc data and does negligible harm to the reflections.

Conclusions

We introduce an iterative signal estimation methodology to deblend SimSrc data, which works alternately on receiver gathers from different source lines. The kernel of the algorithm is to extract coherent energy from one source line and subtract it as noise from the other source line. With attenuated interference, the algorithm will give better estimation of coherent energy with iterations. To estimate coherent energy, we use a weighted tau-p transform, which weighs down interference and protects coherent events. We detailed the scheme using a pseudo-OBN dataset acquired with two source vessels simultaneously, but the method also works for surveys acquired with more than two source vessels. With this method, and with increasing experience of processing blended data, we expect that simultaneous source shooting will provide a better value proposition than the current state of the art of sequential shooting.

References

Abma, R., Manning, T., Yu, J., Tanis, M., and Foster, M. [2010] Sparse Inversion of Simultaneous Sources: 72nd EAGE workshop on Develoments in Land Seismic Acquisition for Exploration.

Dai W., Wang, X., and Schuster, G. [2011] Least-squares migration of multisource data with a deblurring filter, Geophysics 76, R135-R146.

Huo, S., Y. Luo, and P. Kelamis, 2009, Simultaneous sources separation via multi-directional vector-median filter: SEG Technical Program Expanded Abstracts, 28, 31–35.

Kim, Y., Gruzinov, I., Guo, M. and Sen, S. [2009] Source separation of simultaneous source OBC data: 79th Annual International Meeting, SEG, Expanded Abstracts, 51-55.

Mahdad A., Doulgeris, P. and G. Blacquiere, G. [2011] Separation of blended data by iterative estimation and subtraction of blending interference noise: Geophysics, 76, 9-17

Spitz, S., Hampson, G. and Pica, A. [2008] Simultaneous source separation: A prediction subtraction approach: 78th Annual International Meeting, SEG, Expanded Abstracts, 2811-2814.

Zhang, C. and Olofsson, B. [2012] Separating Simultaneous Source Data Using Weighted Tau-P Transform: 74th EAGE Conference & Exhibition.

Tad Ulrych and me

Scott Leaney, Schlumberger, Houston

Through this article I would like to share some of my personal history with this great man, and take the opportunity to weave in an interesting bit of unpublished material from back in the day.

I met Tad in January of 1984 at UBC as a student taking his 514 course, “Time Series Analysis”. I enjoyed lectures from other great professors at UBC but none more than Tad’s, always infused with passion, insight and humor. In the last lecture he talked about attenuating reverberations in concert hall design and his love of music and that was it – I decided that I wanted him as my graduate supervisor.

Unfortunately Tad was leaving for Brazil for a year and could not fund me as an M.Sc. student, but thanks to the Canadian government I got the required funding and chose Tad as my supervisor in spite of his absence. While he was away I struggled with the problem of automatic well log correlation, the topic I had selected for my thesis.

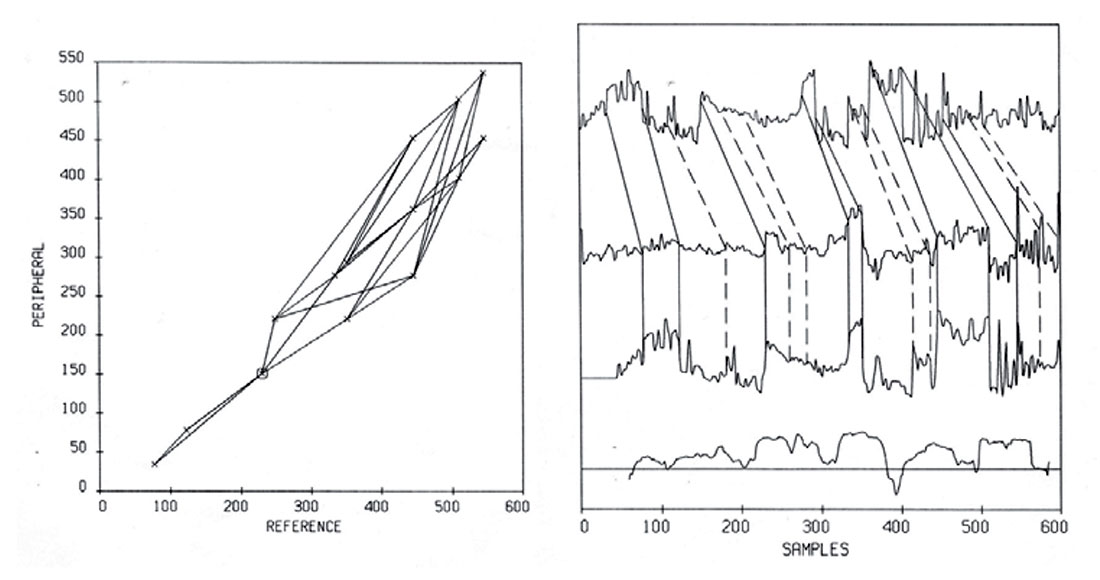
One of Tad’s grad students at the time and a good friend – Toshi Matsuoka – gave me a paper that would open a new direction for me – “Scale-space filtering” (Witkin, 1983). Toshi must have recognized that the problem I was working on was related to artificial intelligence and computer vision for robotics, a hot topic at the time. I feverishly coded up the ideas put forth in that famous paper and applied it to some sonic logs.

The idea of scale-space is that the most significant edges in a signal persist under increased filtering or the scale at which a signal is viewed. Witkin’s scale-space makes use of a Gaussian smoothing kernel and its derivatives. Zero crossings of the 2nd derivative correspond to edges, but such edges move laterally with increasing smoothing or scale, so to recover the original edge location edges must be tracked through scale. Figure 1 shows the results of such a process. The well log correlation technique that I ultimately developed operates by combinatorially associating edges from logs and optimizes a parsimonious similarity functional, continued from coarser to finer scales to produce the result shown in Figure 2. These results were generated after my MSc was already completed, when I was looking for a job and contemplating a Ph.D. and Tad was generously paying me as a research assistant. They have never been published before, although I presented them at the Tadfest in September, 2013. Now seems the right time to finally publish them – thanks to Tad and his 1987 NSERC grant!

Upon returning from Brazil in 1986 Tad also became enchanted with scale-space. No doubt it appealed to his career-long favorite topics of sparsity and robustness, recurring themes in his book with Mauricio Sacchi (Ulrych and Sacchi, 2005). I had also been playing with median filtering and together we combined the ideas of scale-space with those of a cascaded median filter (see Figure 1), resulting in the median decomposition (Leaney and Ulrych, 1987, 1992). As can be seen, edges in median scale-space do not move with increasing scale, conferring several advantages.

The summers of ’86 and ’87 were amazing times, and included work with Oliver Jensen and Colin Walker on non-white deconvolution (Jensen et al., 1988), which incorporates the idea of fractal processes. A few years later Tad presented a paper in Brazil titled “Scale Space, Fractals and a Touch of Chaos” (Ulrych, 1991). The late Mike Schoenberg was at that conference and told me it was one of the best talks he’d ever seen. I know Tad was very proud of it and eventually wrote a related paper for Geophysics (Ulrych, 1999). I encourage the reader to revisit this paper, and enjoy Tad’s engaging and sometimes humorous style of exposition.

At the SEG in 1987 Tad introduced me to Ralphe Wiggins at the party Schlumberger was throwing to celebrate their purchase of GECO and entrance into the surface seismic industry. That introduction ended up getting me my job with Schlumberger; I left UBC in 1988. Tad and I remained in contact and our friendship continued to grow. We met up from time to time at points around the globe, and he visited us in several of our postings. One of the countless late night sessions was in Paris in 1992. There we hatched what Tad referred to as the “Johnnie Walker theorem” (JWT). I remember the sound track to that session was Moe Koffman’s rendition of “Neptune” (1974). (For the jazz buffs out there, check it out.) For those curious as to what the JWT might refer to you can find a page devoted to it in my Ph.D. thesis (Leaney, 2014). The idea of doing a late career Ph.D. is due to a conversation between Tad and my mother that took place at the lake. My Ph.D. thesis supervisor, of course, was to be Professor Emeritus T.J. Ulrych. The last time I was able to visit with Tad was on July 15, 2014, in the hospital, after my Ph.D. defense. We spoke on the phone almost daily until just before his death in August last year.

Figure 3 shows Tad at Lake of the Woods in 2008 discussing the age of the pre-Cambrian shield. It was fun to get Tad talking about old rocks since he got his Ph.D. in lead isotope dating. He told me that for a period of about three months he could lay claim to having dated the oldest rock in the world. I found a date of 3.46 b.y. for a rock in South Africa quoted in Ulrych et al. (1967). Yet another fascinating fact about an incredible man.

Tad’s legendary lust for life is remembered fondly by many, including my family and non-geophysical friends. He never shied away from superlatives when describing colleagues and friends, and now it is my turn. Quite simply, he was the most remarkable person I have ever met.

References

Jensen, O.G, Ulrych, T.J., Todoeschuck, U.P, Leaney, W.S. and Walker, C., 1988, Blueness compensation in deconvolution for the reflectivity sequence: SEG Technical Program Expanded Abstracts, 939-942.

Koffman, M., 1974, Solar Explorations, GRT Records.

Leaney, W.S., 2014, Microseismic source inversion in anisotropic media, PhD Thesis, University of British Columbia. http://circle.ubc.ca/handle/2429/50045

Leaney, W.S. and Ulrych, T.J., 1992, Compound median filtering and the median decomposition: log processing applications: Journal of Seismic Exploration.

Leaney, W.S. and Ulrych, T.J., 1987, Compound median filtering applied to sonic logs: SEG Technical Program Expanded Abstracts, 23-26.

Ulrych, T.J., 1999, The whiteness hypothesis: Reflectivity, inversion, chaos and Enders: Geophysics, 64, No. 5, 1512-1523.

Ulrych, T.J., 1991, Scale Space, Fractals and a Touch of Chaos: Brazilian Geophys. Conf. (SBGF), 866-871.

Ulrych, T.J., Burger, A. and Nicolaysen, L.O., 1967, Least radiogenic terrestrial leads: Earth and Planetary Science Letters, 2, 179-184.

Ulrych, T.J., and Sacchi, M.D., 2005, Information-Based Inversion and Processing with Applications, Handbook of Geophysical Exploration, Seismic Exploration, vol.36. K.Helbig and S.Treitel, Editors, Elsevier, 1-404. Hardbound, ISBN: 0-08- 044721-X, 404 pages

https://www.elsevier.com/books/information-based-inversion-and-processing-with-applications/ulrych/978-0-08-044721-6#description

Witkin,A. P., 1983, Scale-space filtering: Proc. 8th Int. Joint Conf. Art. Intell., Karlsruhe, Germany, 1019–1022