The Influence of the Lithosphere on the Core: 3D Mantle Convection Modelling on Planetary Scales

Abstract

Parallel computing clusters have made it feasible to study three-dimensional mantle convection on time scales of billions of years. Models tailored to take advantage of parallel machines are being used to re-examine problems where the full effects of three-dimensionality have remained unexplored. As a result, it has become possible to solve problems once considered intractable from a computational standpoint. Here, we describe some of the findings from two recent 3D convection studies examining the effect of mantle processes on heat flow from the core. The studies use the parallelised computer codes TERRA and MC3D in order to solve for the evolution of thermal fields in vigourously convecting planetary scale systems. We present results from a study comparing the secular cooling of a planet with a mobile lithosphere, like the Earth, to a planet with an immobile surface, like Venus. The findings show that the mobility of the lithosphere of our planet has a significant impact on the heat drawn from its core. Heat flow from the core into the mantle is intimately related to the vigour of the convection in the outer core that is responsible for the planetary dynamo. Consequently, mantle convection has a controlling influence on the strength of the magnetosphere. We conclude by describing a second study that indicates that a significant contrast between upper and lower mantle viscosity diminishes the impact of surface events on core heat flow and may therefore play a role in stabilising the strength of Earth’s magnetic field over periods of tens of millions of years.

Introduction

Convection currents carrying cold lithospheric material into the lowest depths of the mantle provide the primary means by which heat is removed from the Earth’s deep interior. Radiogenic heating distributed throughout the mantle provides the principal energy source for the convection that is the driving force responsible for plate tectonics, supercontinent assemblage and breakup, volcanism, earthquakes, eustasy and orogenesis (Schubert et al., 2001). Mantle convection influences the Earth’s topography and gravitational field, the geodynamo, the formation of mineral and hydrocarbon resources and the planet’s climatic system. Consequently, it is even responsible for influencing cycles of environmental and biological evolution. In accord, the study of each of these disciplines reveals some expression of mantle convection and, conversely, our evolving understanding of mantle convection can affect conventional views of a diverse range of fields within the planetary and environmental sciences.

Over the past decade, advances in computing power have made it possible for geophysicists to model 3D mantle convection on the spatial scales required for global studies of planetary evolution. Furthermore, studies (Bunge and Richards, 1996; Zhong et al., 2000; Monnereau and Quéré, 2001) now feature calculations that are able to simulate billions of years of evolution and convective overturning with Earth-like vigour. The calculations involved are performed on parallel computing clusters that feature anywhere between tens and hundreds of computational nodes, simultaneously working on obtaining the solutions to a small region of the global problem and intermittently communicating their findings to the memory resources of similarly employed processors. As is often the case in computer modelling studies, the underlying constraint on the problems that can be examined is spatial resolution. In particular, in order to produce a credible model, the cool thermal boundary layer that defines the thermally defined lithosphere, the cold subducting slabs, hot columnar plumes and hot basal boundary layer enveloping the core, must all be adequately resolved in a solution domain of global scale. Typically, these features require minimal uniform grid spacings of the order of 20-30 kilometres in order to adequately resolve the associated temperature and viscosity gradients. As a result, computational grids can require up to 100 million nodes for each scalar field retained during the calculation. Moreover, calculations may require thousands of integrations in order to achieve adequate temporal resolution. Despite the computational demands, such calculations are becoming increasingly commonplace. The modelling allowed has not only resulted in more accurate determinations of the quantitative characteristics of 3D convecting systems with a history of study in laboratory settings, it has opened up avenues of research on problems that are very difficult to investigate or a re otherwise intractable using alternative modelling methods. One of the advantages the computer models have is their ability to incorporate system characteristics like internal heat sources, free-slip inner (basal) and outer (surface) boundary conditions, internal phase changes, pressure and strain-rate dependent rheologies and model tectonic plates. Moreover, 3D computer models can now simulate vigorous convection and temperature-dependent rheologies; once the exclusive domain of laboratory tank experiments. Although the importance of all of the features in the foregoing discussion has long been recognised in convection studies aimed at understanding the thermal evolution of the Earth, studying the influence of each parameter in a medium convecting in a spherical shell geometry with a radially directed gravity field has only recently become manageable. Now, the implementation of new models is making it possible to explore particularly demanding problems, including studies of the secular cooling of entire planets over time scales of billions of years and investigations of the feedback between plate motion and mantle convection over similar time scales (e.g., Quéré and Forte, 2006).

As our knowledge of the geophysical characteristics of other objects in the solar system increases and our understanding of the Earth’s geologic record improves, some of the more puzzling questions posed to geoscientists today stem from how our planet’s evolution has produced features that are different from those manifested by its neighbours. For example, in order to determine how exactly the Earth generates its strong magnetic field it may be informative to determine why Venus and Mars do not have appreciable internally generated magnetic fields. Ultimately, the rate of heat loss from the core to the mantle determines the vigour of the convection that drives the motion in the outer core. Consequently, mantle convection vigour affects magnetic field strength. In the Earth, the system is complicated by variations in heat flow from the core that may be determined by the evolution of the surface tectonic plates. Here, we present the results from a pair of 3D mantle convection studies focussing on the time-dependence of global core heat loss. The separate studies focus on the implications for heat flow from the core based on 1) cooling of the mantle and 2) variations in core heat flux resulting from the influence of plate evolution on mantle convection.

Modelling Method

Each of the studies described models the mantle as a partially basally heated (i.e., overlying a hot isothermal core), incompressible fluid that obtains the majority of its heating from uniformly distributed internal sources. To obtain the evolution of the mantle’s temperature and velocity fields, a coupled system of partial differential equations is solved for the conservation of mass, momentum and energy. The system is completed by an equation of state for the fluid mantle, which has a density that is weakly dependent on temperature but not pressure (the Boussinesq approximation - Chandrasekhar, 1961). We specify a Newtonian viscosity (the proportionality constant in a linear relationship between stress and strain-rate) and thermodynamic parameters fitting mantle rocks. Both of the studies feature depth-dependent viscosities characterised by sharp increases in viscosity below a depth of 670 km (e.g., Hager, 1984). The viscosity values in the deep mantle are a factor of 30 times greater than the upper mantle values. When combined with the specified thermal parameters, viscosity and gravitational acceleration, the prescribed heating rates result in vigorous convection in a momentum-free fluid exhibiting velocities of a few centimetres per year. We present solutions obtained in studies using both spherical shell and Cartesian geometries. The spherical shell geometry solutions are obtained using the mantle convection code TERRA (Baumgardner, 1985). TERRA is a finite element code that solves the equations governing mantle convection on a high resolution grid obtained by refining a series of concentric icosahedra (Figure 1). The grid is determined by adding computational nodes at the midpoints of the line segments joining neighbouring vertices of the icosahedra. Each successively obtained polyhedra can be refined similarly to produce increasingly higher resolution meshes, each featuring triangular surface elements (Figure 2). The Cartesian code, MC3D, solves for the evolution of the temperature, stress and velocity fields using a hybrid spectral/finite-difference code on a rectangular grid featuring uniform horizontal node spacing and a uniform but different vertical grid spacing (Gable et al., 1991). Evolving plates can be included in MC3D’s calculations with the use of an evolving finite element grid that determines the surface mechanical boundary conditions required to model the plates.

The effect of mechanical boundary conditions on the secular cooling of planetary interiors: comparing the histories of the Earth and Venus.

Motivation

It has been suggested that the lack of an appreciable Venusian dipolar magnetic field has resulted from the absence of lithospheric participation in Venusian mantle convection for the past 0.5-0.75 billion years (e.g., Nimmo, 2002). In contrast, terrestrial mantle convection (featuring the subduction of oceanic lithosphere) is particularly efficient at cooling the Earth. Moreover, participation of the Earth’s outer thermal boundary layer in terrestrial mantle convection carries cool material deep into the planetary interior and influences heat flow at the core-mantle boundary. Thus, lithospheric subduction influences the geodynamo that originates with compositional convection in the conducting outer core. In this work, we examine the thermal evolution of terrestrial planets by modelling mantle convection in spherical shells with time decaying heat sources and core cooling. Similar bulk concentrations of U and Th and K/U ratios to those estimated for the Earth are assumed. We consider initial thermal fields that are in a state of cooling and examine the effect of a change in the planet’s mechanical surface boundary condition on its rate of temperature change and core heat flow. The calculations initially feature free-slip (mobile) surfaces. With this condition an initial thermal field featuring steady secular cooling is obtained as a starting point for subsequent calculations. Both the calculations used to obtain the initial fields and the final calculations described here, extend over periods equating with hundreds of millions of years. Two cases are compared: a planet in which free-slip surface motion has been replaced by a rigid mechanical surface and a planet in which surface mobility continues unhindered. By specifying the onset of a period featuring an immobile surface, we implicitly examine the effect of the cessation of the upper lithosphere’s participation in mantle convection. With the absence of surface motion, the extraction of heat from the core-mantle boundary to the overlying mantle is reduced. The modelling suggests that a change in surface conditions could halt thermal convection in the core and hence eliminate the global magnetic field. The results provide insight into events that may be relevant to Venus’s past and also address the question of whether plate tectonics may be a critical ingredient in sustaining the Earth’s magnetic field.

Results

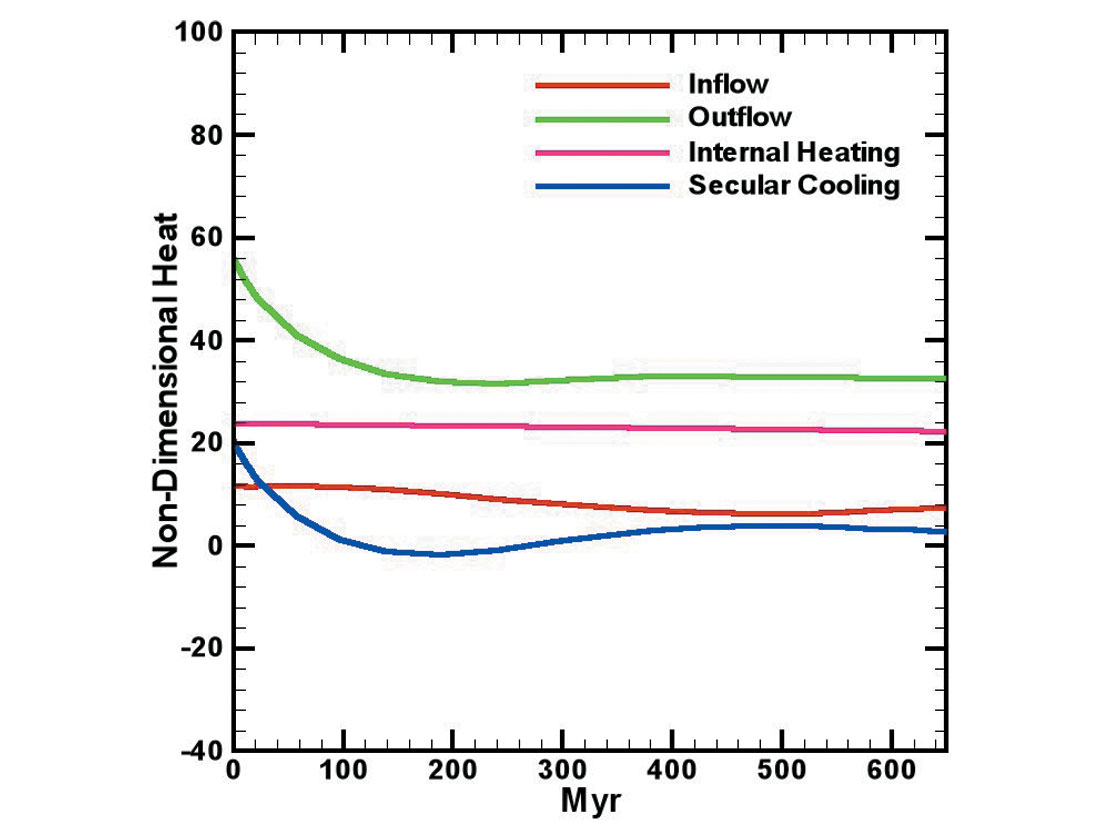
Figures 3a and 3b show the temperature fields from two models started from the same initial conditions. The models feature a depth-dependent viscosity and the mantle is heated by both internal sources and heat flow from the core. The core temperatures are time-dependent and respond to the heat lost to the mantle over the 650 million year time period that the modelling spans. The dimensions of the planets modelled are comparable to the Earth (slightly too big for Venus). The models differ by the imposed surface mechanical boundary conditions. The field for the model shown in Fig. 3a was obtained after the imposition of an immobile surface boundary condition for the preceding 650 Myr. The field in Figure 3b features a free-slip (mobile) boundary at all times. The model featuring a mobile surface is considerably cooler than the model having a stationary surface (indicated by the absence of cool downwellings). The rate of cooling in the models is indicated by the amount of the heat flow from the planet obtained from secular cooling. Secular cooling of the mantle occurs not only because the heat flow from the planet’s core decreases over time (one implication of this is that the radius of the frozen inner core is increasing) but also because the concentration of the radiogenic elements contributing to internal heating is decreasing as the parent isotopes decay into the associated daughter. The global heat flow from the mantle must equal the sum of the heat flow from the core, the heat flow due to internal sources and the heat flow due to secular cooling.

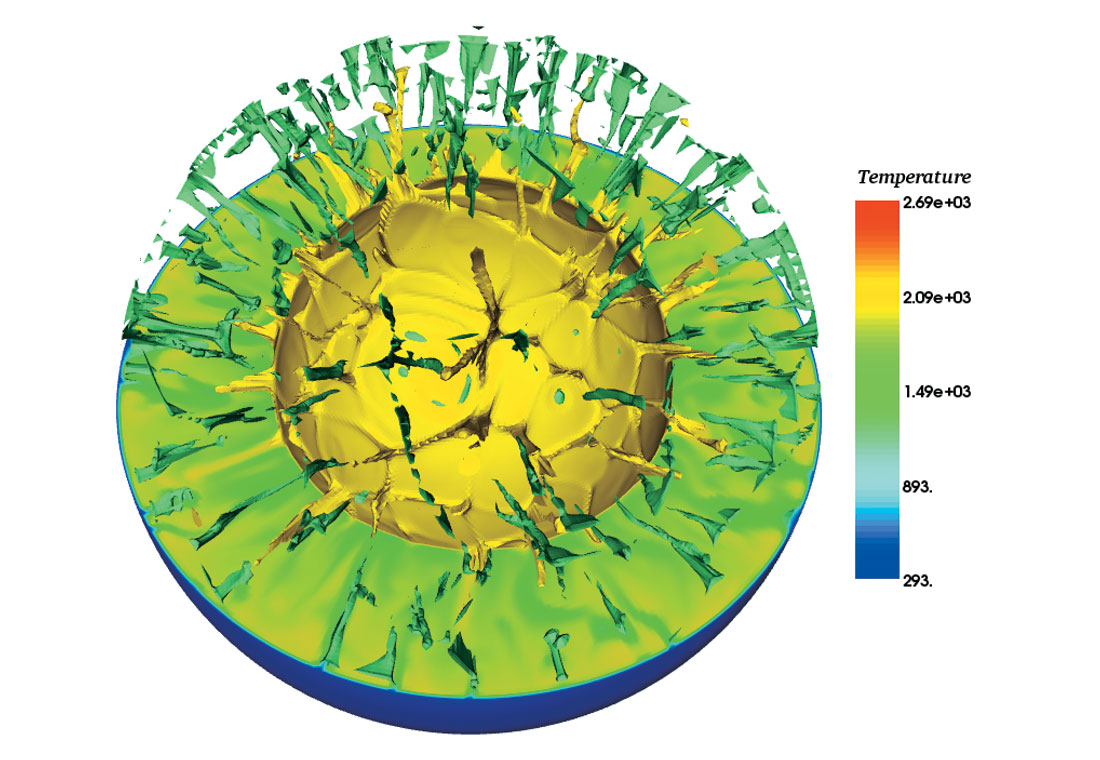
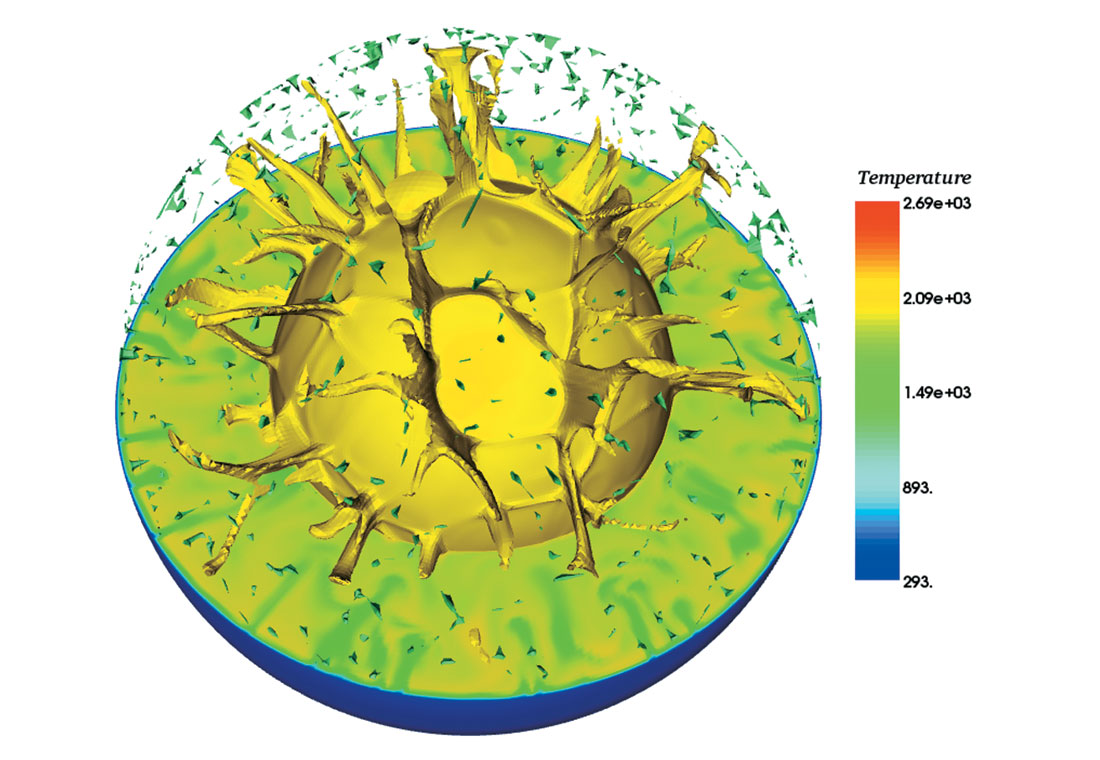
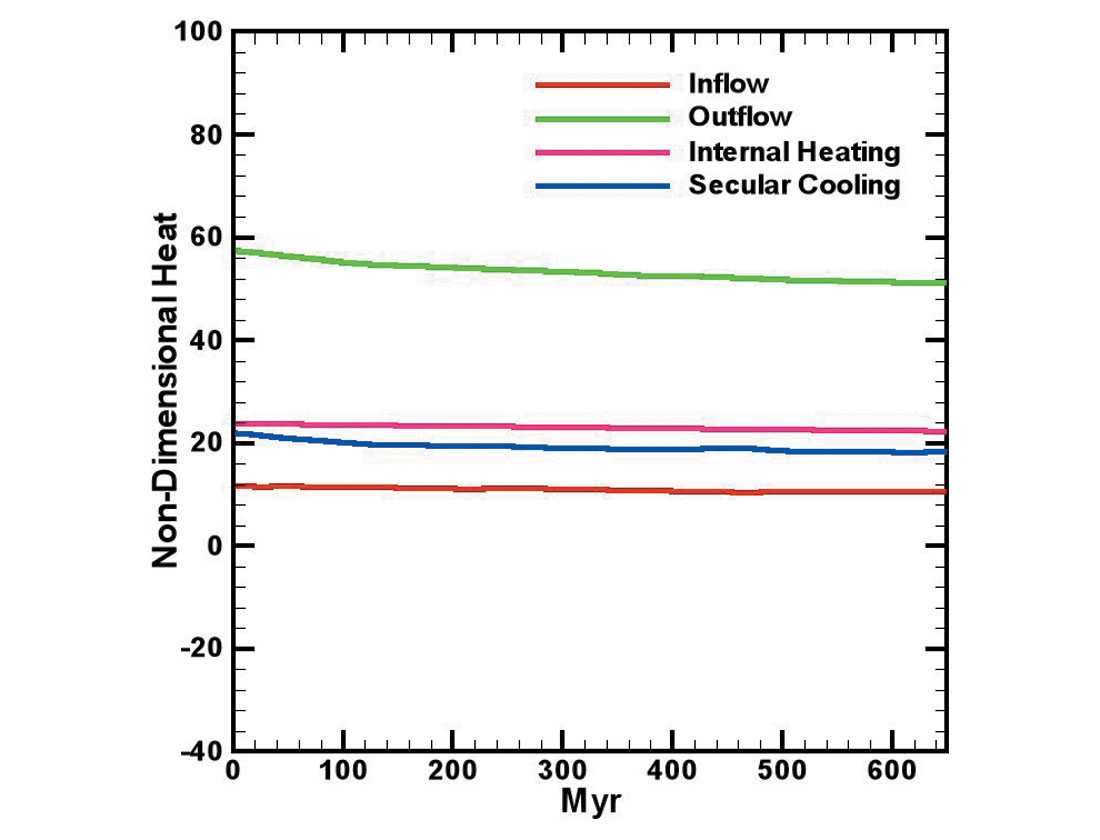
Figure 4 shows the evolution of the individual components that contribute to the total global heat flow for each of the models in Figure 3 during the 650 million year period that the numerical experiments simulate. This study of the secular cooling of Earth and Venus-like planets considered experiments with core cooling and different viscosity stratifications. In all of the cases examined it was found that the transition from a mobile surface to an immobile surface results in a significant drop in both the heat flow from the mantle and the heat flow into the mantle from the core. We observed reductions in heat flow out of the core of up to 70% during the period that elapses between the onset of surface immobility and the final state reached in each calculation - reductions of 50% are typical. Cases that include core cooling were compared to cases in which core cooling was absent. It was found that core cooling has a relatively small effect on the secular cooling of the mantle in the calculations presented. The calculations indicate that the period of mantle heating that would follow the start of surface immobility would not exceed 500 Myr. In this study, we do not find any cases where the change in the surface mechanical boundary condition is great enough to completely halt heat flow from the core.

The feedback between plate motion and mantle convection: do plate reorganization events affect the core?

Motivation

The influence of plate motion on the nature of mantle flow has been studied since the early days of computational mantle convection modelling. It has been firmly established that the rigidly translating plates and the convecting mantle constitute a coupled system featuring a high degree of feedback (e.g., Bercovici, 2003). Plate motion strongly influences the temperature structure (i.e., dominant thermal wavelengths) of the mantle, which in turn contributes towards determining plate velocities. The rigidity of the plates results from the thermally activated rheology of mantle rocks. Thus, the non-crustal lithosphere is the cool upper thermal boundary of the mantle and subducted oceanic plates are the cool downwellings of the convecting system. In the following we describe some of the recent findings from a study of the effect of the contrast between upper and lower mantle viscosity, on core heat flux time series. These mantle convection models feature idealised rigid plates but dynamically determined velocities and evolving geometries.

Results

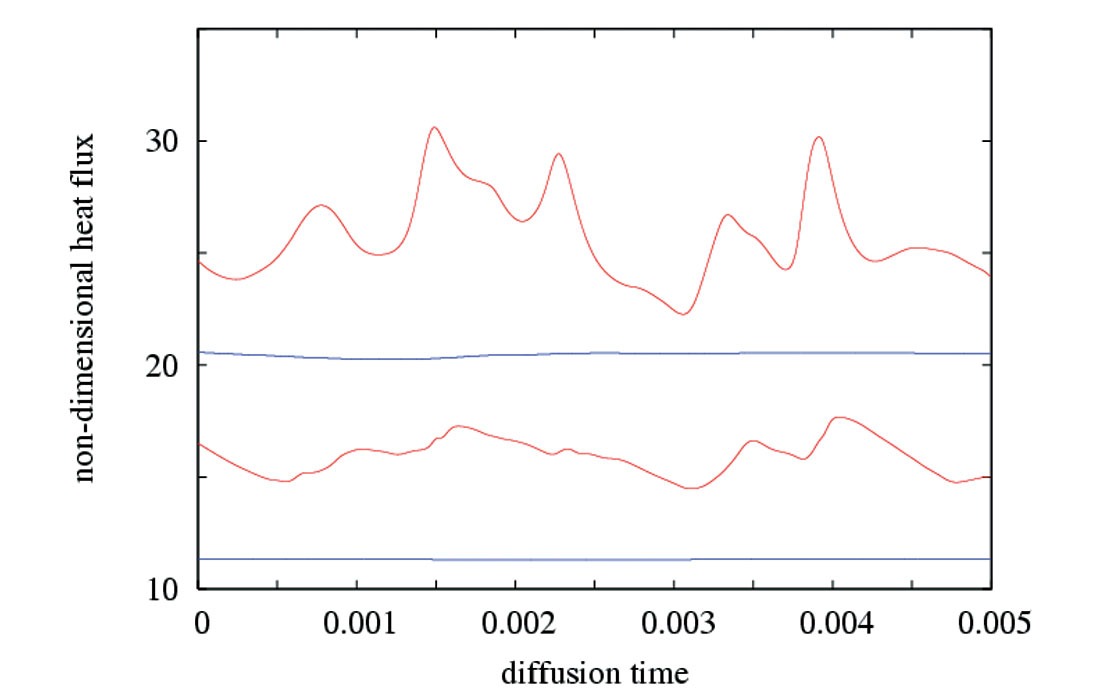
Figure 5 shows two snapshots of the temperature field from a mantle convection model featuring nine plates with dynamically determined evolving velocities (Lowman et al., 2001; King et al. 2002). The plate geometry instills its wavelength on the deep flow. The system is highly time-dependent and features a number of flow reorganisation events (King et al. 2002) characterised by intermittent rapid changes in the surface plate velocity field that punctuate periods of fairly steady flow. The extreme time-dependence exhibited by the model is attributed to the combination of large plates and an internally heated fluid. Plate motion tends to increase the wavelength of the convective flow so that it mirrors the dimensions of the plates themselves. Uniformly distributed internal heat sources produce a diffuse distribution of weak upwelling material that becomes entrained by plate motion into focussed regions enveloping the cold downwelling sheets (the fluid model analogue of subducted slabs). The heat in these regions builds up during periods featuring steady flow patterns and eventually raises the buoyancy of the associated mantle to the point where it overcomes the downward drag of the neighbouring downwelling. When this happens the flow is forced into reorganising and the built-up heat escapes upwards. Subsequently, a source of buoyancy will build elsewhere in the ensuing steady flow pattern and the scenario just described will repeat itself. Reorganisation events are dominated by the appearance of new convergent plate boundaries where young plate is consumed. After being subducted the cold young plate sinks to the bottom of the convecting system, where it spreads over a portion of the coremantle boundary. Consequently, plate reorganisation events are manifested in the time series of the core heat flow from the convection model (Fig. 6). The lower mantle of the model shown (below 670 km depth) has a viscosity that is 30 times more viscous than the upper mantle. Increasing the lower mantle viscosity decreases the system time-dependence. Moreover, the greater time required for cold sinking material to reach the core allows for the cold parcels to warm to values close to the ambient mantle temperature. Thus, flow reorganisation events do not have a dramatic influence on core heat flow if the lower mantle is two or more orders of magnitude more viscous than the upper mantle (Fig. 6).

Conclusions

Surface mobility has a strong influence on the rate of heat extraction from a planetary core. The cessation of surface motion, as has been inferred for Venus, would result in a significant decrease in the heat flow from the core, possibly explaining why Venusian interior dynamics do not support a geodynamo. In contrast, motion of the Earth’s surface and participation of its lithosphere in a mantle wide convection driven circulation allows for a much more efficient removal of heat than is obtained in a planet with an immobile surface. The combination of internal heat sources and plates produces a highly time dependent flow characterised by intermittent reorganisation events. However, the high viscosity of the deep mantle may buffer the core from subjection to variations in heat flux comparable to those that flow reorganisation events must cause at the planet’s surface. Future studies of the evolution of a convecting mantle in models featuring dynamically evolving oceanic and continental plates should clarify the influence and importance of the unique nature of the surface of our planet on the dynamics of its core.

Acknowledgements

Thanks to the following collaborators for their contributions to the studies described: Carl Gable (Los Alamos National Laboratory), Hans-Peter Bunge (The Ludwig-Maximilians Universität, Munich), Scott King (Purdue University), Dan Nettelfield and Andrew Gait (The University of Leeds).