Summary of the Poisson’s Ratio Debate 1990 – 2003

Poisson’s ratio

This relationship was defined by Poisson in 1829 as follows:

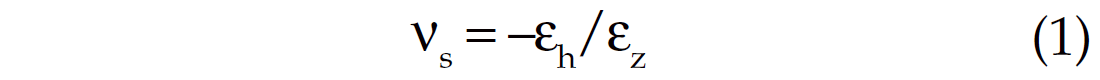
where

ν_s is the static Poisson’s ratio
ε_h is the lateral strain ΔR/R (expansion)
ε_z is the axial strain ΔL/L (contraction)

These are all for an unconfined core under axial stress and this is a static test (the minus sign makes Poisson’s ratio a positive number).

Provided the core material is linearly elastic, homogeneous and isotropic* the Poisson’s ratio may also be defined in terms of V_p/ V_s, which I prefer to call the PS Ratio or PSR for short:

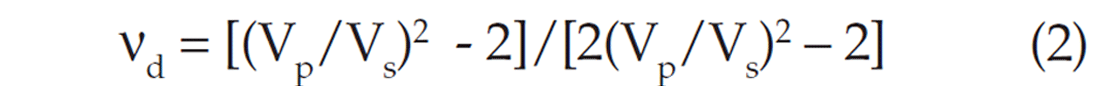
or

where ν_d is the dynamic Poisson’s ratio. If the above proviso is fulfilled, as, e.g., for metals, we have:

The Poisson’s ratio is not a spectacular property; it ranges from 0.05 to 0.20 for very strong materials and reaches a value of 0.5 for fluids with no shear strength. Compare this to seismic velocities ranging over an order of magnitude or even electrical or hydraulic conductivities covering many orders of magnitude.

Poisson’s ratio users

Poisson’s ratio appears regularly in the literature of the AVO analysts and the geomechanists. The former use exclusively the dynamic Poisson’s ratio, a natural fall out of modern Vp and Vs recording. The geomechanists rely on the static Poisson’s ratio for stress analysis, in particular to assess lateral rock stresses. Measuring the static Poisson’s ratio is cumbersome and few values exist in the literature and there is a great temptation to use the abundant dynamic Poisson’s ratio values available. In all fairness it must be stated that in recent years the underlying assumptions for using Poisson’s ratio in rock mechanics have been questioned and the importance of this parameter has declined (see The Debate).

The Debate

It all started with Leon Thomsen’s short note in 1990. He appealed to the AVO analysts to abandon the term “Poisson’s ratio” since, in his opinion, it is both confusing and unnecessary. He made his plea in no uncertain terms as the following quotes demonstrate:

“The purpose of this Round Table essay is to argue that Poisson’s ratio is not relevant to any problem in seismology, and that we should clear our minds of it, and of the confusion it entrains.”

“There is not a single seismological equation where Poisson’s ratio enters in a natural way.”

“Let us leave Poisson’s ratio to the mechanists, for whom it was designed, and keep it out of seismology.”

This strongly worded request drew only a single reply from Todd (1991), who states:

“However, the relationship between Vp/Vs and Poisson’s ratio is straight forward and, in practice, I’ve found it possible to move back and forward between the two with relative ease.”

In my opinion this relationship is anything but straight forward and he misses the point.

Thomsen (1991) in his reply defends the elimination of Poisson’s ratio in the interests of mathematical clarity and transparency. He also points out that the Hilterman equation (which involves the difference in Poisson’s ratio between the media on either side of a reflecting interface) [Hilterman, 1990] is based on questionable assumptions. This again does not get to the heart of the matter.

In summary, Thomsen was ignored and AVO analysts continued to write about Poisson’s ratio as they have done ever since the early paper of Muskat and Meres (1940).

In 1994 I noticed that some of the numerical values for Poisson’s ratio that had been reported in the geophysical literature simply were not acceptable from a mechanical point of view.

Norm Domenico gives ν_d = 0.1 for a dry sand pack and ν_d = 0.4 for wet sandpack (1976, 1977) while Gregory (1976) even lists negative values for dry sandpacks.

This raises two points:

Point #1: Low values for Poisson’s ratio (0.05 to 0.15) are typical for high strength rocks such as basalt, granite, quartzite, etc. (negative values are physically absurd). This is even recognized by the AVO fraternity (Engelmark, 2000). The low value for dry sand packs seems to have troubled nobody with the notable exception of Ostrander (1984) who writes: “…gas saturated high-porosity sandstones tend to have abnormally low Poisson’s ratios on the order of 0.10.”

Point #2: From soil mechanics we know that the angle of repose of dry and wet sand is the same, which implies equivalence of the Poisson’s ratio. When laterally confined, such as in a bin or by aerially extensive sediment (ε_h = 0), the lateral stress in a cohesionless sand pack is given by:

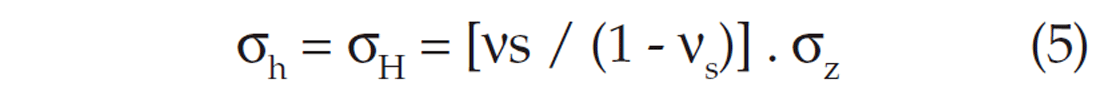
where:

σ_h = σ_H is lateral stress
σ_z is overburden stress*
ν_s is the static Poisson’s ratio
*in the submerged stage the concept of effective stress applies (σ_z = S_z – p; S_z is total overburden stress, p is pore pressure).

This lateral stress remains the same wet or dry except that in the wet case the buoyant weight enters the equation.

In 1995 Domenico wrote a rebuttal in which he stated: Gretener’s argument (1994) is that the ratio of compressional-wave to shear-wave velocity (Vp/Vs) is not an indicator of Poisson’s ratio and he attempted to demonstrate that Poisson’s ratio must be the same for dry and wet sands. This, if true, is devastating to AVO theory (as developed, for example, by W. J. Ostrander in Geophysics in 1984…).

Nobody found it necessary to respond. Norm and I decided some brains were needed here and thus asked Leon Thomsen for a second opinion. His note appeared in the TLE in 1996. With question marks in the final equation it, in my opinion, still left something to be desired.

By the year 2002 there was no further discussion and the use of Poisson’s ratio continued unabated in the AVO literature (see, e.g., Engelmark, 2000; Dutta, 2002).

Thus followed the final (for the time) discussion (Gretener, 2003; Thomsen, 2003) in which I simply stated that for rocks we have:

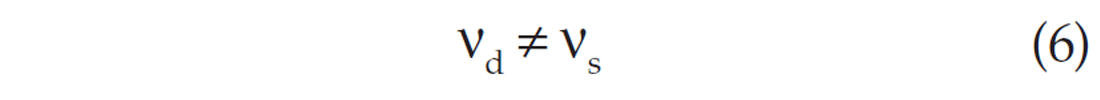
For equation (3) to be valid a material must be both linearly elastic and homogeneous. Rocks are neither and equation (3) is not valid. In particular, the difference noted between the dry and the wet sand pack is caused by its heterogeneity (a two phase system). The pore filler being a fluid is always in the state of stress called “pressure”. Mechanically the pressure is important (concept of effective stress) but the nature of the fluid (gas/air vs oil/brine) is irrelevant.

In contrast, seismic wave propagation “sees” the type of fluid (the essence of 4-D seismic data). Thus, as gas replaces liquid, the P-wave velocity collapses (e.g. Domenico, 1995, p.984, Fig.1) and that accounts for the drastic change in Poisson’s ratio.

This is not a new discovery insofar as the time-average equation of Wyllie (1963) has served us well over many decades in the heterogeneous material of porous rock. The important aspect of Domenico’s papers (1976,p 884, Fig 1; 1977, p. 1361, Figs. 24 and 25) was to demonstrate that the Wyllie equation does not work for a 3- phase system (gas/liquid/rock) or, as I put it, a geophysical gas-sand is not necessarily a commercial gas-sand. The implications for the Poisson’s ratio went unnoticed in the shadow of this most significant observation.

Consequences

Fortunately, Domenico (1995) is wrong in his statement that abolishing the Poisson’s ratio is devastating to AVO analysis. AVO analysts never really deal with Poisson’s ratio, they assume, use and measure the PSR. Dutta (2002) must only relabel his ordinate in terms of PSR. The Hilterman equation (Hilterman, 1990) can be written in terms of ΔPSR rather than Δσ (he uses σ for Poisson’s ratio). There is no effect on AVO analysis except that ν_d = Poisson’s ratio is a misnomer.

The geomechanics fraternity will have to stick to νs. Poisson’s ratio is no longer very important since numerous well measurements indicate equation (5) to be of limited value as we generally find σ_H > σ_h, indicating that an active tectonic component of compression or extension is usually present.

Only the Fracture Height log seems to be affected by the above conclusions. It relies on PSR derived Poisson’s ratio for a mechanical analysis which seems inappropriate (Ahmed, 1988)

Bottom Line

Leon Thomsen’s comments of 1990 are fully supported and it is time to implement them. This is not just a matter of convenience but a case of good or bad physics. As I said in 1994, the PSR is a legitimate and important physical property of any material but….. only if this material happens to be linearly elastic, homogeneous and isotropic will it also provide the Poisson’s ratio.

*The issue of elastic anisotropy never entered the debate. However, aligned cracks (joints) are a ubiquitous feature of virtually all rock masses and this leads us to anticipate elastic anisotropy and the associated shear wave splitting to be a wide spread phenomenon (Crampin, 2003). The effect is most pronounced when such cracks are open, in which case they also profoundly affect the fluid flow.