Stereotomography: Past, present and future

Abstract

Stereotomography was proposed seven years ago for estimating velocity macro-models from seismic reflection data. Initially the goal was to keep the advantages of standard travel time tomography but remedying for difficult interpretative travel time picking. Stereotomography relies on the concept of locally coherent events characterized by their local slopes in the prestack data cube. By now, stereotomography has been developed in 2D and 3D, and useful experience gained. The initially expected advantages of the approach have been fully demonstrated (in particular semi-automatic stereotomographic picking strategies have demonstrated their efficiency) but further studies have also considerably increased the potential and flexibility of the method. For example, now stereotomographic picking can be done either in the pre-stack or post-stack domain and either in the time or depth domain. Finally it appears that the theoretical frame of stereotomography allows reconciliation, in a very satisfactory and efficient way, of most of the methods proposed for velocity macro-model estimation for depth imaging. Moreover an extension of the method to full waveform inversion already exists and promises very interesting developments.

Introduction

We initially proposed stereotomography (Billette and Lambaré, 1998) as a robust tomographic method for estimating velocity macro models from seismic reflection data. We had recognized the potential efficiency of travel time tomography (Bishop et al., 1985; Farra and Madariaga, 1988) but also the difficulties associated with a highly interpretative picking. The selected events have to be tracked over a large extent of the pre-stack data cube, which is quite difficult for noisy or complex data.

The idea was to use locally coherent events characterized by their slopes in the pre-stack data-volume. Such events can be interpreted as pairs of ray segments and provide information about the velocity model independently (Figure 1). This idea has already been investigated by Russian geophysicists (Riabinkin, 1957) and was more recently revived by Chuck Sword from Stanford University (Sword 1987). The method was called Common Directional Reception (CDR) and is still used in some industrial seismic processing tools (Whiting, 1998).

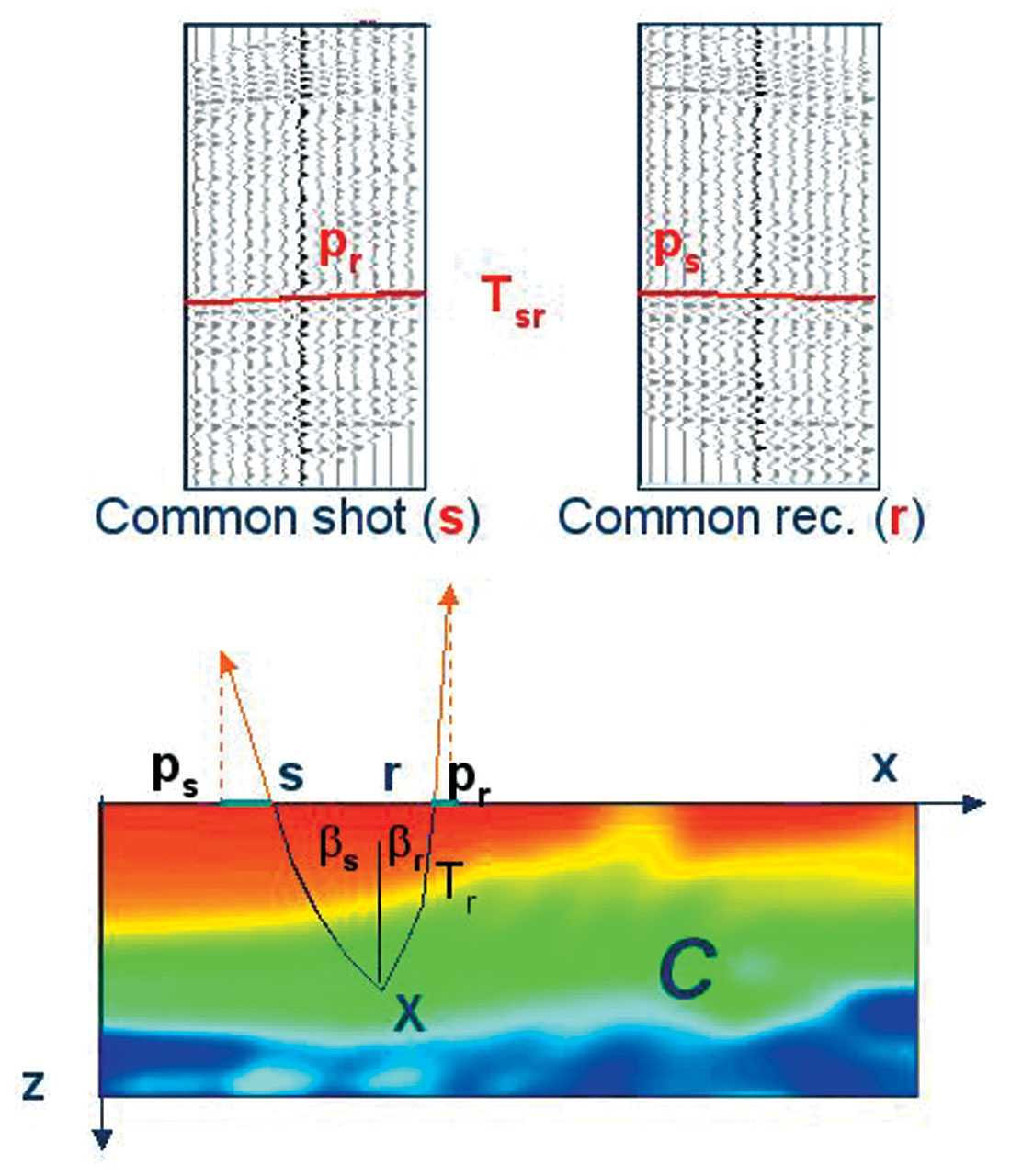
In fact, stereotomography is a generalization of CDR, with the expected benefits of robustness and simplification [for example, the extension to 3D is straightforward (Chalard et al., 2000)]. The introduction of paraxial ray tracing (Farra and Madariaga, 1987) was the other significant improvement since it provided an efficient solution for the numerical computation of Fréchet derivatives (the stereotomographic matrix).

Seven years after our first paper on stereotomography we have gained significant experience on its practical and theoretical uses. 2D and 3D stereotomographic algorithms have been developed and applied on various synthetic and real datasets (Billette et al., 2003; Alerini et al., 2003; Lambaré et al., 2004a).

Stereotomography has also been extended to converted waves (Alerini et al., 2002) and direct arrivals (Gosselet et al., 2003) but conceptually the most interesting extensions concern picking. Initially applied in the prestack time domain (Billette and Lambaré, 1998; Billette et al., 2003), it has been demonstrated that stereotomographic picking can be done in the depth migrated domain (Nguyen et al., 2003) or in the post-stack time domain (Lavaud et al., 2004).

In this abstract I first recall the basis of stereotomography. Then I present the various developments performed on the method, leading to a very efficient and general frame for velocity macro-model estimation. Finally I discuss the advantages and difficulties of stereotomography and present perspectives.

Stereotomography

Stereotomography belongs to the family of slope tomographic methods (Riabinkin, 1957; Sword, 1987; Billette and Lambaré, 1998). The basis of these methods is to recognize that any locally coherent event characterized by its travel time and its two slopes provide some information about the velocity model.

A stereotomographic dataset, d, consists of a set of data parameters

d = [(s, r, T_sr, P_s, P_r)_n]_n=_1,N

of picked locally coherent events parameterized by source and receiver positions, s, r, travel time, T_sr, and the slopes of the event in the common receiver and common shot directions, P_s, P_r (Figure 1). For any event, number n, can be associated, in the exact velocity model, with a pair of ray segments parameterized by

(X, β_s, β_r, T_s, T_r)_n

where X denotes the position of the reflector/diffractor, s, r the ray shooting angles from X towards s and r, and T_s, T_r the two one-way travel times from X towards s and from X towards r (Figure 1).

There are many ways of using the information of the stereotomographic picks. CDR considers the misfit on a single type of data parameter (travel time, slope or position). In stereotomography the cost function consists of squared misfits on all the types of data parameters (Billette and Lambaré, 1998):

C(m) =||d_calc (m) – d_obs||² + Regularization(m).

This choice allows the introduction of uncertainties on all the types of data and theoretically insures the robustness of the local optimization. But, as a consequence, the pairs of segments of rays have to be optimized jointly with the velocity macro-model, which increases considerably the number of model parameters.

Finally, the stereotomographic model is a velocity macro-model, [C_m]_m=1,_M, plus a set of pairs of ray segments associated with each picked event,

[(X, β_s, β_r, T_s, T_r)_n]_{n=1, N}

As in standard travel time tomography, an iterative non-linear local optimization scheme is used for optimizing the stereotomographic model. The computation of the Fréchet derivatives is based on paraxial ray tracing (Farra and Madariaga, 1987) and requires some smoothness of the velocity macro-model. In all our numerical implementations we use smooth velocity macro - models defined by cubic cardinal Bsplines. There is no need for interfaces but if necessary they could be introduced as soon as they are sufficiently smooth.

In order to mitigate the non-linearity, in our local optimization scheme (Figure 2) we first optimize for the pairs of ray segments fixing the velocity macro-model to its initial value. It is the localization step that allows us to greatly reduce the cost function before the joint inversion of velocity and pairs of ray segments. For this joint optimization we use a conjugated gradient optimization, taking advantage of the large sparse matrices involved in the stereotomographic inverse problem (Billette et al., 2003), i.e. the LSQR scheme (Paige and Saunders, 1982). Some regularization also has to be introduced to insure the robustness of the optimization scheme, and we also use a multi-scale approach for the velocity macro-model (Billette et al., 2003, Lambaré et al., 2004a).

Stereotomography has been implemented in 2D (Billette et al., 2003) and 3D (Chalard et al., 2002), together with an automatic slope-picking tool. The important point for the extension to 3D was to demonstrate that a 3D velocity macro-model could be obtained even if a single lateral slope was available from the acquisition geometry (Figure 3). This was the important contribution of Chalard et al. (2000), who also showed the first application of 3D stereotomography to a real dataset (Chalard et al., 2002).

In parallel to the studies aiming at improving stereotomographic picking in the prestack data-cube, important studies have been also done to investigate stereotomographic picking in the prestack depth migrated cube, which is frequently recognized as the most natural domain for the model building process. Indeed the pre-stack depth migrated cube, consisting of gathers of Common Image Gathers (CIGs) is analogous to the pre-stack data cube. Locally coherent events can also be observed and picked in the migrated cube. Schematically, when compared to stereotomographic picking in time (Figure 4), the travel time is replaced by the depth, the positions of source and receiver are replaced by the position and offset of the event, and the two slopes are replaced by the dip in the Common Offset Image (COI) and the slope in the CIG.

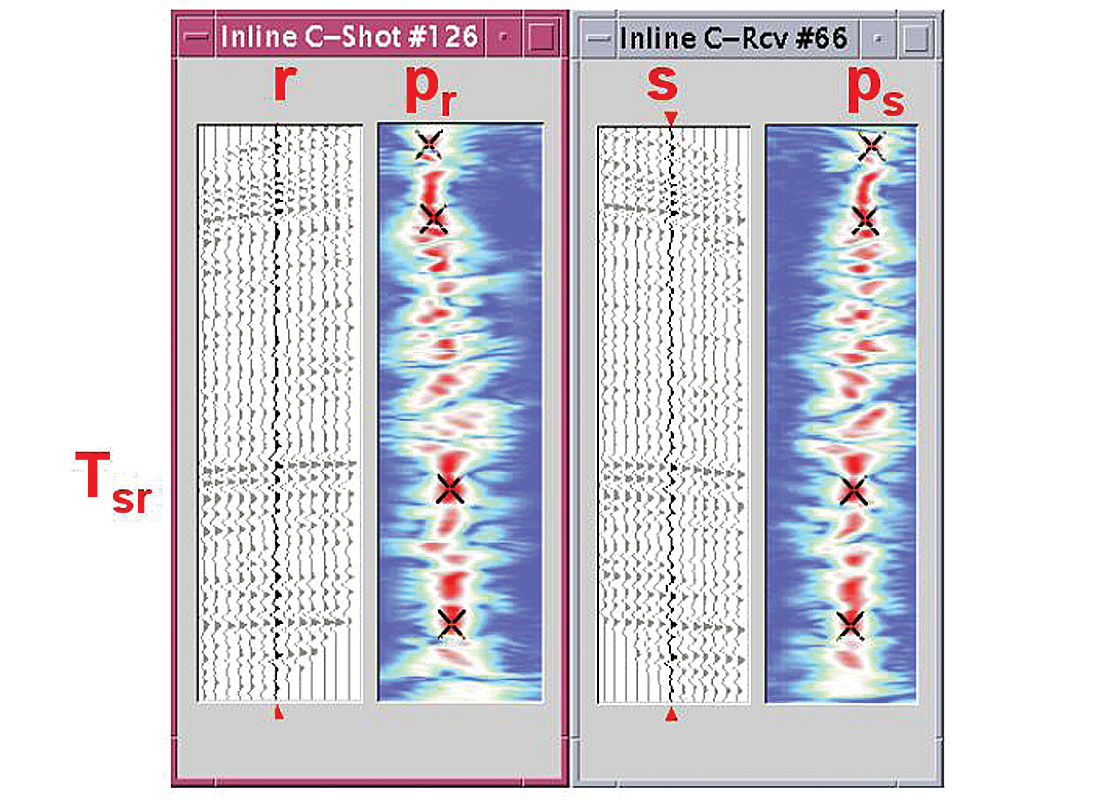
The direct connection between the data picked in the both spaces was a very important contribution by Chauris et al., (2002a, 2002b). It offered a beautiful reconciliation between the travel time based approaches and the image based approaches of velocity macro-model estimation for depth imaging. Practically it also meant that the same stereotomographic optimization code could be fed equally by stereotomographic data picked in the pre- stack time or pre-stack depth migrated domains (Nguyen et al., 2003).

The connection between stereotomographic data and local parameters in the depth migrated cube is also very helpful in the selection of the stereotomographic events during the optimization process. For example the local slope in the CIGs can be used to discriminate primaries from water bottom multiples (Figures 5, 6 and 7) or PS from PP events in PP-PS stereotomography (Lambaré and Alerini, 2005).

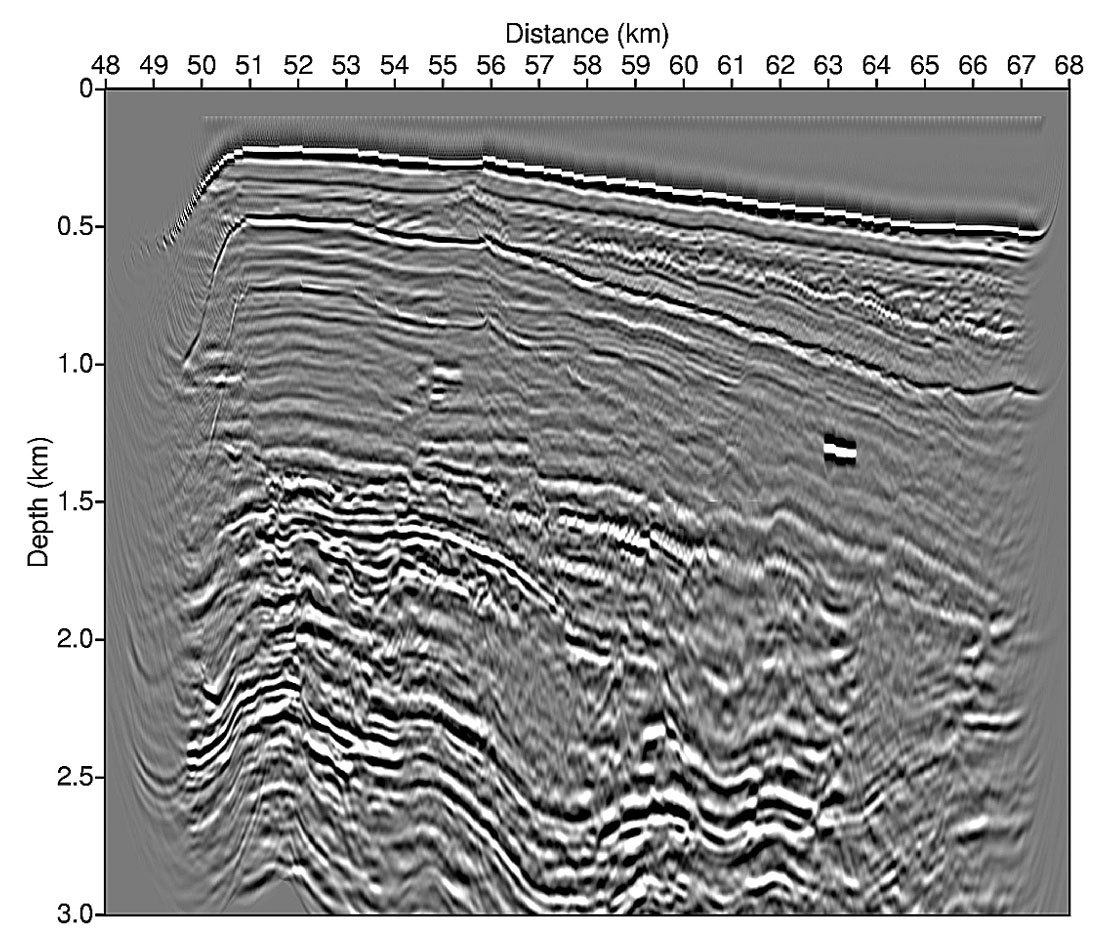
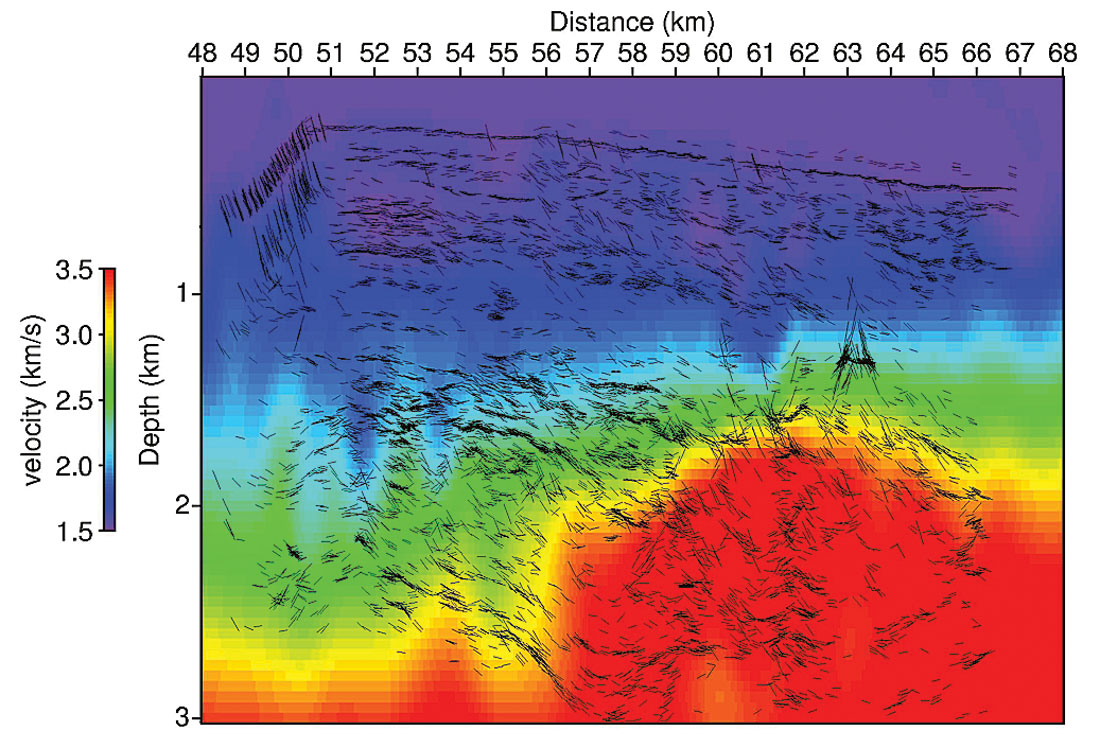
However, picking in the depth domain for a given velocity macro-model insures a regular coverage of the model and also may allow an easier interpretation (i.e., selection) of the events (Nguyen et al., 2003).

Finally, stereotomography appears to be a very effective kernel for handling many types of cinematic information. Indeed, from many parametric representations of travel times or depths in various domains, it is possible to build a stereotomographic dataset simply using the local information. For example, Lavaux et al., (2004) proposed a “post-stack” stereotomography, where the stereotomographic dataset was built from a CRS profile and CRS attributes. The approach was improved by taking into account residual kinematic variations around the CRS curves (Neckludov et al., 2005).

Discussion and perspectives

Several years of developments, investigations, and practice of stereotomography changed significantly our assessment of the method. However, we have been successful in demonstrating the expected advantages of the method:

Robustness and easy extension to 3D when compared to original CDR (Chalard et al., 2000);

Easier and denser picking when compared to standard travel time tomography (Lambaré et al., 2004a).

In addition a powerful theoretical and practical frame has emerged. Stereotomography now allows the reconciliation of time and depth domain methods, and post-stack and prestack methods. The concept that allows for these reconciliations is the local analysis of the data. In practice, most of the types of information used in the other velocity macro-model estimation methods ( residual curvature of CIGs, stacking velocities, pre-stack times, etc) can be used in stereotomography. The only requirement is that the dataset contains sufficient local derivatives. This great ability of the approach is due to a very simple and direct connection between data and velocity model through the concepts of locally coherent events and pairs of ray segments. Recently several variations of slope tomography have been proposed (Biondi, 1992; Guitton et al., 2004; Duveneck, 2004), dropping somehow the local aspect of the methods. I am convinced that this characteristic should be preserved at least in the inner core of the algorithms. Actually, if somebody has to develop a numerical algorithm for velocity macro-model estimation, I would advise him to base it on stereotomography and to use conversions schemes of kinematic information into stereotomographic data.

As it was introduced, stereotomography is a ray based method, with the classical limitations of ray based methods in complex media. However, the principle of a local analysis of the data is not limited to picked data and the potential extension of the method to full waveform inversion has already been recognized by Symes (1998) and Chauris (2000). They emphasized in particular the connection of stereotomography with Differential Semblance Optimization (Symes and Carrazone, 1991; Symes, 1998; Chauris and Noble, 2001; ), which could be then the basis for a natural extension of the method to full waveform inversion.

Certainly much remains to be done for the practical use of stereotomography. For example, we have never fully succeeded in recovering really complex velocity models like Marmousi (Billette et al., 1998; Chauris et al., 2001). Is it due to the nonlinearity of the problem? ... to an intrinsic limitation of ray theory? ... to the inefficiency of the stereotomographic picking? ... Further investigations are required!

Certainly both steps of stereotomography, stereotomographic picking and stereotomographic optimization, can be improved. Concerning the picking, which remains a serious bottleneck (even if it exhibits a real improvement when compared to standard travel time tomography!), investigations should continue in the direction of semi-automatic strategies, which mix various types of kinematical information. Concerning the optimization, improvements should allow the introduction of reliable a priori information (on model and data!) and also the introduction of more general velocity models with anisotropy and discontinuities.

Finally, the combination of various types of data, such as wide angle (Trinks et al., 2002), VSP data (Gosselet et al., 2003) or multi-component data in PP-PS stereotomography (Alerini et al., 2002, 2003; Lambaré et al., 2004c; Lambaré and Alerini, 2005) have already demonstrated their potential and should continue to be investigated.

Acknowledgements

Stereotomography has been developed in the Centre of Geophysical Research of the School of Mines of Paris. I am very grateful to my colleagues and to the students of our laboratory for their enthusiastic adhesion to the stereotomographic method.

Stereotomography was initially developed in the frame of the Joule European projects RODT and 3D FOCUS. Development of stereotomography has been supported by FSH (French Ministry of Industry) and CGG, and from 2001 to 2005 by the sponsors of the DIG consortium. I would like to thank all of them for their scientific and financial support, and also for the various datasets provided by Norsk Hydro, CGG, IFP, Elf, Total, and bp.