Seismic discontinuity attributes and Sobel filtering

Mapping geologic edges such as faults or channel levees forms a critical component in the interpretation on 3D seismic volumes. While the more prominent features can often be easily visualized, smaller features critical to understanding the structural and depositional environment can be easily overlooked. Careful manual interpretation of such features is both tedious and time consuming. Seismic discontinuity attributes that enhance edges not only accelerate the interpretation process, they also provide a quantitative measure of just how significant a given discontinuity is in relation to others. Since seismic attributes extract all subtle features in the seismic amplitude volume, preconditioning the data to enhance geologic edges and minimize edges due to acquisition and processing is critical to the analysis.

In the present work, we find the application of a Sobel filter to energy-ratio coherence volumes significantly sharpens faults and channel edges of interest. We demonstrate this simple cascaded workflow with examples from Kuwait and Canada, where one of the objectives is to provide improved attributes for subsequent automatic fault plane extraction.

Introduction

The preconditioning of seismic data is essential for the generation of seismic attributes. Its importance has gradually been realized over the last decade and has reached a stage where preconditioning of the data has now become a regular practice. A wide variety of preprocessing steps are run on the seismic data to ensure an effective performance of the discontinuity attributes. These range from suppression of spatial noise (random as well as coherent), through approximating missing data that give rise to acquisition footprint through 5D interpolation, to running structure-oriented edge-preserving filtering (Chopra and Marfurt, 2008, 2013).

Sobel filters are one of many filters that are commonly distributed when you purchase a digital camera. For a flat photograph containing pixels of amplitude a aligned along the x and y axes, the classical Sobel-filtered image, s, is simply

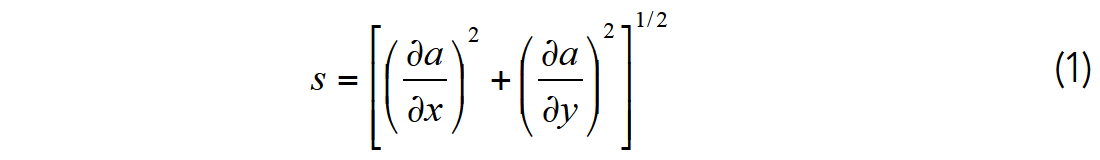
Unlike a photograph, seismic images have a third dimension. In the presence of structural dip, applying equation (1) to a seismic amplitude time slice would result in strong changes as the wavelet varies laterally from peak to trough, overprinting lateral changes in reflectivity of interest. One way to address this issue is to normalize equation (1) by a measure of the RMS amplitude within the same seismic window. Luo et al. (1996) developed the first such Sobel filter based similarity (or coherence) algorithm. Subsequent Sobel filter based coherence similarity algorithms followed advances in semblance based coherence and are routinely computed along structural dip.

In spite of the “structural leakage” associated with computation without regard to dip, Aqrawi and Boe (2011) show some remarkable images using a simple 3D Sobel filter

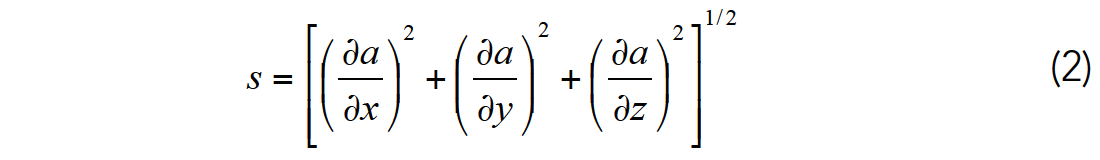
that is balanced by the amplitude of the data within the analysis window.

Recent interest in structure-oriented filtering has resulted in a reexamination of this basic filter. Rather than “smooth” along dip and azimuth, Al-Dossary and Al-Garni (2013) designed a structure-oriented Sobel filter wherein the derivatives are computed in nine non-orthogonal directions, ξ. The output “edge” attribute is the absolute value of the largest derivative of the nine.

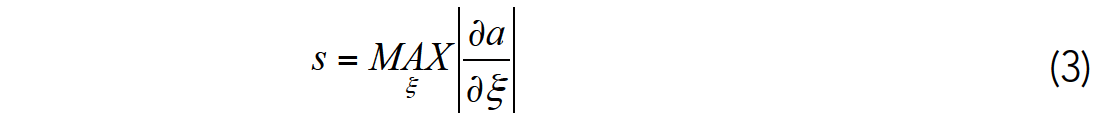
Unlike Luo et al.’s (1996) Sobel-filter coherence algorithm, equations 1-3 are not normalized by the RMS amplitude of the trace and thus provide a stronger response to an edge cutting a high-amplitude reflector than an edge cutting a low-amplitude reflector.

Application

We apply these attributes on a 3D seismic volume from south-east Kuwait. At the level of faulted and fractured Ratawi shale (~1300 ms), we display time slices through the input seismic amplitude volume (Figure 1a), and the results of the Sobel filter (Figure 1b) and energy-ratio coherence (Figure 1c), both computed from the seismic amplitude volume. Notice that the Sobel filter time slice looks very similar to the common semblance-based coherence, and shows the faults and large fractures clearly, which are not so clear on the seismic time slice. Barnes (2007) recognized that many of our attributes can often be redundant, such as shown in this Figure. Sobel filter and semblance-based coherence algorithms are sensitive to lateral changes in amplitude and waveform. In contrast, energy-ratio coherence is only sensitive to lateral changes in waveform. If our stratigraphic features of interest fall below thin-bed tuning, the waveform no longer changes, such that we see more “features” in Figure 1b. In contrast, the lateral resolution of Figure 1c is somewhat sharper. The differences are clearly seen in Figure 2, a stratal slice through a different survey. Here subtle stratigraphic features appear stronger using the Sobel filter while the larger faults and fractures are much clearer on energy-ratio coherence. In this image, the two attributes are no longer redundant, but complementary.

Ant tracking method is frequently used by interpreters to automatically extract faults from discontinuity attribute volumes. Aqrawi and Boe (2011) demonstrated that the application of ant tracking on Sobel-filter output yielded a better fault interpretation than on a similar fault interpretation carried out on a variance attribute. Having seen the Sobel filter displays in Figures 1 and 2, this is not surprising. However, given the sharper fault delineation using energy-ratio coherence we expect the ant tracking to work even better on these images.

Cascaded Filters

Since the classical Sobel filter is routinely used in sharpening photographic images, we hypothesize that we can do the same by applying it to edge-sensitive seismic attributes such as coherence. We can achieve this goal by simply cascading the two attribute calculations. First we apply energy-ratio coherence to the original seismic amplitude to obtain good quality fault and channel edges. We then take the output coherence image and use it as input to a Sobel-filter run along structural dip, thereby further sharpening any anomalies. This workflow can be used to more rapidly delineate channels, or to automatically detect of faults using modern image processing tools.

The data going into coherence computation are usually preconditioned using structure-oriented filtering, reducing the risk of enhancing aligned noise showing up as edges. In Figure 3 we show a comparison of time slices from a 3D seismic volume from central Alberta. Figure 3a shows a time slice through a coherence volume calculated using the energy ratio algorithm where we see a suite of en echelon faults. As this display is at the level of a coherent reflector, we see high coherence everywhere except at the location of the faults. Figure 3b, shows the result of applying a Sobel-filter to the coherence volume. Notice the overall clarity with which the faults now show up as well as some of the other events around them.

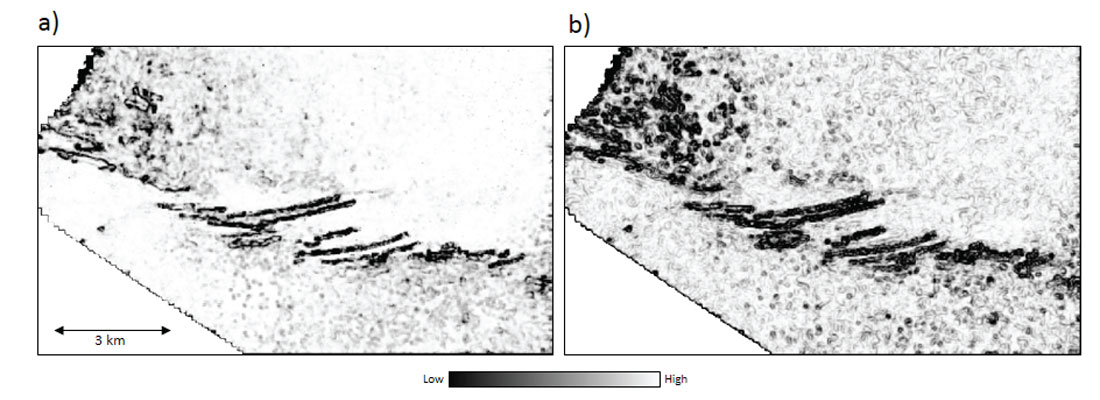
In Figure 4 we show a similar comparison of coherence run on a 3D seismic volume from south central Alberta, Canada but now with the objective of illuminating Mannville channels that traverse the display. In addition to the two main channels indicated with yellow arrows, there are some thin channels indicated by green and blue arrows that crisscross the main channels at many places. In Figure 3b we show the result of applying the Sobel filter to the coherence volume. Notice the crisp definition of the channels on this display. Besides the main channels many of the narrower channels are seen clearly. Invariably, the definition of all the channels on the display is very prominent.

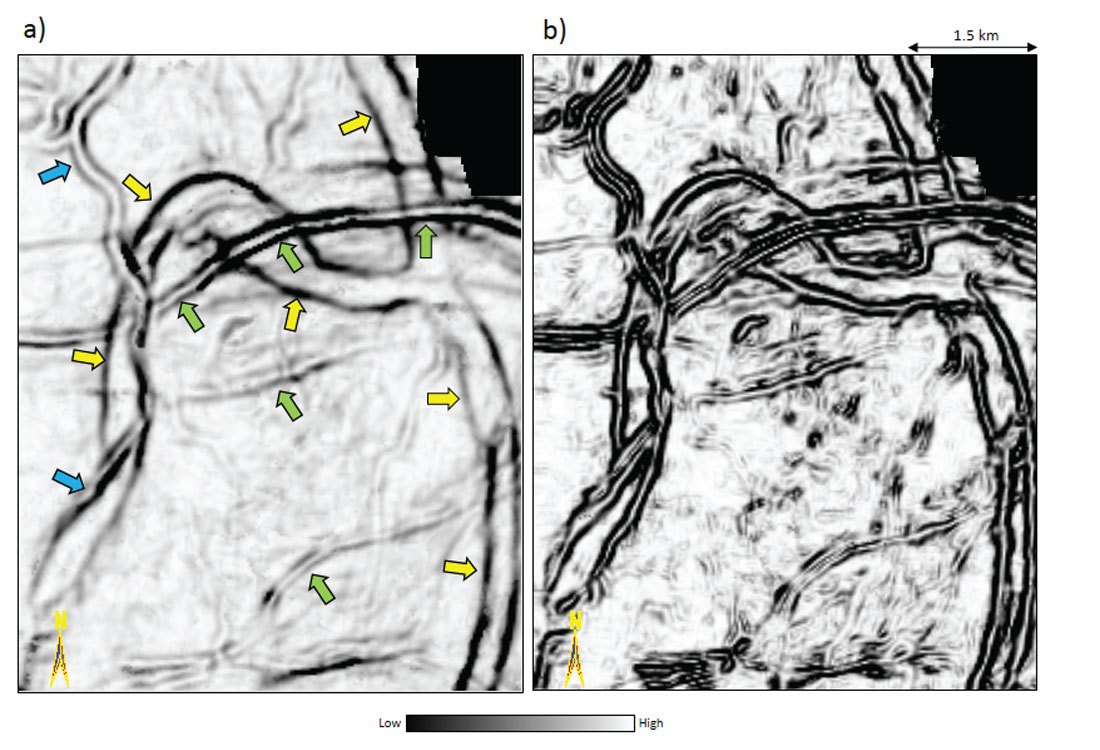
Such convincing displays suggest that the application of the Sobel filter to energy-ratio coherence used in the present exercise should help provide clear definition of many features of interest.

Automatic fault extraction software packages such as ant tracking operate on discontinuity volumes and provide an output volume consisting of fault planes. The quality of the results is dependent to a large extent on the quality of the discontinuity volume used. Needless to mention, a coherence volume with poorly-imaged features may not resolve the fault detail well. We suggest that coherence volumes sharpened by Sobel-filter application will provide improved input to such operations resulting in detailed, accurate fault plane surfaces.

Conclusions

Just as in photographic applications, the Sobel filter provides an excellent means of enhancing edges. Rather than apply the Sobel filter to the original seismic amplitude, we have applied it to coherence, resulting in sharpened images. The application of Sobel filters to coherence volumes enhances discontinuity features such as faults and channels, resulting in crisper, more focused images. We believe such images provide superior input to modern automated fault identification and object extraction software application as well as in visualizing the channel features clearly. Such applications would definitely help with the geologic understanding of the subsurface area of interest. A good and accurate extraction of the fault network system could serve as a useful input for geocellular modeling or for planning of potential drilling targets.

Similar applications with other discontinuity attributes could also be explored.

Acknowledgements

We wish to thank Arcis Seismic Solutions, TGS for encouraging this work and for permission to present these results. The authors extend sincere thanks to the Ministry of Oil, State of Kuwait and the Kuwait Oil Company for granting permission to publish this work.