Reflections from Contrasts in Isotropic Attenuative Media AVO and Beyond

The purpose of this article is to summarize and illustrate some features of new theory describing the interaction of seismic waves with viscoelastic structures and interfaces. Progress in these areas makes available more sophisticated tools for AVO analysis and inversion, and thereby quantitative interpretation, and for multi parameter full waveform inversion. The main theoretical step forward comes from determining the mathematical form of what is called the "scattering potential" for viscoelastic media.

A scattering potential is a mathematical object that describes how a wave interacts with a small point inclusion of matter in the subsurface. One imagines a tiny region of geology, with properties different from those surrounding it, being shaken by a seismic wave, whereupon it shakes in response, in a characteristic manner determined by its elastic properties. The scattering potential describes exactly how this happens. It arises from a fairly abstract, and some might feel esoteric, treatment of wave propagation in heterogeneous media, but it gives rise to two other quantities that are each so fundamental to modern seismic data analysis that taking the trouble to understand it is worthwhile. First, the scattering potentials are the sensitivity kernels used in full waveform inversion (FWI). Therefore, if a new FWI algorithm is sought to characterize a certain type of reservoir, the first stage is to lookup (or solve for) a suitable scattering potential. Second, the scattering potential is the generalization of amplitude variations with offset, and can easily be reduced to reproduce formulas for analysis of AVO. Stolt and Weglein (2012), for instance, show that the Aki-Richards equations are reproduced for small angles and small contrasts from the three-parameter elastic isotropic scattering potential. So, if a scattering potential suitable for a new or unusual elastic (or anelastic, etc.) parameterization is determined, the AVO equations appropriate for that parameterization are also immediately available. Expending effort analyzing and determining scattering potentials, in other words, is critical to extending the reach of modern seismic technology such as quantitative interpretation and full waveform inversion.

Anelasticity, or viscoelasticity, and its influence on seismic amplitudes and phases, affords a tantalizing link between seismic data and the properties of subsurface fluids and viscosities. Wave propagation in viscoelastic media have been treated by many authors both numerically and theoretically (e.g., Borcherdt, 2009; Krebes, 1983, 1984; Carcione, 1988, 1993). We consider having as complete a characterization as possible of viscoelastic scattering potentials – and therefore supporting quantitative interpretation and FWI – to be high on the list of research priorities for exploration and monitoring geophysics. Moradi and Innanen (2015a, 2015b, 2016) published some advances in this area regarding the scattering of homogeneous and inhomogeneous waves from inclusions in five viscoelastic parameters (density, P- and S-wave velocities, and P- and S-wave quality factors).

Here we will summarize the second of two applications of the viscoelastic scattering theory, namely, the extension it affords to AVO analysis, which is described in detail by Moradi and Innanen (2016), both as a special case of the more general scattering potential, and also as an approximate solution of the viscoelastic Zoeppritz equations.

These formulas are key elements of both linear and nonlinear viscoelastic AVO/AVF inversion procedures (e.g., Innanen, 2011; Bird, 2012), and quantitatively support a range of discussions about amplitude analysis from attenuating targets (Chapman et al., 2006; Odebeatu et al., 2006; Lines et al., 2008; Quintal et al., 2009; etc.). Let us briefly discuss the amplitude variation with offset of PP and PS viscoelastic waves at weak contrast interfaces in weakly attenuative isotropic media. The dependency of these approximate reflection coefficients on changes in both elastic and anelastic properties across the boundary are discussed. The consistency of the theoretical results with the numerically calculated synthetic data is examined.

Viscoelastic wave propagation

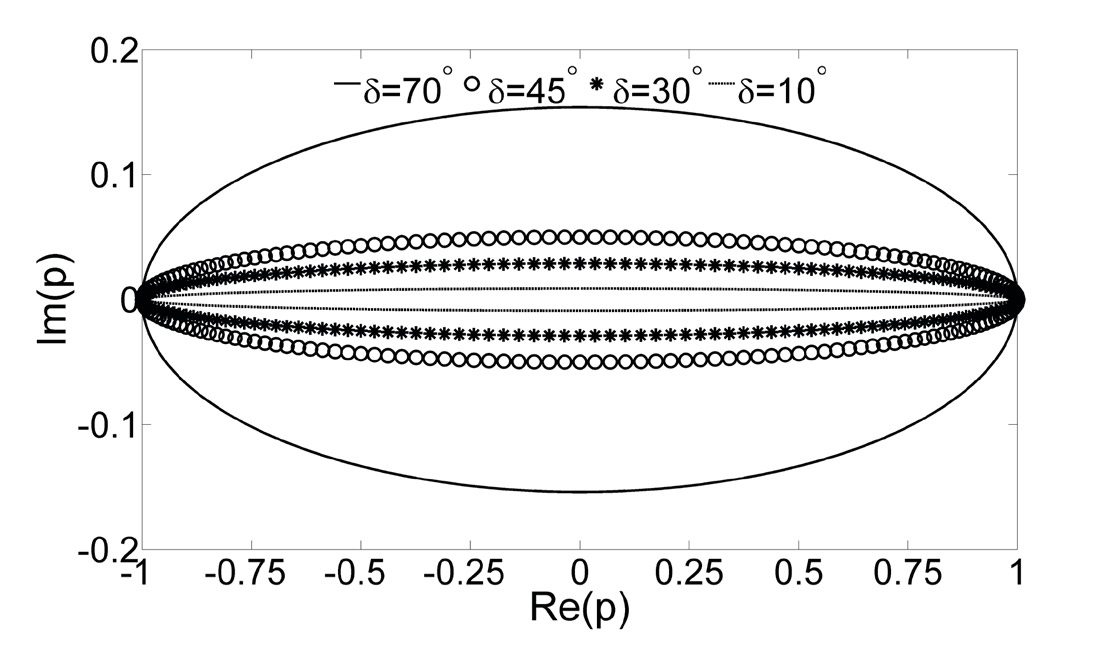
In an attenuative medium the wave number vector is complex, and given by K=P-iA, where P is the propagation vector, and A is the attenuation vector which characterizes the direction of maximum attenuation of the wave. If propagation and attenuation are in the same direction, the wave is called homogeneous; otherwise the wave is called inhomogeneous. The angle between these two vectors is referred to as the attenuation angle. Under this new, special, and complex wave number vector, three types of waves in an isotropic viscoelastic media can be found propagating: a P-wave and what is referred to as an SI-wave (Borcherdt, 2009), both with elliptical polarization, and a further wave, labelled SII, with linear polarization. The definition is such that, in the case that the attenuation goes to zero, SI- and SII-waves reduce to the standard elastic isotropic SV and SH waves with linearized polarizations. Figure 1 illustrates the nature of the complexity in the ray parameter and the effects on this parameter of a non-zero attenuation angle. It can be seen that the ray parameter describes an ellipse whose eccentricity grows for smaller values of attenuation angle, reducing to linear, as mentioned above, in the elastic limit. As we will discuss in next section, both the complex stiffness tensor and the complex polarizations resulting from this general picture make the reflection coefficients complex. In what follows we will denote the generalized SV wave (i.e., the SI-wave) by S, as our comments do not involve the other SII-wave mode.

Numerical viscoelastic amplitude variation with offset behaviour

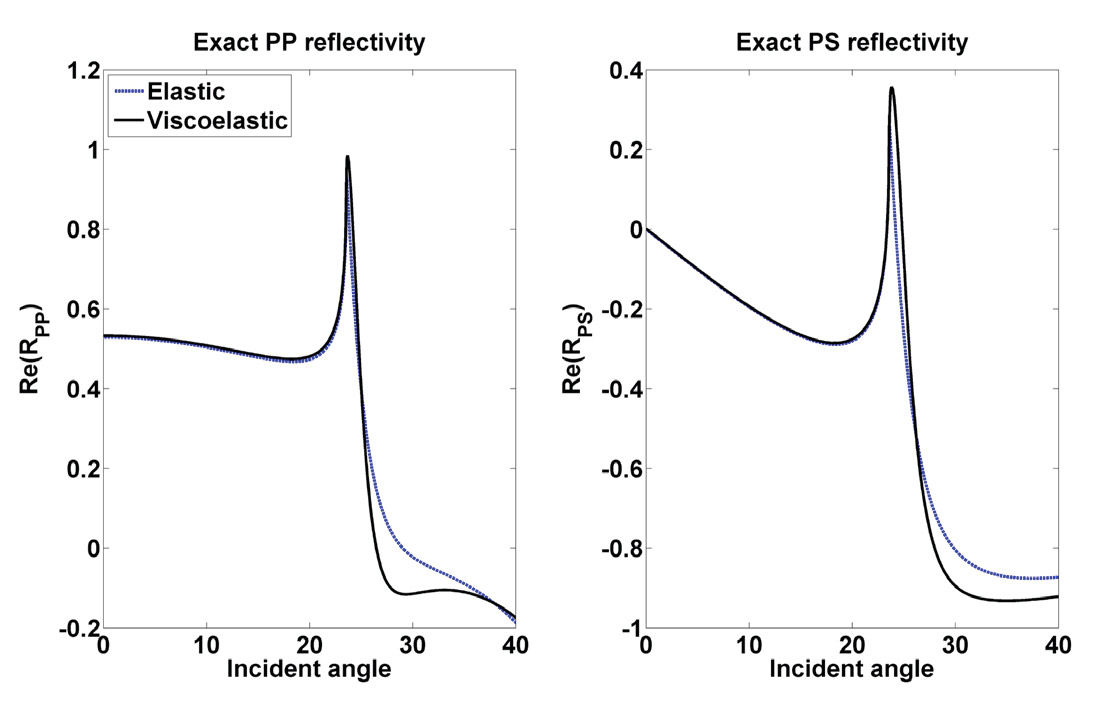
Let us illustrate some of the interesting features of the viscoelastic AVO problem graphically. We consider the reflection of an incident, inhomogeneous P-wave from a boundary separating two low loss viscoelastic media (i.e., where the Q_P and Q_S are much smaller that unity). It has been shown that an inhomogeneous P-wave can be reflected to become either an inhomogeneous P- or S-wave (Borcherdt, 2009). Generally these appear as second order effects, but in Figure 2, where we plot exact reflection coefficients in both elastic and viscoelastic media we can see significant deviations can occur at and beyond the critical angle. Precritical differences are visible also, however, and in cases where Q contrasts are large the viscoelasticity of the medium becomes a significant factor.

Qualitatively it is difficult to understand the sensitivity of the reflection coefficients to changes in properties across the interface when the exact Zoeppritz equations are used. However, if changes in elastic and anelastic properties between two layers are small, for incident angles smaller than critical we can linearize the exact reflection coefficients, either through direct manipulation of the Zoeppritz equations or through suitable simplification of the viscoelastic scattering potential. Let us list some of the conclusions available from inspection of the linearized forms, leaving the mathematical expressions for other venues (see Moradi and Innanen, 2016).

Reflected harmonic plane waves in viscoelastic media have complex coefficients. For P-to-P modes, we find that the real part of the linearized formulas are sensitive to changes in density, P-wave velocity and S-wave velocity. The imaginary part to first order appears only when non-negligible contributions come from the anelasticity of the medium. However, if significant anelasticity is present, this imaginary part is sensitive to changes in density, P- and S-wave velocities and P- and S-wave quality factors. In the limit where attenuation vanishes, elastic P-to-P reflectivity is recovered. We find that when there is no contrast in P- and S-wave quality factors, the imaginary part of the reflectivity is nevertheless not zero, but maintains a small imaginary part due to the attenuation in the background media. Similar explanations hold for the P-to-S mode. Perhaps not surprisingly, the P-to-S mode is to first order insensitive to changes in P-wave velocity and P-wave quality factor. In fact, while changes in the S-wave quality factor affect all of the P-to-P, P-to-S and S-to-S modes, changes in the P-wave quality factor only affect the P-to-P mode.

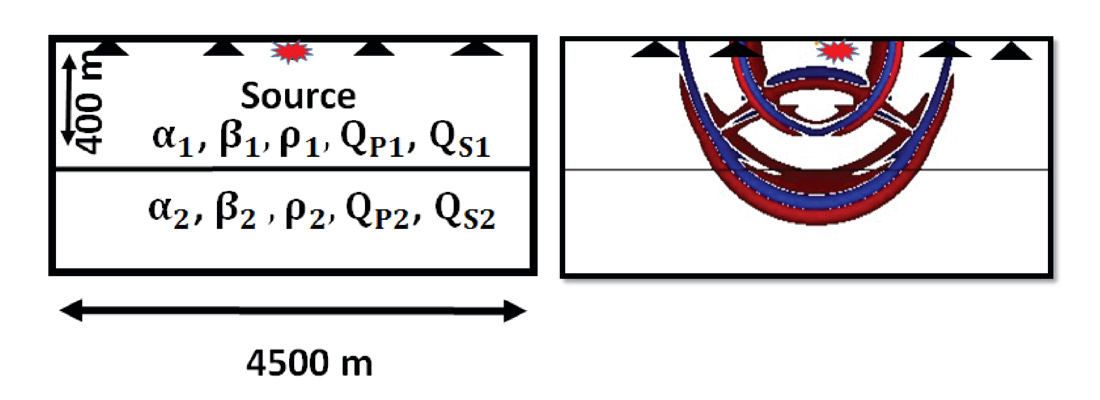
Let us finally square some of these results of AVO theory with what we see in finite difference modelling of viscoelastic wave propagation. Here we used the code developed by Martin and Komatitsch (2009) to simulate the reflections caused by general viscoelastic contrasts. We will examine the contributions of changes in quality factors across a single viscoelastic boundary to the amplitudes of backscattered waves. In Figure 3 the geometry of the Earth model is illustrated in the left panel; in the right panel a snapshot of the viscoelastic wave field during propagation is illustrated. The Earth model is a simple two layer structure, embedded in a 900×200 grid with spacing Δx = Δy = 5m. We put the layer boundary at a depth of 400m to set up contrasts in elastic and anelastic properties. To make a clean input wave the source was buried at depth 50m and consisted of a vertical displacement injected with a wavelet with a central frequency of 45Hz.

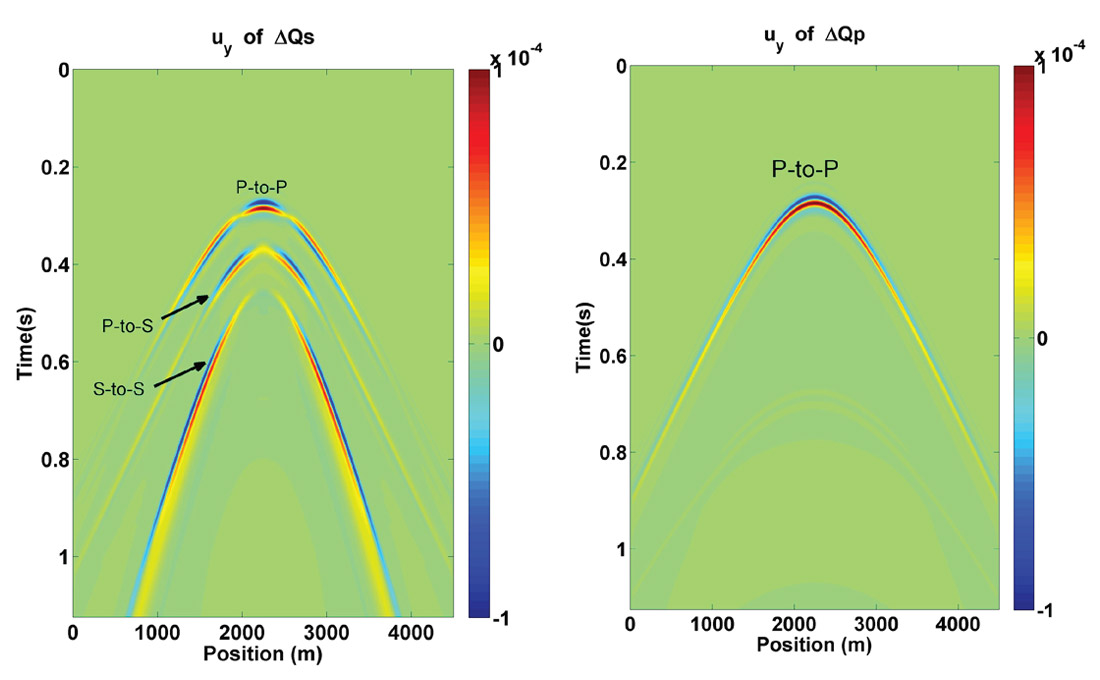
In Figure 4 we consider new snapshots, but those coming from interfaces across which a more selective set of parameter contrasts have been set up. In Figure 4a, the x-component of displacement is plotted for an interface involving a change in the S-wave quality factor only. As we can see, this leads to the existence of P-to-P, P-to-S and S-to-S modes, as predicted by the linear equations. Figure 4b is a plot of the same displacement calculated for an interface involving a contrast in the P-wave quality factor only. Here we confirm that a change in the P-wave quality factor only generates one P-to-P reflection mode.

Summary

We seek to supply elements needed for both AVO theory and FWI sensitivities, tuned so as to accommodate as complete as possible a model of viscoelastic wave propagation. This will therefore increase our ability to characterize partially saturated reservoirs, and fluids with and without viscosity variations. We have reviewed and illustrated the effects of anelasticity on the reflection of waves from a boundary between two viscoelastic media. We consider the incident wave to be inhomogeneous, and both media to support low-loss attenuation. Additionally, we assume that the contrasts between the properties of the upper and lower media are weak. Though not discussed here, it is interesting to note that to derive the linearized reflectivity, incorporating a proper complex Snell’s law is extremely important, as it is used to express the transmitted phase angle and attenuation angle in terms of the incident phase and attenuation angles. It is interesting that even in absence of changes in quality factors, reflection coefficient contributions arising from the anelasticity are not zero. In the case that attenuation in both media goes to zero, the imaginary part of the reflectivity vanishes and the standard elastic isotropic Aki & Richards approximation is recovered.