Abstract
Two petrophysical models for cracked media are investigated in this paper: the Kuster-Toksöz (1974) model for randomly oriented cracks and Hudson’s (1981) model for aligned cracks. We consider the effects of crack shape, aspect ratio, and crack density using rock properties from several field locations: the Ross Lake heavy oil field, Saskatchewan; the Violet Grove, Alberta CO2 injection site; and a Saskatchewan mining area. Generally, introducing cracks or inclusions into a rock can significantly decrease its P- and S-wave velocities. Inclusion shape has a large influence on the resultant rock properties from the Kuster-Toksöz model. Small aspect ratios (thinner cracks) can yield the largest decreases in velocities. Modeling results indicate that a 1% porosity, from pennyshaped cracks with an aspect ratio of 0.01, can produce up to 22% velocity decreases in Hudson’s model. Similar inclusions create P-velocity decreases of 16% and S-velocity decreases of 11% in the Kuster-Toksöz model.
Introduction
The Kuster and Toksöz (1974) method calculates the effective moduli for randomly distributed inclusions in a rock based on a long-wavelength, first-order scattering theory. The overall effect of the inclusions is isotropic. The Hudson (1981) model uses scattering of the mean wavefield in an elastic solid with thin, penny-shaped cracks or inclusions which are aligned in a specific direction. The effective moduli can be calculated by applying first- and second-order corrections to the isotropic background moduli. The overall effect of the aligned cracks is anisotropic.
Both models assume no fluid flow between spaces, thus they simulate high-frequency, saturated-rock behavior. At low frequencies, when there is time for wave-induced pore pressure increments to flow and equilibrate, dry-rock moduli should first be calculated from the two models. Then Gassmann fluid substitution for isotropic media and Brown and Korringa’s (1975) fluid substitution for anisotropic media could be used to predict saturated rock properties.
Rock properties for numerical test
Several rock types are selected to provide values for numerical tests: a Cretaceous-aged, high-porosity (about 30%) channel sand and a tight sand from the Ross Lake heavy oil field, another Cretaceous-aged low-porosity (about 12%) sandstone from Violet Grove, Alberta, and a Devonian carbonate and a shale from a potash mining area in Saskatchewan. These rock properties are listed in Table 1. The porous channel sand and tight sand from the Ross Lake area were used for various parameter tests with the Kuster-Toksöz model and Hudson’s model. For this modeling, the Hashin-Shtrikman bounds were also calculated for comparison. The Hashin-Shtrikman bounds are the narrowest constraints when the geometries of the constituents are not known. Cracked rock properties are also calculated for all the chosen rocks assuming penny-shaped cracks - with a fractional crack porosity of 0.01 and an aspect ratio 0.01. For all the tests, the void spaces are filled with brine at a density of 1.1 g/cm3 and velocity of 1430 m/s.
| Ross Lake | Violet Grove | Sask. Mining | |||
|---|---|---|---|---|---|
| Table 1. Rock properties for numerical tests of cracked media. | |||||
| Lithology | Sandstone | Sandstone | Sandstone | Carbonate | Shale |
| Depth | 1148m | 1160m | 1605m | 970m | 1006m |
| Vp (m/s) | 3026 | 5689 | 3778 | 5538 | 3765 |
| Vs (m/s) | 1721 | 3413 | 2237 | 2954 | 2074 |
| Density (g/cc) | 2.133 | 2.63 | 2.42 | 2695 | 2326 |
| Porosity | 30% | 2% | 12% | 3% | <5% |
Kuster-Toksöz Model
Figures 1a and 2 display the results of randomly oriented inclusions in the porous channel sand of the Ross Lake heavy oil field as calculated by the Kuster-Toksöz model. Dry moduli were calculated first by supposing that both bulk and shear moduli of the inclusions are 0, then the Gassmann equation was used to calculate the effective moduli when the void space is filled by brine. As shown in Figure 1a, we find that the velocities decrease significantly, depending on the inclusion shape. Smaller aspect ratios yield a larger decrease of velocities. The velocities of the sphere inclusion shape are coincident with the Hashin-Shtrikman upper bound. The sphere inclusion shapes give the same results from the Kuster-Toksöz (1974) formula and a generalized formula (Berryman, 1980). The effective velocities of the small aspect ratio shapes approach the Hashin-Shtrikman lower bound at a smaller volume fraction of pores. Except for the sphereshaped inclusions, all other inclusion shapes have a limitation on volume fraction values for reasonable effective velocity values. The concentration value limitations decrease with aspect ratio. For needle shaped inclusions, there is no dependence on aspect ratio. The results are valid for a large range of concentration values.
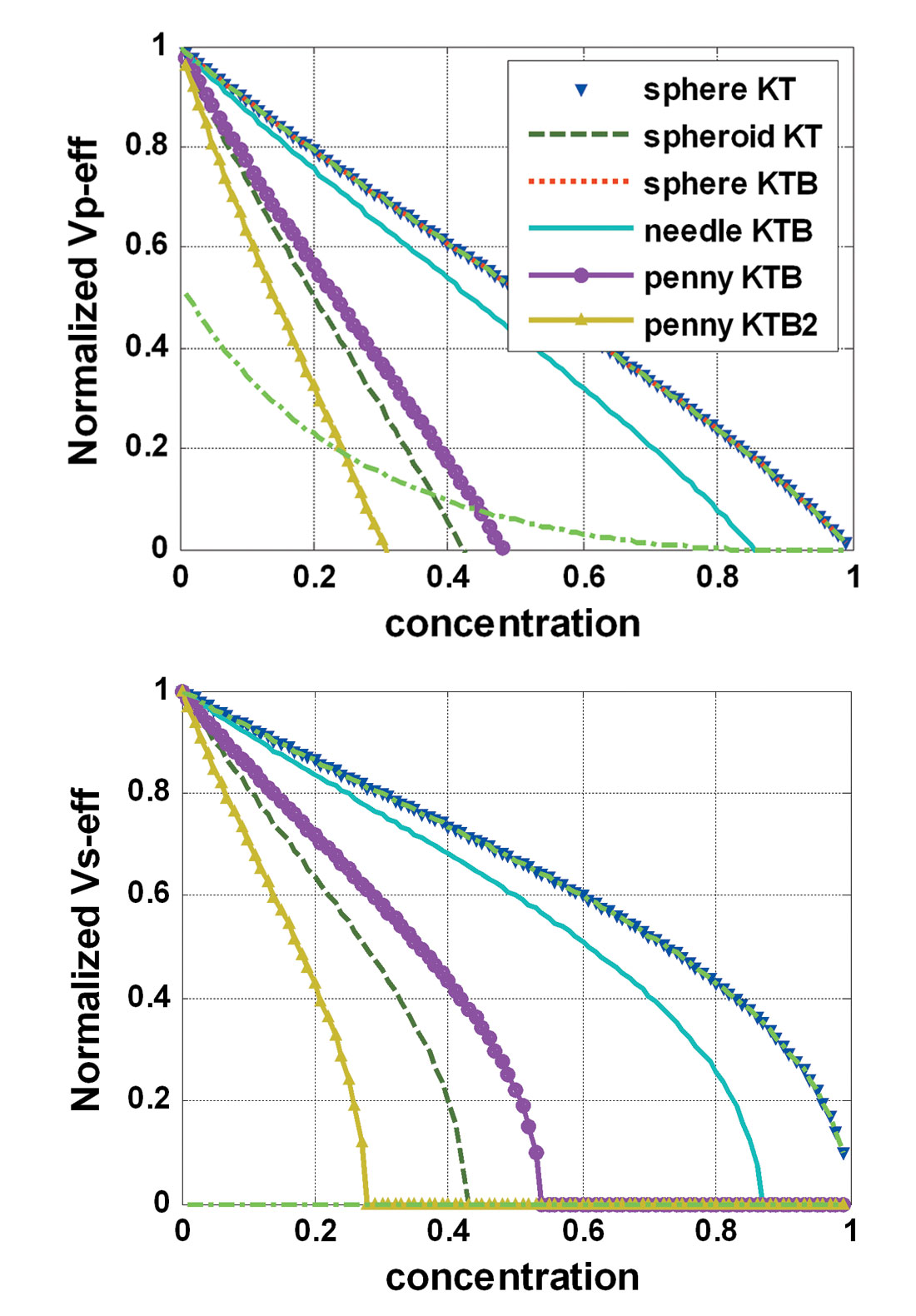
The same calculation was carried out for the tight sand of the Ross Lake heavy oil field (Figure 1b). The concentration limitations for each inclusion shape are quite similar to those of the porous sand.

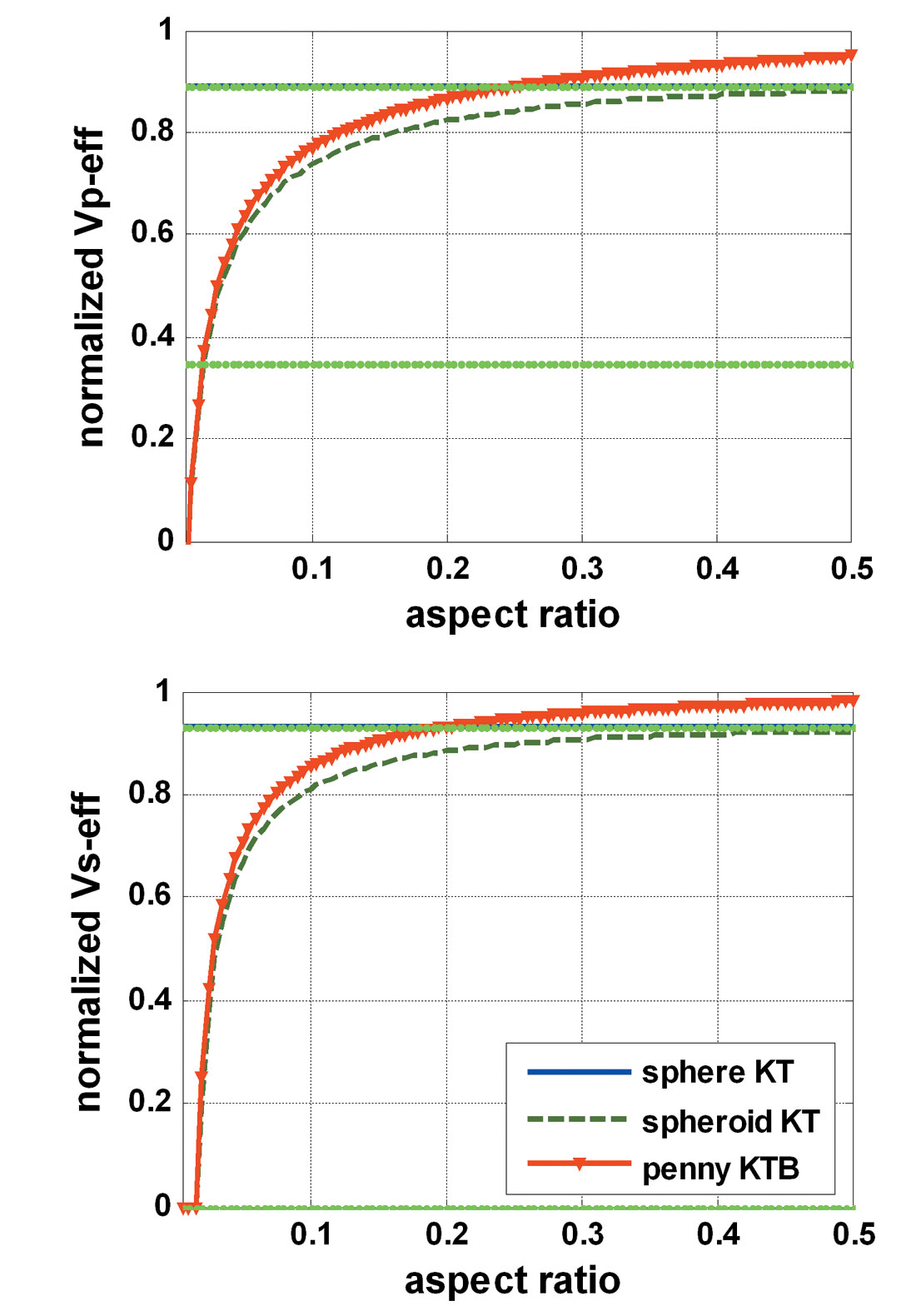
Figure 2 shows the variation of effective velocities with aspect ratio α for spheroid and penny shaped pore. The volume fraction c of the pores was set to be 0.1. When the aspect ratio is too small, the assumption of no fluid flow cannot be satisfied, thus the model cannot give reasonable results. When the aspect ratio increases, velocity drops will decrease. The results of spheroid shapes will approach those of the sphere. For penny shapes, the aspect ratio cannot be too large; otherwise, the predicted velocities will exceed the upper bound.
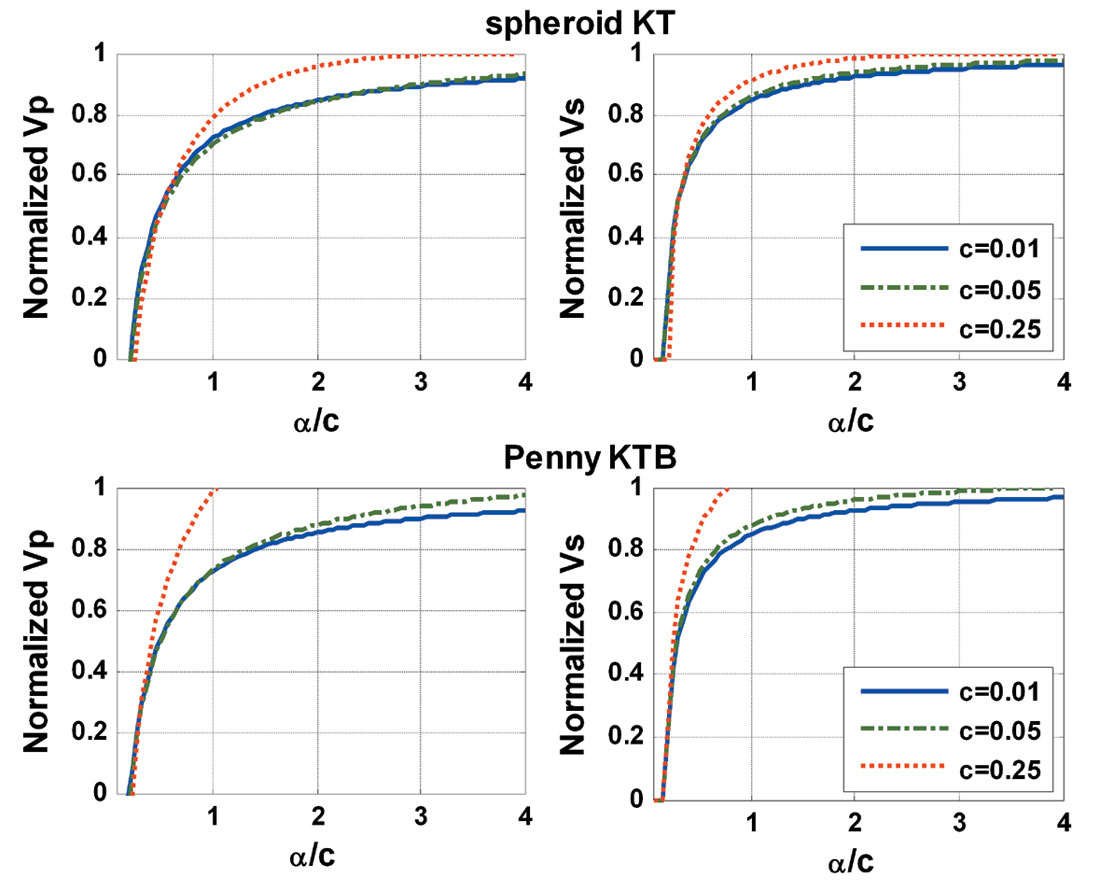
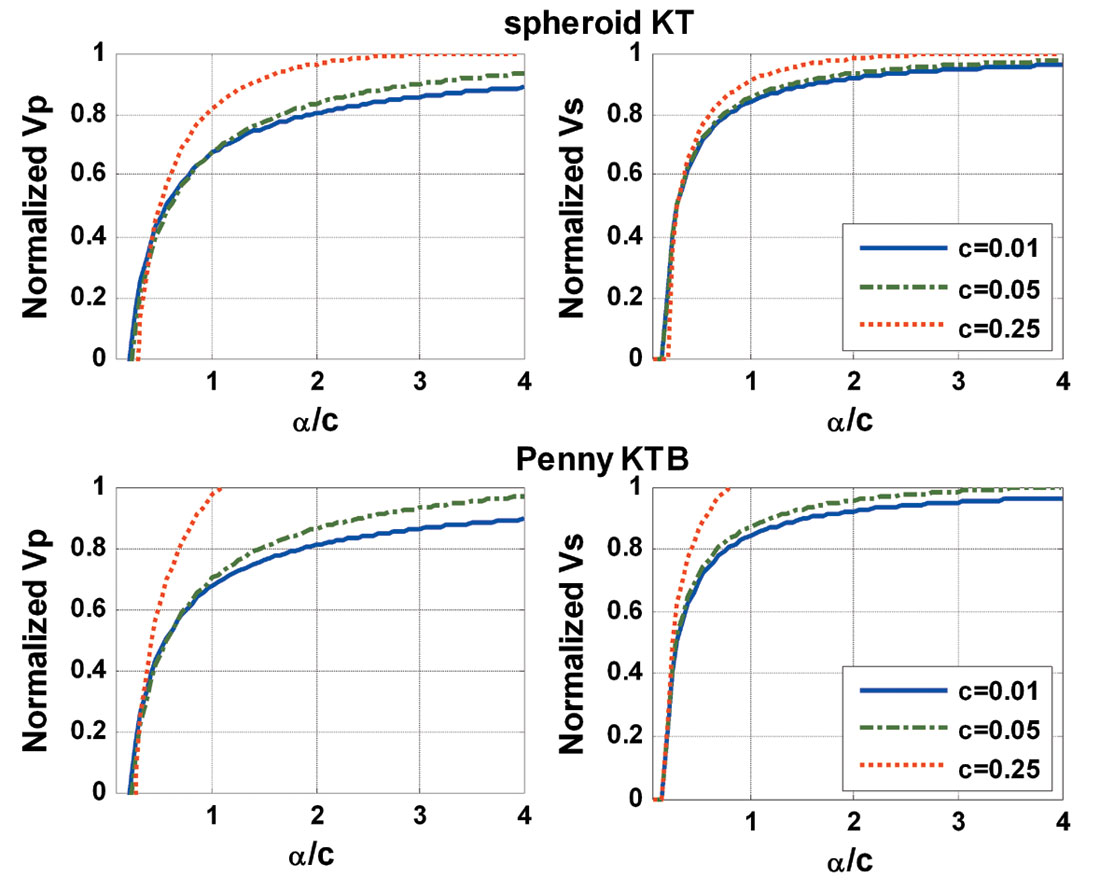
From the results displayed in Figure 2, the α/c value should be within some range so that the predicted velocities fall within the Hashin-Shtrikman bound. To investigate the range, a test of the α/c value with different c values (0.01, 0.05, and 0.25) was carried out and the results are shown in Figure 3a for the Ross Lake porous channel sand. The velocity values in Figure 3a were normalized by the Hashin-Shtrikman upper and lower bound. For various c values, both P- and S-velocities indicate relatively stable minimum α/c values, approximately 0.2 (0.4 from moduli calculation results). However, for penny-shaped inclusions, the maximum α/c values for reasonable velocities change drastically with respect to the crack concentration value c. Small c values will still have reasonable effective velocities for large α/c values. The P-velocities have less limitations on the α/c values than S-velocities. For spheroid inclusions, there is no upper limitation on the α/c value, but with increasing c value, the effective velocities approach the upper bound quickly. From the calculation carried out on tight sands of the Ross Lake heavy oil field (Figure 3b), a similar conclusion can be made.
Hudson’s model
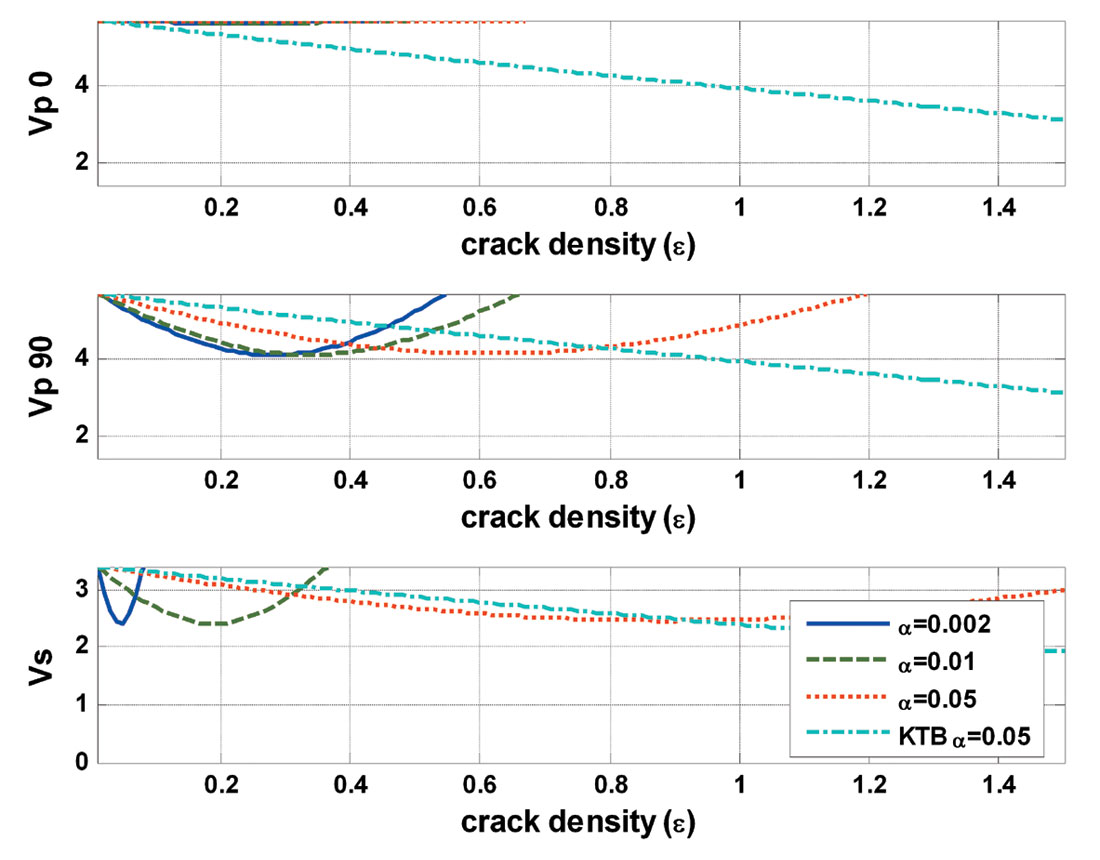
Figure 4a shows the results of the Ross Lake porous channel sand from Hudson’s model for penny cracks with three aspect ratios (α): 0.002, 0.01, and 0.05. It displays the modeled P- and S-velocity variations with crack density. When the rock contains aligned cracks, it will display anisotropy. For the cracks aligned in one direction, it will show transverse anisotropy with respect to the axis along the normal to the cracks. The P-velocity drops very little when the waves travel along the crack plane, but will display a distinct decrease when the wave travels normally to the cracks. For SV waves, the velocity will change the same amount whether it travels normal to the cracks or across the crack plane. Cracks with aspect ratio 0.05 were also modeled by the Kuster-Toksöz model for penny-shaped cracks. The effective P-velocities from the Kuster-Toksöz model are between the P-velocities from Hudson’s model along the crack normal and crack plane.
For cracks with a given aspect ratio, when the crack density exceeds a limit, the velocities will display an abnormal increase with crack density value, especially for Vs. This limit is about 0.05 (a 0.1% crack porosity equivalent) for cracks with aspect ratio 0.002 and 0.2 (around 1% crack porosity) for cracks with aspect ratio 0.01.
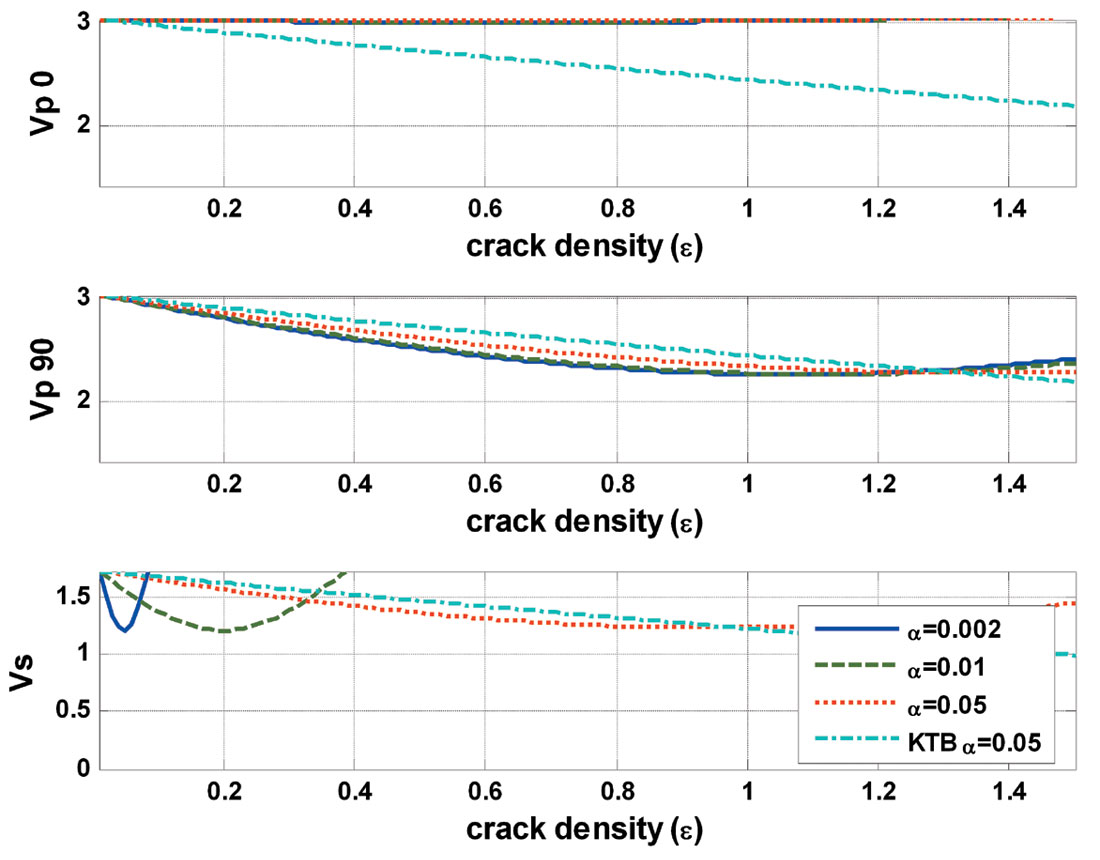
From the modeling results for tight sand from the Ross Lake area (Figure 4b), we find that the P-velocity variations with crack density show an apparent dependence on rock properties of the uncracked rock, while the S-velocity displays a similar variation with crack density. However, reasonable crack density ranges for each aspect ratio are still the same due to the similar variation of S-velocity with crack density.
Assuming a 1% crack porosity induced by penny-shaped cracks with aspect ratio 0.01, the effective P- and S-velocities from Kuster-Toksöz and Hudson’s model are plotted in Figure 5 for: 1) the Ross Lake porous sand, 2) Saskatchewan mining shale, 3) Violet Grove sand, 4) Saskatchewan mining carbonate and 5) Ross Lake tight sand. We find:
- 1. These cracks can produce up to 22% velocity decreases in Hudson’s model, and P-velocity decreases of 16% and S-velocity decreases of 11% in the Kuster-Toksöz model;
- The percentage changes of S-velocity induced by the cracks are quite similar for each rock from both models;
- The percentage changes of P-velocity along crack planes are very similar from Hudson’s method with or without fluid substitution;
- The percentage changes of P-velocity (P-velocity along the crack normal for Hudson’s model results) are consistent with the values of uncracked rocks from Kuster-Toksöz model and Hudson’s method without fluid substitution.

Conclusions
Two petrophysical models (from Kuster-Toksöz and Hudson) for cracked media are discussed. With given assumptions, the Kuster-Toksöz and Hudson’s methods can predict rock properties within the Hashin-Shtrikman bounds for randomly oriented cracks and aligned cracks, respectively.
From the results of the Kuster-Toksöz model, we find that the changes in rock properties depend largely on the inclusion shape. For both spheroid- and penny-shaped inclusions, α/c values should not be smaller than about 0.4 (equivalent to c<2.5α). For penny-shaped inclusions, the valid maximum α/c values change drastically with respect to the concentration value c. For Hudson’s model, smaller aspect ratio cracks have a smaller valid crack density range, especially for Vs.
The modeling results for several rocks (assuming 1% crack porosity, 0.01 aspect ratio penny-shaped cracks) indicate: the percentage changes of S-velocity from both models and P-velocity along crack planes from Hudson’s method have almost no dependence on uncracked rock properties; while the percentage changes of P-velocity (P-velocity along the crack normal for Hudson’s model results) are consistent with the values of uncracked rocks for the Kuster-Toksöz model and Hudson’s method without fluid substitution.











Join the Conversation
Interested in starting, or contributing to a conversation about an article or issue of the RECORDER? Join our CSEG LinkedIn Group.
Share This Article