Leakage of the Indian Ocean Tsunami Energy into the Atlantic and Pacific Ocean

Abstract

The tsunami of 26 December 2004 in the Indian Ocean propagated not only throughout the Indian Ocean but also propagated into the Pacific and Atlantic oceans. Some of the tsunami energy from the Indian Ocean leaked into the Pacific and Atlantic oceans through the opening in the south. This leakage of tsunami energy from the Indian Ocean produced maximum tsunami amplitudes of 0.65 m on the Pacific coast of South America, and maximum amplitude of 0.3 m on the coast of Nova Scotia in the Atlantic Ocean. A simple analytical model has been adapted here to show that indeed the tsunami flux from the Indian Ocean into the Pacific Ocean is greater than the flux into the Atlantic Ocean.

1. Introduction

Of the four oceans on the globe (Figure 1), the Pacific, Atlantic and Indian oceans are all connected in the south, through what is generally referred to as the Southern Ocean. The Atlantic and Pacific oceans are connected in the North to the Arctic Ocean. The Indian Ocean is not connected to the Arctic Ocean, at least directly.

For convenience, one can define a global tsunami as one that not only propagates throughout the ocean in which it is generated, but also into at least two other oceans, but need not necessarily cause loss of life and/or damage in these two other oceans. The Indian Ocean tsunami of 26 December 2004 was a global tsunami in this sense.

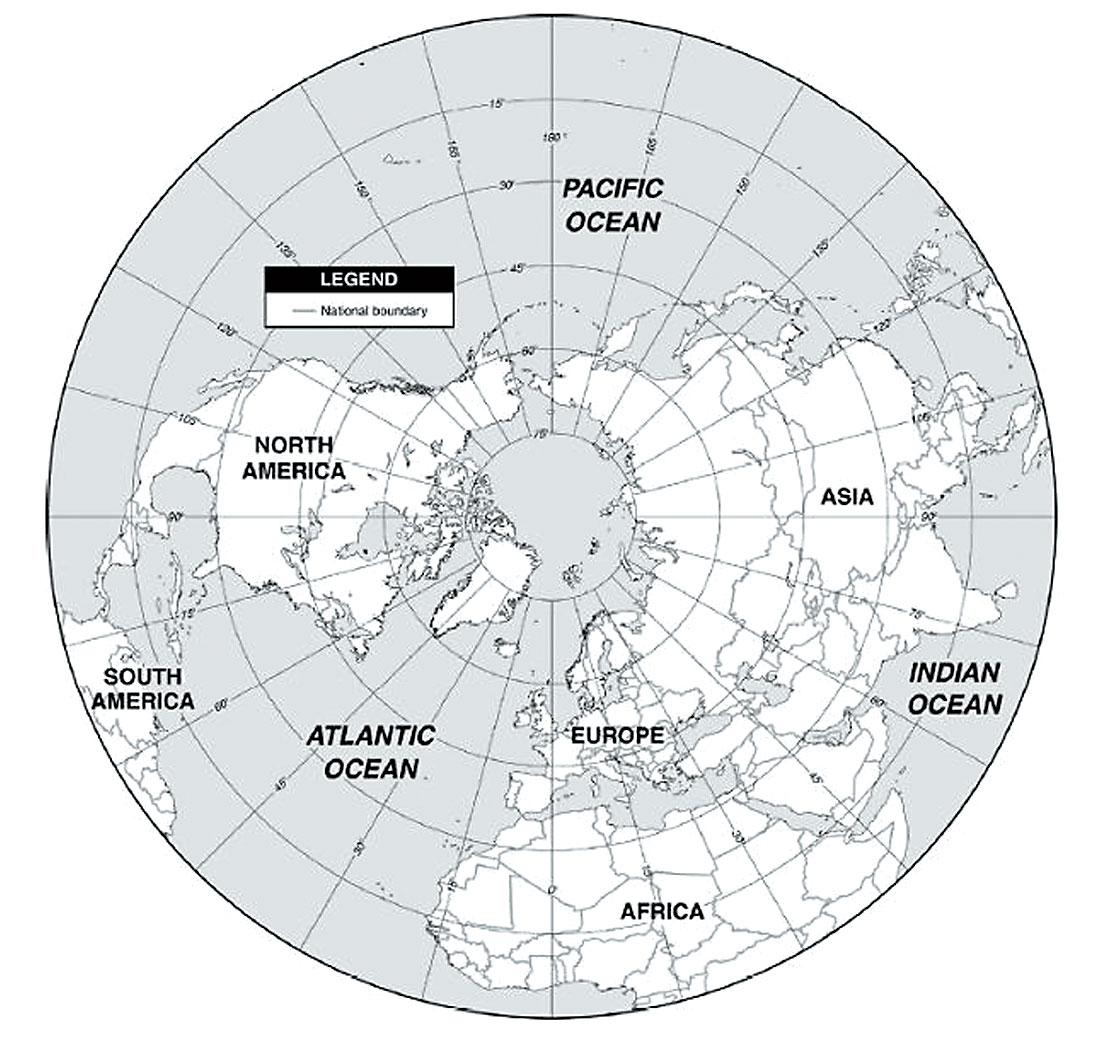
For convenience, one can define a global tsunami as one that not only propagates throughout the ocean in which it is generated, but also into at least two other oceans, but need not necessarily cause loss of life and/or damage in these two other oceans. The Indian Ocean tsunami of 26 December 2004 was a global tsunami in this sense.

According to the numerical model of Kowalik et al (2005) and also supported by an analysis of the observed tide gauge records (Rabinovich, 2005), the maximum tsunami amplitudes of up to 0.65 m occurred in the Pacific Ocean, on the pacific coast of South America, while maximum amplitude of 0.3 m occurred in the Atlantic Ocean on the coast of Nova Scotia, Canada. One can ask the question, why the tsunami amplitudes in the Pacific Ocean are more than twice those in the Atlantic Ocean. In other words, why much greater tsunami energy was leaked into the Pacific Ocean from the Indian Ocean than into the Atlantic Ocean. The answer to this question depends to some degree on the directivity of tsunami energy. The main reason for a greater tsunami energy flux into the Pacific Ocean than into the Atlantic Ocean is the much shorter travel distance for the tsunami from the epicentre area to the opening or window between the Indian Ocean and the Pacific Ocean. The window between the Indian and the Pacific oceans is the gap between Australia and Antarctica, while the window between the Indian and Atlantic oceans is the gap between South Africa and Antarctica. These two gaps are roughly comparable in the width, with the Atlantic gap being slightly larger. However, the travel distance from the epicentre to the Atlantic gap is much greater than the travel distance from the epicentre to the Pacific gap.

In the following sections, Section 2 presents some observational data and Section 3 discusses a simple analytical model that is adapted to account for the leakage of tsunami energy.

2. Observational Data on Leakage of Tsunami Energy

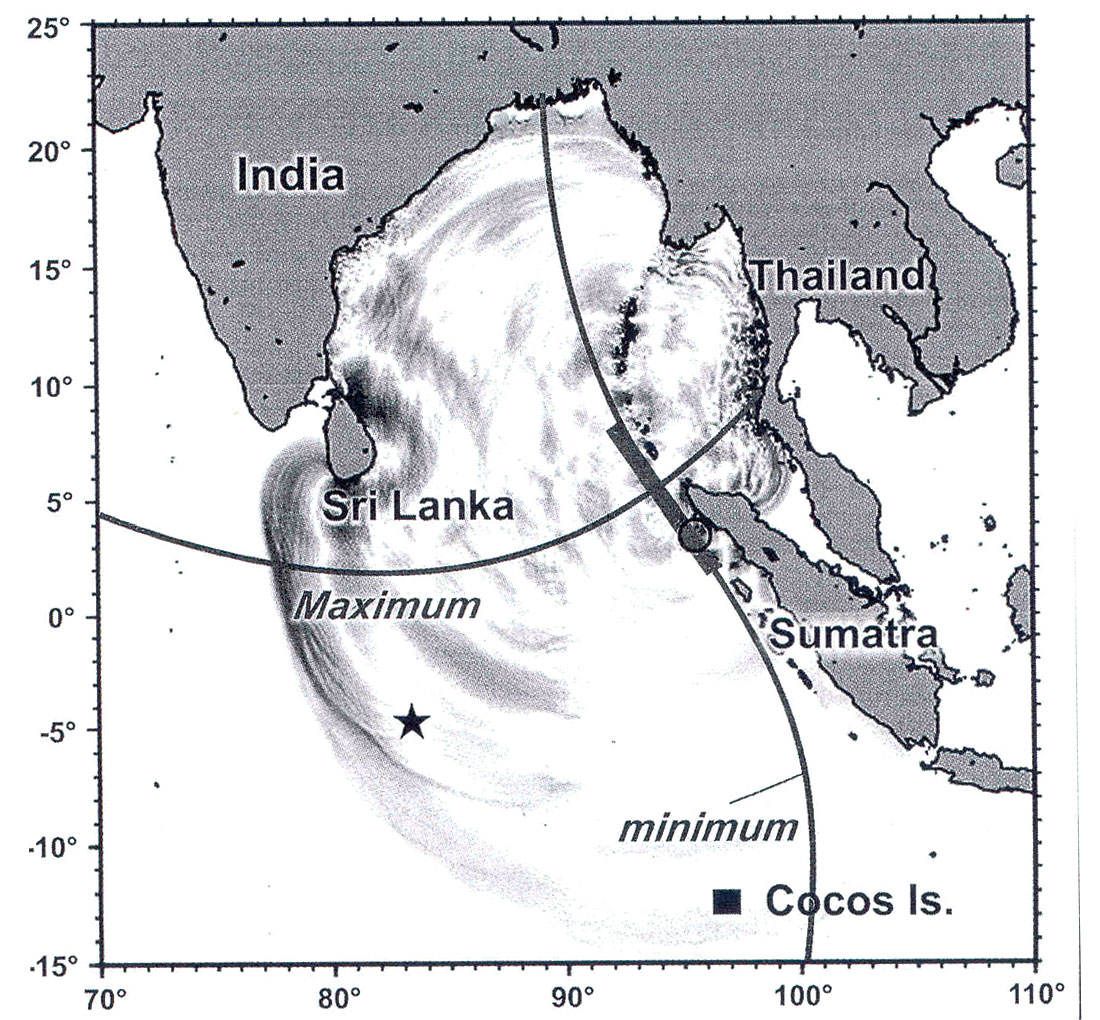
Figure 2 shows the main direction of tsunami energy flux. Table 1 lists various tsunami parameters. It is the second wave of the tsunami that has greatest amplitudes in all the three oceans. Figure 3 shows the amplitudes of the tsunami at various locations in the Pacific Ocean.

3. Adaptation of A Simple Analytical Model

Munk (1963) computed the leakage of tsunami energy from the Pacific Ocean into the Atlantic and Indian oceans, making use of a very simple analytical model which borrows the concept of a leakage of energy from acoustics. We adapted Munk’s model here, with a slight revision in the sense that here the leakage of tsunami energy is from the Indian Ocean into the Pacific and Atlantic oceans.

Figure 4 shows schematically the main paths for the leakage of tsunami energy. Kowalik et al. (2005) point out that the tsunami energy fluxes into the Pacific Ocean from the Indian Ocean, through the Indonesian straits is not significant. Munk (1963) introduced several useful concepts for tsunami dissipation (in analogy with acoustics). A typical e-folding time (i.e. time taken for the initial intensity to decay to 1/e of its value) for tsunamis is 1⁄2 day and a typical reverberation time is of the order of a week. (When a pistol is fired in an empty hall the sound echoes and reechoes from the walls, ceilings, and floors for a considerable time. Acoustical engineers call this phenomenon ‘reverberation time’). For Pacific Ocean tsunamis, he also considered the leakage of energy into the Atlantic and Indian oceans.

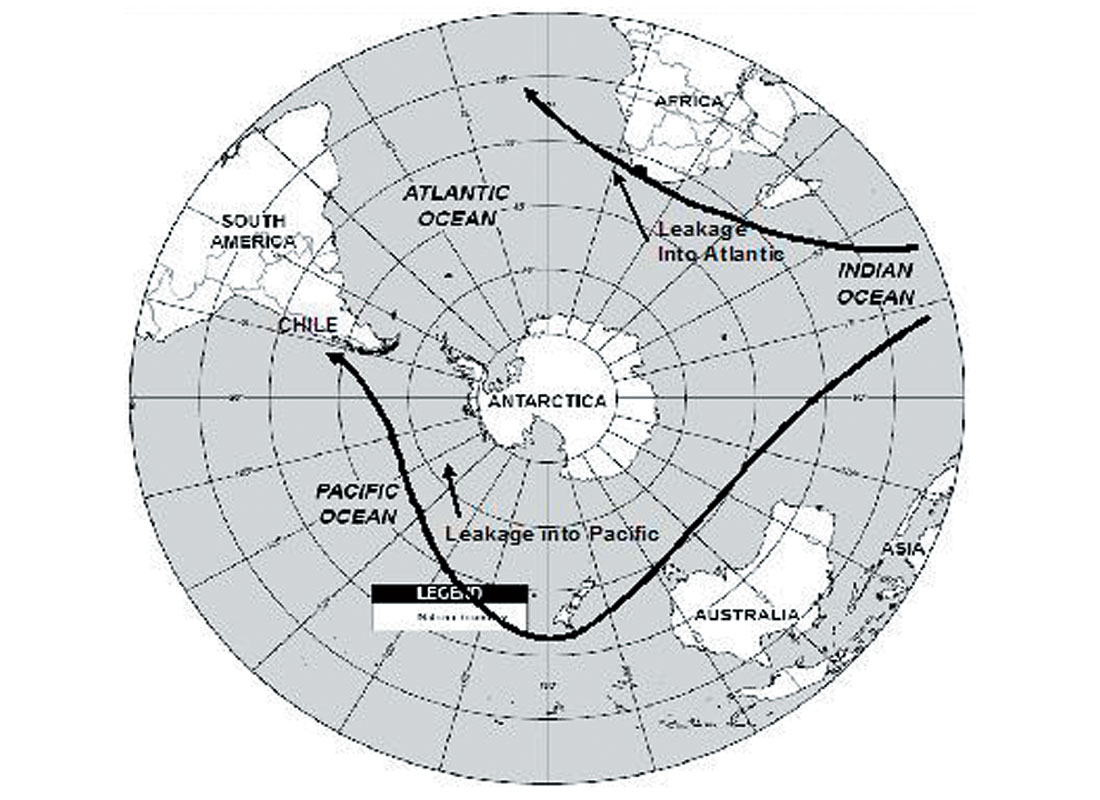
Munk estimated the circumference of the Pacific Ocean to be 45,000 km, not including the Antarctic windows of 3500 km. To estimate the circumference, all irregularities of the coastline shorter than a wavelength were ignored. From this information, he estimated that roughly 1.7 reflections per day could occur in the Pacific Ocean.

Munk concluded that the duration of the tsunami would not be significantly affected by dispersion from the following arguments. First, he wrote:

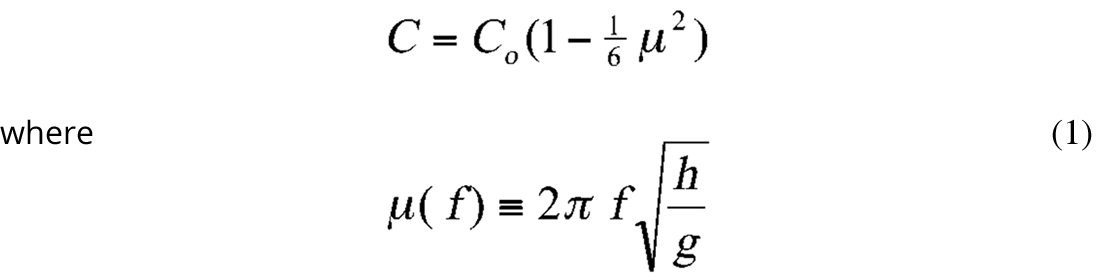
is the velocity at zero frequency and C(ƒ) is the velocity at frequency ƒ. As most tsunami energy is contained in frequencies less than 12 cycles/h, ƒ = 1/300 cycles per sec (cps). Also, taking an average depth of 4 km for the Pacific Ocean, μ ≈ 0.4 and C/C° ≈ 0.097 and are obtained. Thus the dispersive delay of high frequencies is about 3% and according to Munk, even for the most distant source the duration of the direct wave would not increase by more than 1 h, and even after 5 days of multiple reflection and scattering, the dispersive lengthening is only by as much as 4 h.

To determine the leakage of energy from the Pacific Ocean, Munk assumed a highly idealized model, where he ignored variations of intensity in a given ocean. Let I_i ( i = 1, 2, 3) be the intensities of the tsunami of the Pacific, Atlantic, and Indian oceans and S_i be the surface areas. The flux of energy from the Pacific Ocean into the Atlantic is:

(I₁ – I₂) C R₁₂

where R₁₂ is the width of the opening between the oceans. There are three equations of the following form, one for each ocean:

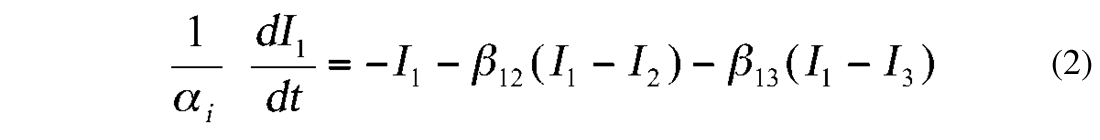
where α_i (i = 1, 2, 3) are constants to be determined and β_ij are defined:

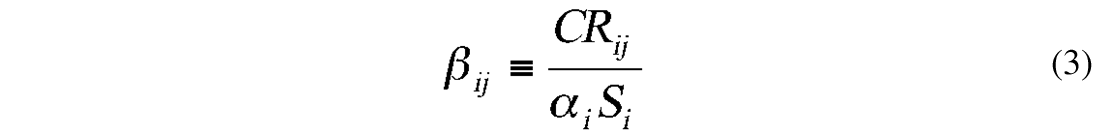
The other two equations can be written simply by a cyclic rotation of the subscripts, noting that β_ij β_ji

Next, Munk assumed that the energy decayed by a factor 1/e for each reflection for the three oceans. He gave for α_i

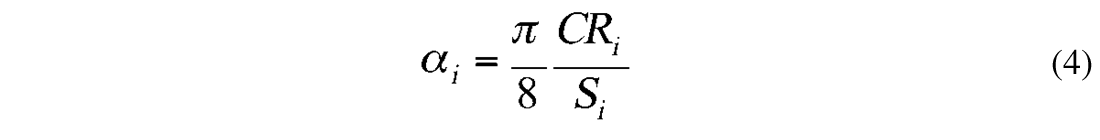
where R_i are the circumferences of these oceans. The leakage coefficients are then given by:

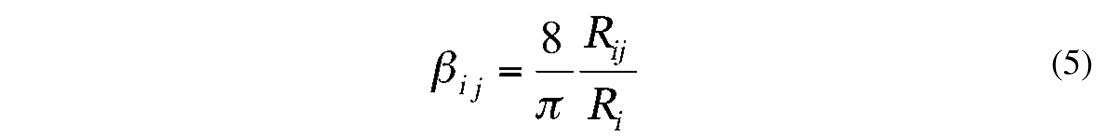
which shows that these depend only on the fractional length of the openings or windows.

The solutions for the intensities can be written as:

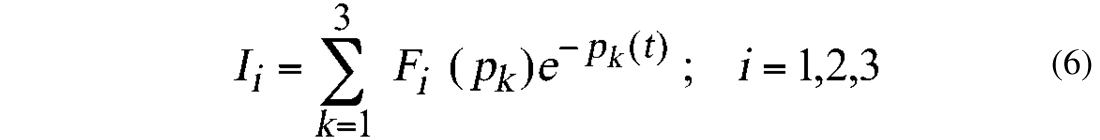
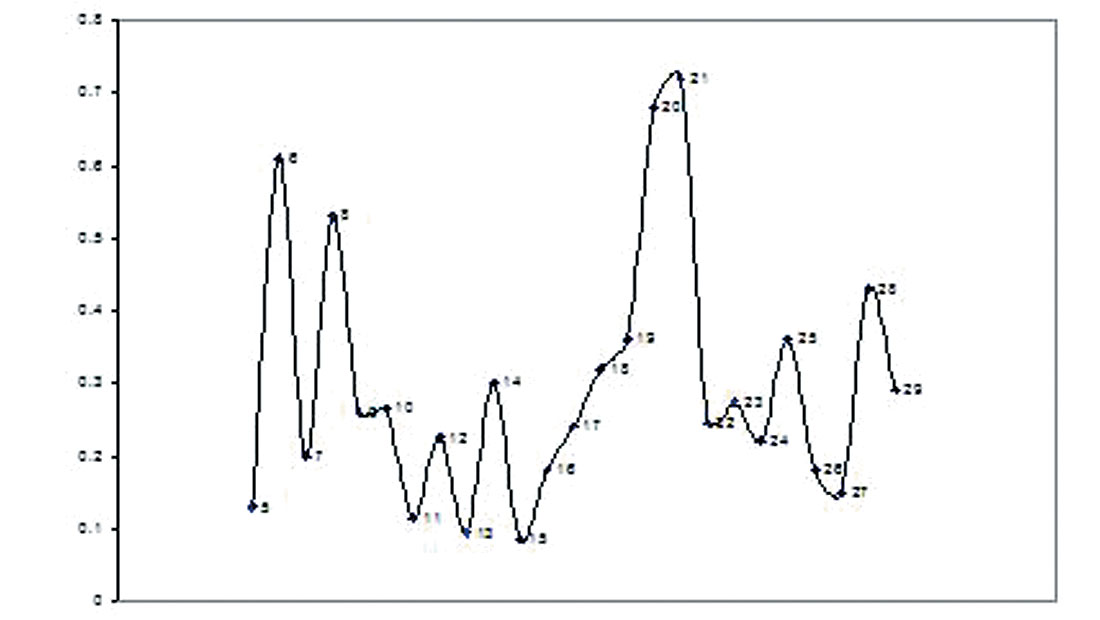
knowing α_i and β_ij, the roots, Ρ_k , and the coefficients, F_i (Ρ_k ), can be evaluated. Figure 5 shows the decay of the normalized intensities for the Pacific, Atlantic, and Indian oceans.

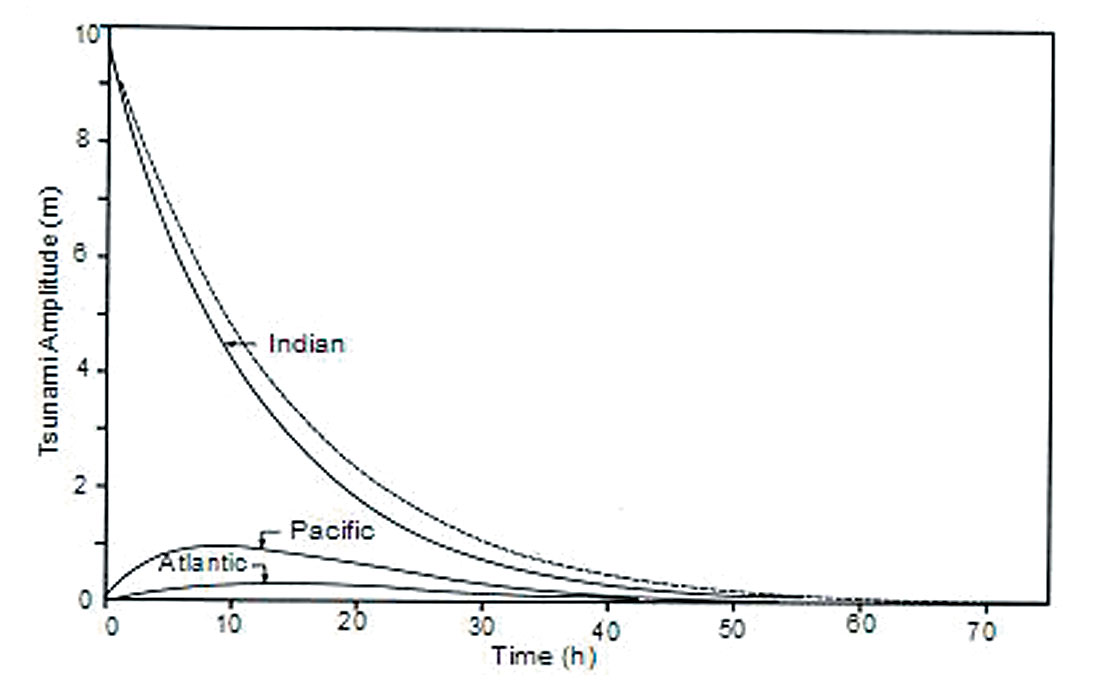
It can be seen from figures that the maximum tsunami amplitude in the Atlantics Ocean is about 1/3 m and in the Pacific Ocean about 0.8 m. These values are comparable to the observed values of 0.3 m and 0.65 m respectively. It can also be seen from figures that the tsunami traveled into the Pacific Ocean earlier than into the Atlantic Ocean, which is borne out by observations.

4. Summary and Conclusions

The Indian Ocean tsunami of 26th December 2004 not only propagated throughout the Indian Ocean, but also propagated into the Pacific and Atlantic oceans. A simple analytical model was adapted to determine approximately this leakage of tsunami energy from the Indian Ocean into the Pacific and Atlantic oceans respectively, through the gaps between Australia and Antarctica, and between Africa and Antarctica. The computed results show that indeed the tsunami traveled earlier into the Pacific Ocean than into the Atlantic, which agrees with the observations. The model results predicted maximum tsunami amplitude of about 0.8 m in the pacific and about 1/3 of a meter in the Atlantic. These results compare reasonably well with the observed values of 0.65 m in the Pacific and 0.3 m in the Atlantic Ocean.