Keep an eye on your basement! – the 3D version

Summary

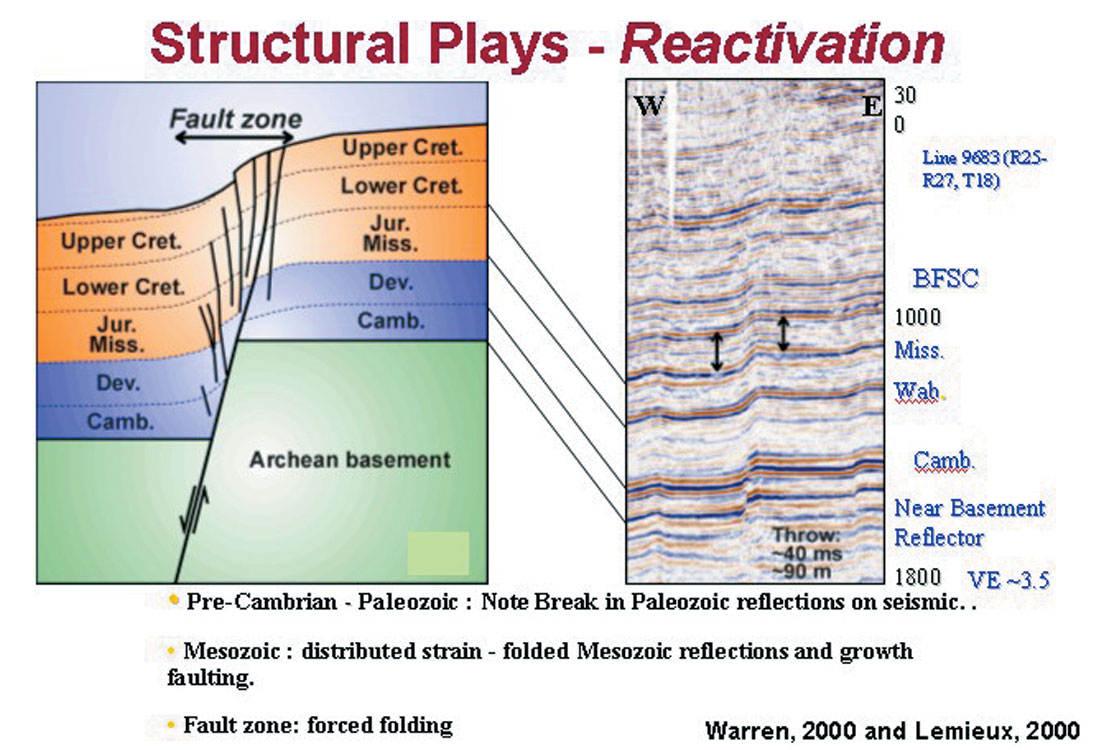
Twenty some years ago Bernard Coulott of Imperial Oil exhorted us to “Keep an eye on your basement!” during a CSEG luncheon talk. In 2004, we presented several wide ranging geological examples of the influence of basement structure on the overlying stratigraphy (Peirce and Griffith, 2004) and emphasized how far up in the section such effects could influence trap and reservoir development (Figure 1). This paper focuses on how to map magnetic basement quickly and effectively in 3D on a seismic work station using High Resolution AeroMagnetic (HRAM) data and new techniques that we have recently developed.

Introduction

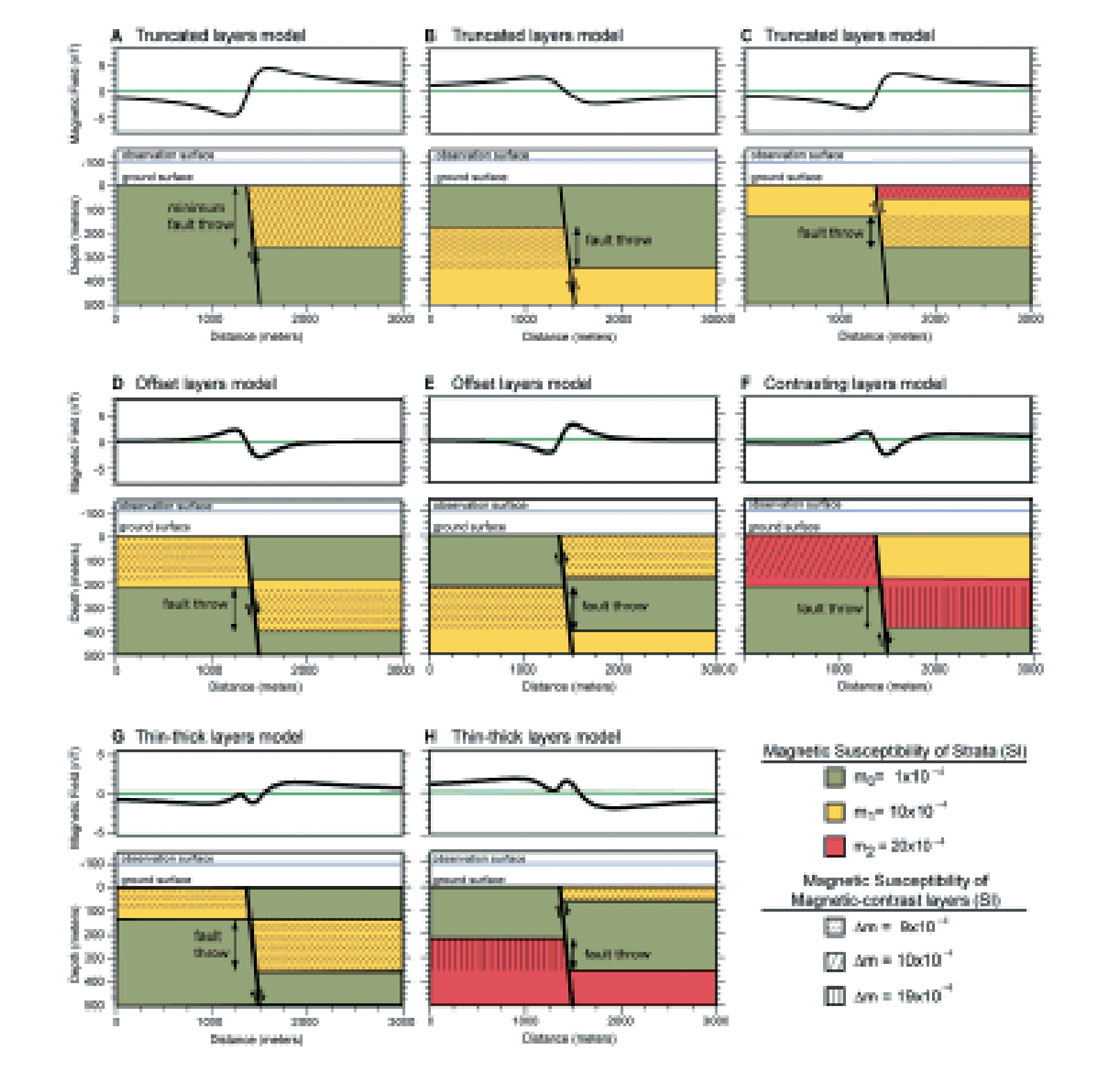
Using airborne magnetic data to map faults in the intra-sedimentary section was not possible until the advent of the Global Positioning Satellite positioning system, which came into use in airborne magnetics in Western Canada in the early 1990’s. With precise positioning, we now fly low altitude drape surveys at 100-150 m above ground, with close line spacing (50 – 800 m), in what is now commonly referred to as High Resolution Airborne Magnetic (HRAM) surveys. The precise positioning removes all spatial aliasing and allows us to map dipping beds that have some susceptibility contrast. More importantly, we can map faults where beds with some susceptibility contrast are offset vertically and produce small (less than 1 nT to a few nT) magnetic anomalies. The model that we use for interpreting such faults comes from the Rio Grande Rift near Albuquerque, New Mexico, where faults offsetting volcaniclastic sediments have very clear magnetic signatures (Grauch, et al., 2001, 2008). Figure 2 shows several examples with widely varying signatures depending on the specific fault geometry.

For many years we have worked on improving our ability to interpret faults and fractures in the basement and in the sedimentary section using HRAM data. The development of the MaFIC cube (Rhodes and Peirce, 1999) was a major step forward as it allowed depth solutions to be imported into a seismic work station in SEG-Y format and compared directly to the seismic data and interpretation using software that the interpreters already had on their desktops. However, our best magnetic depth determinations were usually based on 2D Werner inversion using many operators of different lengths to resolve different depths. The results contained considerable vertical dispersion and it was difficult to be completely confident about our fault interpretations.

We call our completely new interactive process Enhanced 3D Magnetic Depth Inversion (E3D inversion) because the mathematics of Euler and Werner deconvolution (both of which are inversion processes more than deconvolution processes) can be merged into a unified expression using Hilbert transforms. This work builds upon the large volume of work by Richard Hansen of EDCON-PRJ in Denver, and particularly his development of what he called a 3D Werner algorithm (Hansen, 2005; Hansen and Simmonds, 1993; Hansen and Suciu, 2002; Nabighian and Hansen, 2001).

Unfortunately, Richard passed away on Jan. 6, 2008, and this paper is dedicated to him and the rich legacy of ideas and careful thinking that he generously shared with his colleagues.

Method

We have implemented the 3D algorithm with multiple sources, added an interactive GUI interface to make it more user friendly, and applied some statistical coherence functions to effectively sort out tightly grouped solutions from mathematical noise. For 2D Werner calculations, we have optimized the matrix inversion to focus on the best defined matrix values first and thereby greatly reduce the mathematical scatter that has plagued us in the best.

Examples

We have applied this technique to the Bishop model (Flanagan, 2005) which has been used widely in recent years to evaluate magnetic depth inversion techniques. Figure 3 shows a somewhat smoothed model of basement in the Bishop model. The model is based on real topography, buried to the depths shown in Figure 3 beneath non-magnetic sediments, with a simple susceptibility map assigned. There are no faults in the model, only vertical contacts between seven simple magnetic bodies. The forward magnetic field of this model is easily calculated, and the challenge has been to invert the data for the known magnetic basement (Reid et al., 2005; Hassan et al., 2007).

Figure 4 shows the interpreted basement using our E3D approach, calculated from every 10th row and column of the magnetic data of the model. The quality and fidelity of these results as compared to the model depths far exceed anything that we have been able to achieve in the past, both in terms of accuracy and in terms of a wide distribution of solutions that are not restricted just to major fault blocks or lithological contacts.

We will also present results from the Peace River Arch in northern Alberta, integrated with existing well data, and demonstrate how much more detail we can now resolve in the basement structure than we could previously. In this case, the difference is particularly dramatic in the SW portion of the area, well south of the Fort St. John graben system, where there is little well control to basement to constrain our earlier interpretation. Furthermore, because the sediments in northern Alberta have significant susceptibilities, we can map faults within the sedimentary section (see Rhodes and Peirce, 1999, for an example of the Hines Creek Fault).

Conclusions

Understanding how basement structural control influences the overlying section is a critical and undervalued part of the exploration process. Our new approach of E3D inversion offers the chance to develop more complete images of basement than have been possible previously, as well as to image faults within the basement and the sedimentary section more clearly than before. The final result is an attribute cube of magnetic depth solutions that can be compared directly to seismic data on any seismic work station.

Acknowledgements

This paper is the latest effort at trying to understand the influence of basement on faulting and to map those faults using HRAM data. Many have contributed to this effort over the last ten years. In particular, the algorithm for the 3D Werner approach comes from Richard Hansen. The implementation discussed herein was completed by Dave Caulfield and Randy Kolesar.