Limaçon is a French word meaning snail (from the Latin word limax). In the real world, limaçons have a wide range of applications from culinary (a delicacy in some countries) to cosmetics (their slime is used for human skincare). In the mathematical world, limaçons (also known as Pascal’s limaçons after Etienne Pascal, father of Blaise Pascal) have many applications too, from the shape of electrical conductor’s cavity to the study of black holes. In this article I investigate another field of application in geophysics: seismic amplitude variation with offset and azimuth (AVOAz).
Commonly fitted by an ellipse, AVOAz is actually better approximated using limaçons. The article begins by reviewing the properties of the original limaçon, then explains how they can apply to AVOAz and finally illustrates how limaçons can help with the interpretation of anisotropy on real data.
Original limaçon
The original limaçon has a simple mathematical form that hides a lot of complexity. Its expression in polar coordinates is given by:
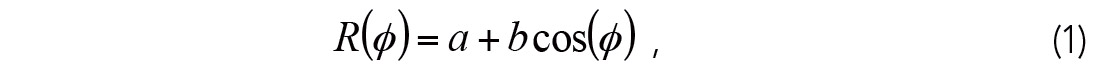
where ϕ is a variable that could represent time (in the study of trajectories for example) or, in the context of this article, the source-receiver azimuth. The parameters a and b control the shape of the limaçon. Figure 1 shows the family of limaçons for different ratios |a/b|.
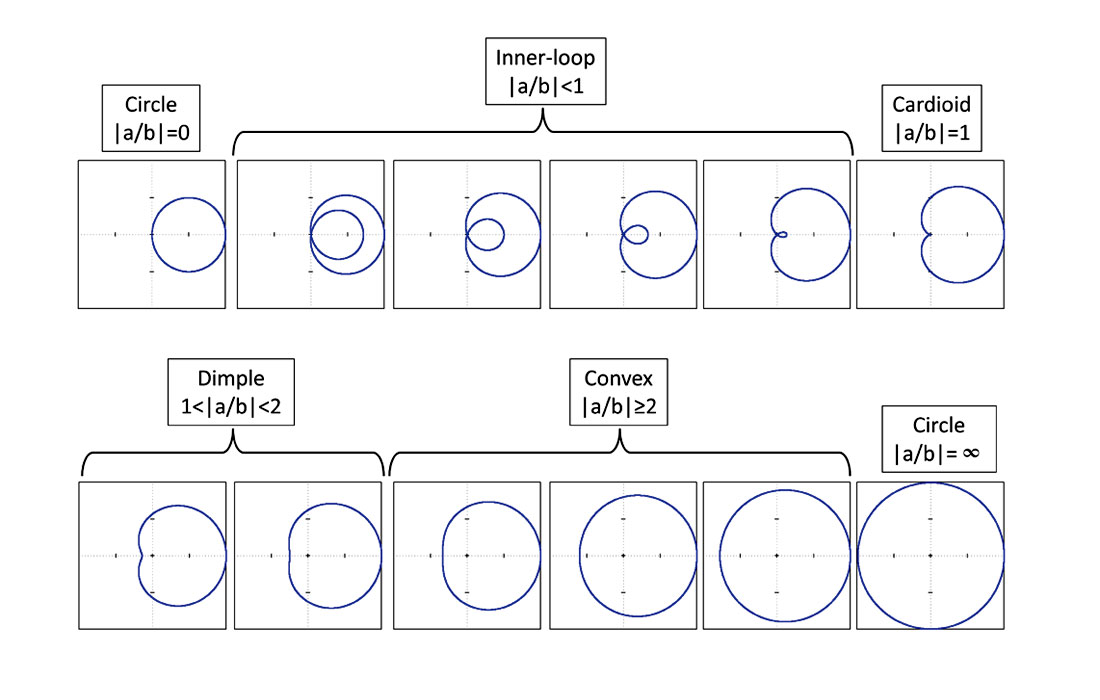
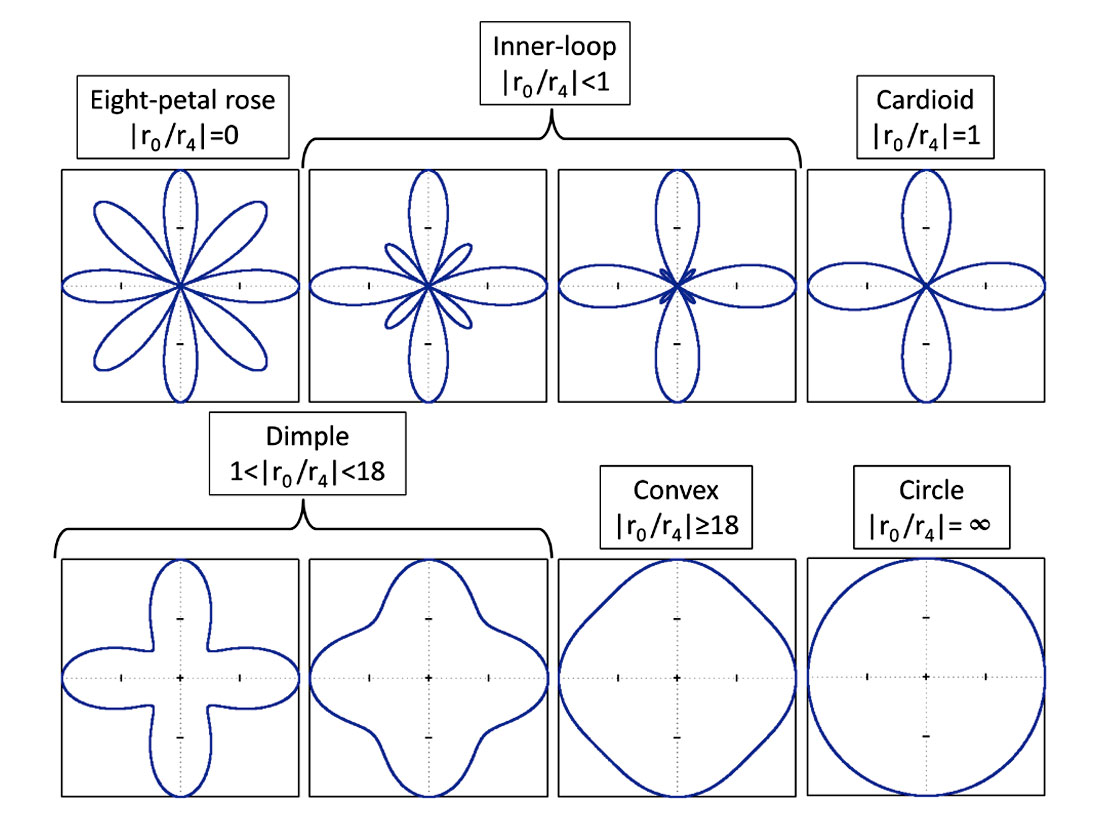
The limit behavior where the ratio is either 0 or infinity describes a circle. In between, as the ratio increases, the limaçon evolves from an inner-loop (|a/b|<1) to a cardioid (|a/b|=1), named after its heartshaped appearance. As the ratio increases further, the limaçon exhibits a dimple (1<|a/b|<2) and finally becomes convex (|a/b|>=2). More classes of limaçons have been defined based on inflexion points such as uniflexional, biflexional and undulational (Gibson, 2001) but are not covered in this article. It is interesting to note that an ellipse can be obtained by taking the inverse of a dimpled limaçon for example.
AVOAz limaçon of 2nd order
AVOAz is used to study azimuthal anisotropy from seismic data, whether the anisotropy is stress-induced and/or fracture-induced. The AVOAz reflectivity, R, can be expressed in terms of Fourier coefficients (e.g. Downton et al., 2011) and for a given angle of incidence, may be written as:
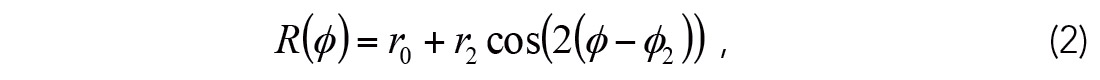
where ri and ϕi (i=0,2) are the magnitude and phase of the ith Fourier coefficient which vary with angle of incidence. Fourier coefficients of order 4 have been discarded in equation (2). This is a common simplification which means assuming the anisotropy is elliptical or approximated using near offsets only, e.g. near offset Rüger equation (Rüger, 1996).
Downton and Roure (2015) discuss the interpretation of the Fourier coefficients for different types of anisotropy. A simple explanation for the scope of this article is that r0 controls the amplitude variation with offset (AVO) of the data and the 2nd and 4th Fourier coefficients control the amplitude variation with azimuth (AVAz): r2 is related to the anisotropic gradient and r4 is a function of the anellipticity.

By comparing equations (1) and (2), it appears that the AVOAz expression has the same form as a limaçon with a different phase (constant phase shift ϕ2 and double phase). Similarly to the original limaçon, the ratio |r0 /r2| controls the shape of the AVOAz curve as illustrated in Figure 2 with ϕ2=0. The same classes are defined but with a few differences:
- Whereas the transformation of the original limaçon occurs on one side only, the transformation of the limaçon described by equation (2) occurs on two sides at the same time (due to the double angle in the phase).
- The class |r0 /r2|=0 no longer describes a circle but a four-petal rose. r0 could be zero for a variety of reasons depending on the angle of incidence, e.g. class II AVO.
- The threshold between the classes “dimple” and “convex” changes due to the double angle of the phase that impacts the computation of the derivatives of equation (2).
I keep the name “cardioid” by analogy to the original limaçon even though a more appropriate term would be a lemniscate due to its figure-eight shape. The class |r0 /r2|= ∞ corresponds to the isotropic or VTI/polar anisotropy case (r2=0) or negligible azimuthal anisotropy (r2<<r0) which is indeed described by an azimuthally invariant circle.
Even though equation (2) corresponds to elliptical anisotropy, it does not lead to elliptical AVOAz shapes in Figure 2 but the ellipticity rather refers to the P-wavefront (Thomsen, 2002, pages 1-31 to 1-33).
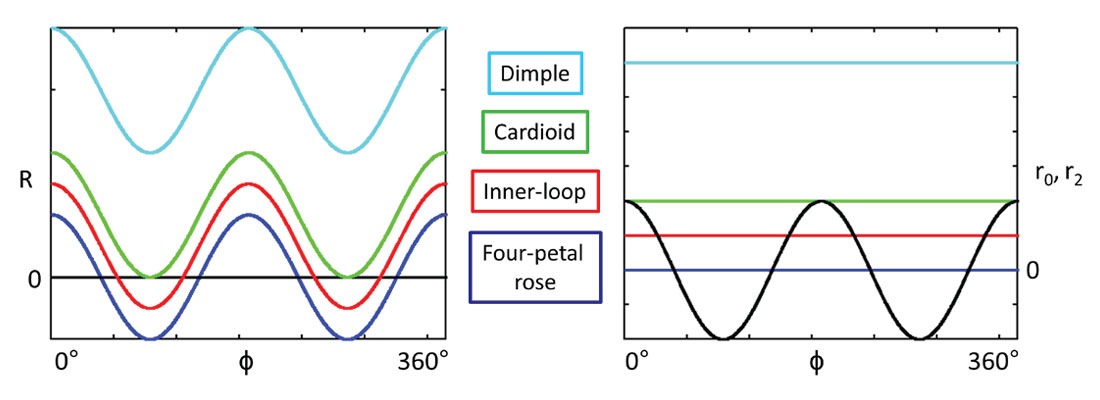
The limaçon can also be displayed in amplitude versus azimuth plots. Figure 3 (left) shows the reflectivity R as a function of azimuth for different classes represented by different colors. It appears that two of the four petals correspond to positive values and the other two to negative values. In the same way, the inner-loops correspond to different amplitude sign. The cardioid occurs when the minimum (or maximum) amplitude is zero. The amplitudes of the other classes (dimple, convex, circle) are strictly positive (or negative). The reflectivity R can be decomposed into individual Fourier coefficients (Figure 3, right): the 2nd order is fixed in black while the constant 0th order (color lines) varies transforming the limaçon from one class to the other.
If the phase ϕ2 changes in equation (2), the limaçon rotates as illustrated in Figure 4. Adding 90° to ϕ2 or changing the sign of r2 results exactly in the same curve. Therefore the orientation of the limaçon cannot be used to interpret the anisotropy orientation without ambiguity.
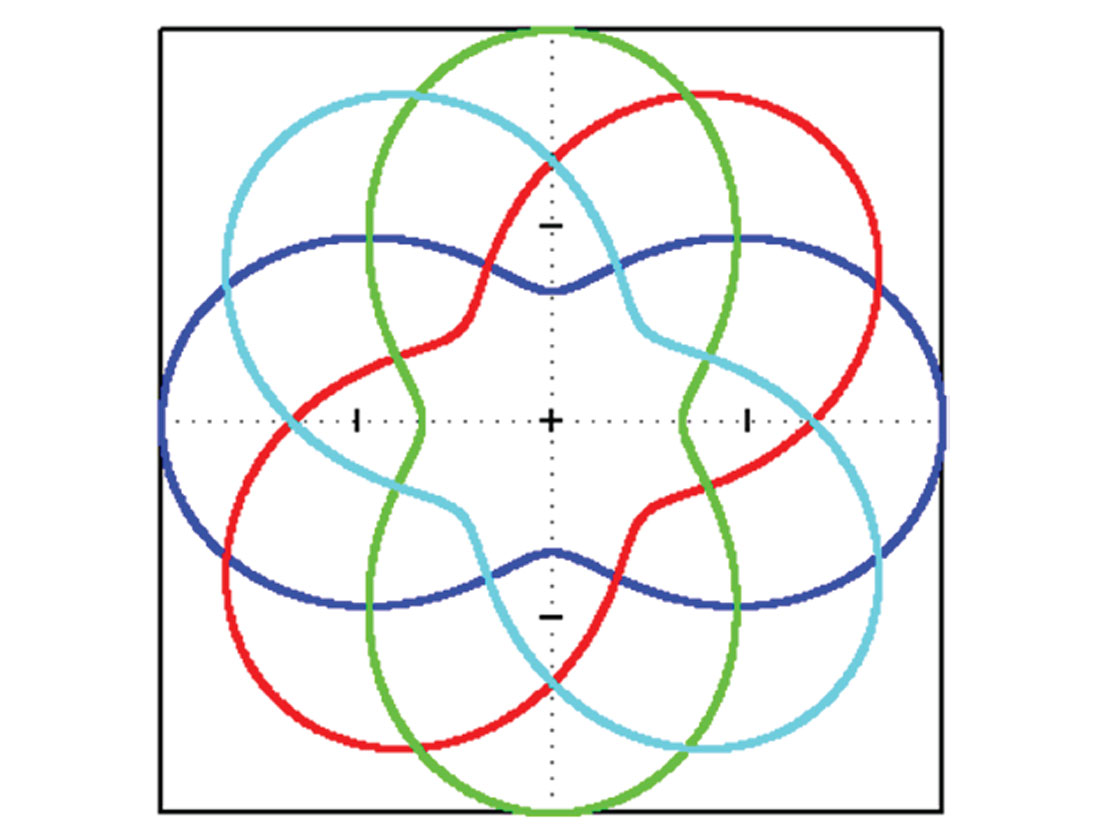
The AVOAz limaçon of 2nd order closely resembles the gradient equation given by Rüger (1996):

where Biso is the azimuthally invariant part of the gradient B, Bani is the anisotropic contribution and ϕsym is the direction of the symmetry-axis plane (perpendicular to fractures for example). The difference is that the double phase in equation (2) becomes a square in equation (3) but similar conclusions can be drawn. The ratio |Biso/Bani| controls the shape of the limaçon (see for example Figure 5.6 in Rüger, 1996 and also Liu and Ogloff, 2005) and the same orientation ambiguity occurs if the sign of Bani flips or if the phase ϕ sym changes by 90°. However the interpretation of the gradient equation (3) is different from the AVOAz equation (2). Biso and Bani are not dependent on the angle of incidence while r0 and r2 are: Biso and Bani are parameter driven while r0 and r2 are data driven.
Another application of the limaçon of 2nd order is the possibility to analyze velocity variation with azimuth (VVAz). However this article focuses only on amplitudes.
AVOAz limaçon of 4th order
Before adding the 4th Fourier coefficient to equation (2), I look at its contribution separated from the 2nd Fourier coefficient and consider the following AVOAz reflectivity expression:
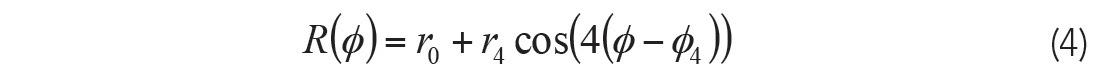
Figure 5 shows the evolution of the associated limaçon as the ratio |r0 /r4| increases and ϕ4=0.
The transformation of the limaçon now occurs in four different directions simultaneously due to the increased phase periodicity in equation (4). The class |r0 /r4|=0 now describes an eight-petal rose and the cardioid class resembles the four-petal rose from the AVOAz limaçon of 2nd order (Figure 2). As in the previous case, the threshold between the classes “dimple” and “convex” changes because of the impact of the phase on the derivatives. Again, the limaçon rotates as the phase ϕ4 changes.
Extended AVOAz limaçon
A more general form of AVOAz is obtained by combining equations (2) and (4) as follows:

This expression no longer corresponds to the original limaçon and is referred to as an extended limaçon which is the sum of two limaçons with different phases. Figure 6 shows the evolution of this extended limaçon for different ratios |r0 /r2| and |r0 /r4| when the phase shifts ϕ2 and ϕ4 are equal to 0.
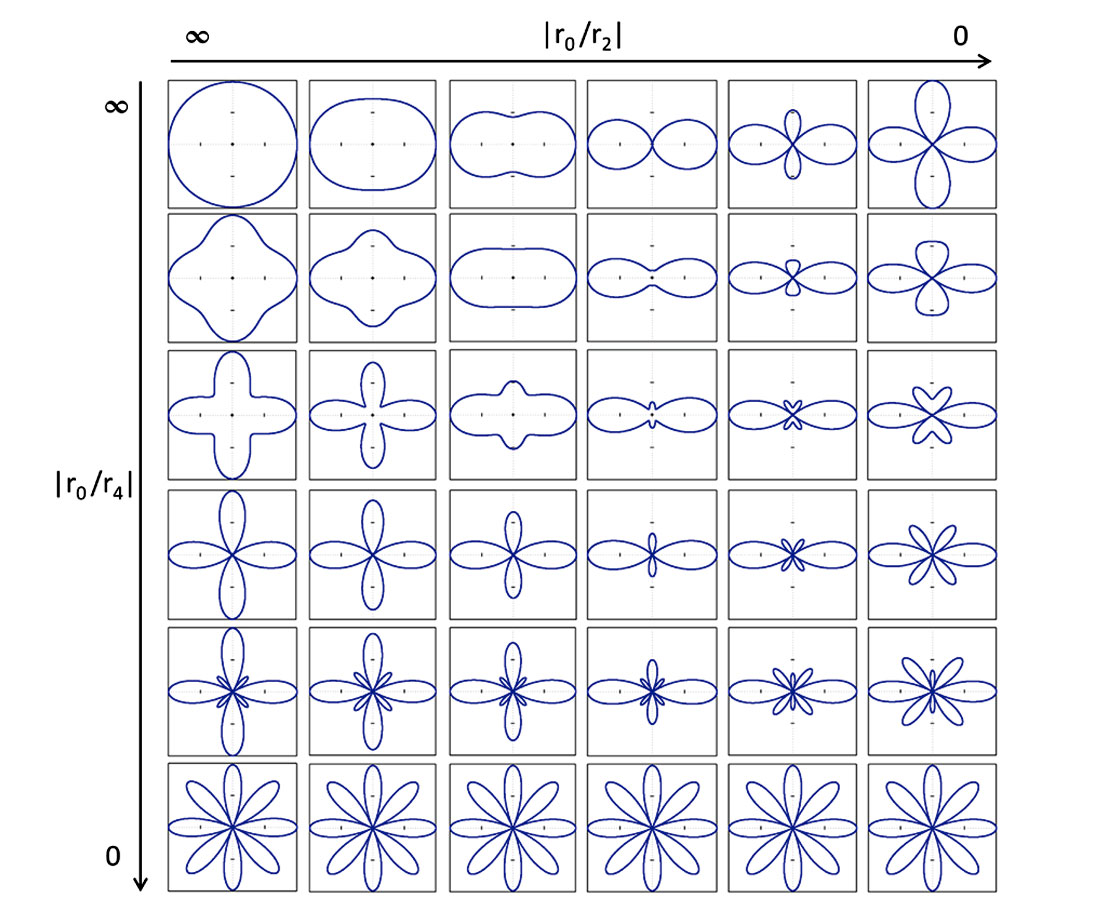
The shapes shown in Figure 6 are not exhaustive and are meant to be read by column from top to bottom, describing the growing impact of the 4th Fourier coefficients on the AVOAz limaçon of 2nd order (depicted in the top row). The scale is non-linear in that the main diagonal does not correspond exactly to |r2 /r4|=1 but above this diagonal the influence of r2 is generally larger than r4. Starting from the two columns on the left, the circle and convex classes of 2nd order follow the transformation of the limaçon of 4th order (Figure 5), evolving progressively through the dimple, cardioid, inner-loop and eight-petal rose classes. In the two columns in the middle, the dimple and the cardioid progressively grow a petal under the increasing influence of the 4th Fourier coefficient, until reaching the cardioid threshold. The shape is further modified by the growth of four innerloops that eventually reach the eight-petal rose class. Finally in the two columns on the right, the inner-loop of 2nd order and four-petal rose are increasingly squeezed vertically by the 4th Fourier coefficient to create a dimple that further splits into two smaller distinct petals when reaching the cardioid class. Then two inner-loops of 4th order appear vertically in the middle and grow into full petals to reach the eight-petal rose class.
The transformations illustrated in Figure 6 get more complicated as the difference between the phase shifts ϕ2 and ϕ4 gets larger. A phase difference (ϕ2 ≠ϕ4) will introduce an asymmetry in the shapes (Figures 7f and 7g), except if the difference is a multiple of 45°, in which case the transformation of the limaçon on the far right column for example would occur horizontally rather than vertically, but still in a symmetrical way.
Some methods, such as the non-linear inversions of Fourier coefficients (Downton et al., 2011) or of statistical moments (Roure, 2014), and methods based on the Rüger equation (1996), rely on the assumption that the phases ϕ2 and ϕ4 are equal. The assumption ϕ2=ϕ4 is valid for different types of anisotropy: in the case of a single set of vertical fractures in an isotropic background, whether the fractures are rotationally invariant (i.e. HTI) or variant (i.e. VFI), or even if the background is transversely isotropic (VTI) resulting in VFTI anisotropy. In all those cases, if the media have the same mirror planes, then the phase of the 2nd and 4th Fourier coefficients is the same. If the phase is different, it suggests that the previous assumptions are violated (Downton and Roure, 2015). In other words, anisotropy other than HTI, VFI or VFTI or media with different mirror planes result in different phases. In the case of two or more non-orthogonal sets of vertical fractures, the assumption ϕ2=ϕ4 is still valid when the normal to tangential compliance ratio is 1 and each fracture set has equal weight (Sayers and Dean, 2001). In the case of HTI media with different mirror planes, methods such as the simultaneous elastic inversion of azimuthal angle stacks (Downton and Roure, 2010) or of azimuthal Fourier coefficients (Roure and Downton, 2012) can handle the asymmetry of the extended AVOAz limaçon.
The 4th Fourier coefficient is an expression of the anellipticity of the anisotropy which does not imply asymmetry of the shape of the AVOAz limaçon (which is caused by the difference in phases). It does however imply that the amplitude distribution is asymmetric, which is a measure of the skewness (Roure, 2014). If stress-induced anisotropy is assumed to be elliptical (Gurevich and Pervukhina, 2010), then the AVOAz would look like the limaçons in Figure 2 where the 4th Fourier coefficient is null. There is however some non-uniqueness in the shapes, e.g. an inner-loop such as the one in Figure 2 (1st row, 3rd column) also appearing in Figure 6 (4th row, 4th column) where the 4th Fourier coefficient is not null. However, if a distinct contribution from the 4th Fourier coefficient is observable, e.g. from the number and size of petals, then the anisotropy is anelliptical (either due to fractures only, or most likely both stress and fractures). This distinction is not possible using an ellipse only.
The interpretation of the shape of the limaçons is mostly based on the ratio of Fourier coefficients. Figures 2, 5 and 6 display a whole range of shapes within the mathematical limits of the parameters. Using rock physics, it is possible to reduce the range of the ratios and limit the shapes of the limaçons to physical ones, hence reducing the non-uniqueness between the shapes and simplifying the interpretation. Linear slip theory (Schoenberg, 1980) can be used to relate the Fourier coefficients ratios to more meaningful properties such as the fracture compliances and weaknesses. For example, in the case of asymmetric fractures, the ratio of the horizontal to vertical compliances controls the relative magnitudes of the 2nd and 4th Fourier coefficients (Downton and Roure, 2015).
Real data example
After reviewing many different theoretical shapes of limaçons, I look at real data examples from West Central Alberta, Canada (see Downton et al., 2011, for more details on the dataset). Figure 7a shows the 8 azimuthal angle stacks available for this study at an angle of incidence of 35°. Corresponding Fourier coefficients are also displayed (Figure 7b). I now try to interpret AVOAz curves selected spatially throughout the dataset using limaçons (Figures 7c to 7g).
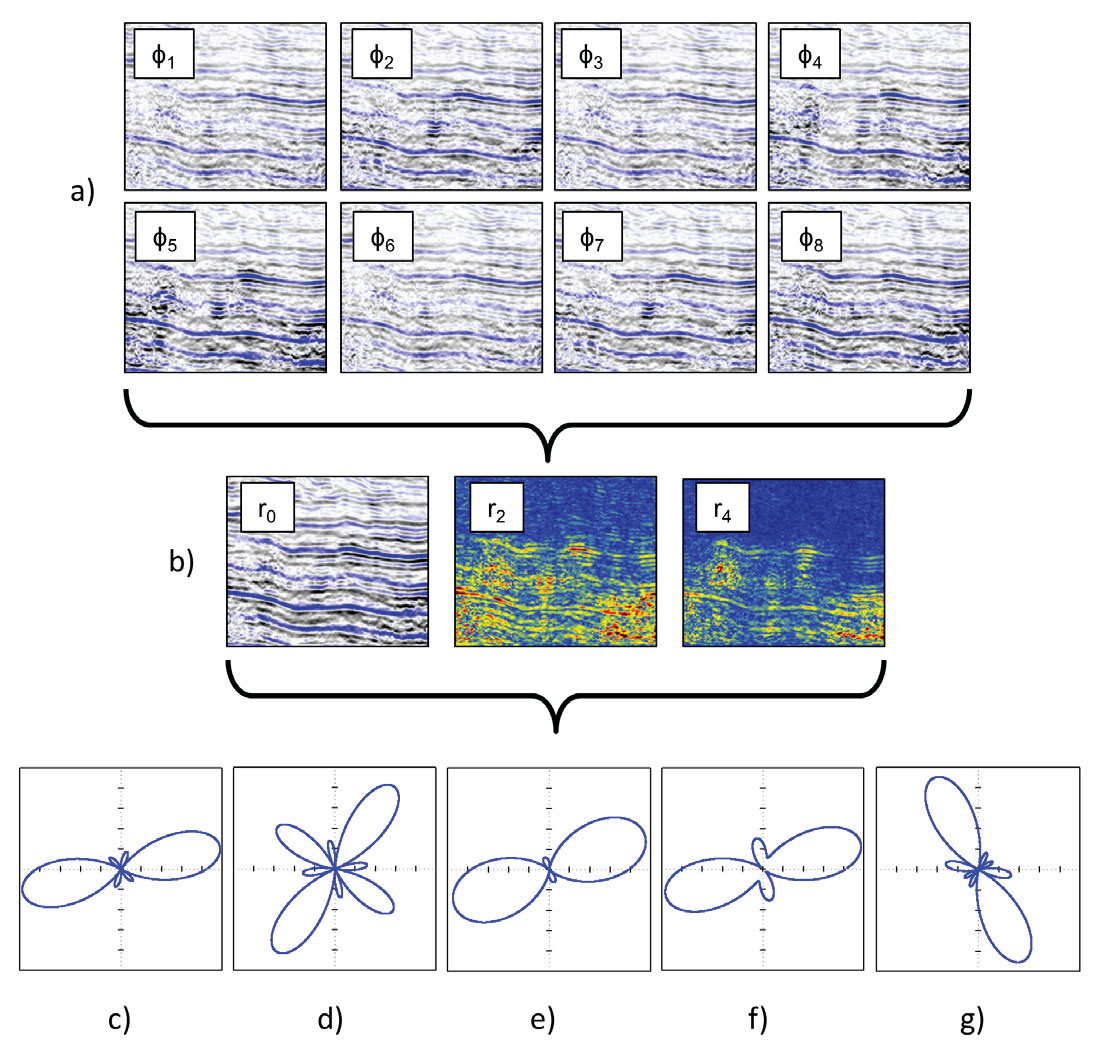
The extended AVOAz limaçon shown in Figure 7c clearly presents characteristics coming from the 4th Fourier coefficients. The four thinner loops or petals could not be coming from a 2nd order limaçon alone and are due to the 4th Fourier coefficient splitting 2nd order inner-loops into thinner loops (Figure 6, 5th column, 4th row). This is a strong indication that the anisotropy is due to the presence of fractures. This limaçon is obviously rotated and the relative size of the thinner petals compared to the larger ones indicates that the 2nd Fourier coefficient is larger than the 4th. The symmetry of the shape also indicates that the phases of the 2nd and 4th order limaçons are very close (±45°).
The strong features of a 4th order limaçon are easily identified on Figure 7d by comparison to Figure 6 (3rd column, 5th row). The impact of the 2nd Fourier coefficient is still visible since the 4 larger petals have different size depending on the direction, but its magnitude seems to be smaller than the one of the 4th Fourier coefficient. This limaçon is also rotated and symmetrical, suggesting the phases do not vary significantly.
The non-uniqueness between the shapes mentioned previously is illustrated on Figure 7e. It could either be an inner-loop of 2nd order (Figure 2) or the transformation of a cardioid of 2nd order under the influence of the 4th Fourier coefficient just before the 4th order inner-loops appear (Figure 6, 4th column). Here again the limaçon is rotated and symmetrical.
The difference in phase between ϕ2 and ϕ4 is illustrated on Figure 7f and appears with the asymmetry of the shape. Since the impact of both phases is visible, the anisotropy is coming from both 2nd and 4th Fourier coefficients. The shape is similar to the transformation of the cardioid of 2nd order under the influence of the 4th Fourier coefficient (Figure 6, 4th column, 3rd row) and suggests significant contribution from both Fourier coefficients.
The last example also shows an asymmetric shape (Figure 7g) due to the difference between the phases of the 2nd and 4th order limaçons. The 4th Fourier coefficient has modified a 2nd order inner-loop but in an asymmetric way compared to Figure 6 (5th column, 5th row). Such a transformation requires large Fourier coefficients of both orders 2 and 4. The limaçon orientation seems to be perpendicular to the previous limaçons because the ratio |r0 /r2| and |r0 /r4| are both negative in that case.
Discussion
The interpretation of the extended AVOAz limaçon is complicated by the fact that AVO and AVAz are mixed in its formulation, i.e. its shape depends not only on the |r2 /r4| ratio (AVAz) but also on the relative magnitude of r2 and r4 compared to r0 (AVO). The benefit of separating AVOAz into AVO and AVAz for interpretation (Downton and Roure, 2015) applies also to the visual interpretation using limaçons. By removing the r0 AVO term from equations (2), (4) and (5), the limaçon now enters the “rose” family. Equation (5) becomes the sum of two roses with different number of petals: four for the 2nd order (equation 2 and Figure 2, 1st row, 1st column) and eight for the 4th order (equation 4 and Figure 5, 1st row, 1st column). The shape of the AVAz rose then only depends on the |r2 /r4| ratio and difference between the phases ϕ2 and ϕ4 .
The |r2 /r4| ratio can also be used as a processing QC attribute. It’s a particular case of the Anellipticity Coefficient defined by Araman and Paternoster (2014) to measure the contribution of Fourier coefficients of different orders and may be used to identify areas of high azimuthal noise.
Finally, the AVOAz classes mentioned in this article are simply based on the shape of the limaçon and analytic geometry (rose, inner-loop, cardioid, dimple, convex, circle). Other classifications exist like the anisotropic AVO classes based on the sign of the anisotropic gradient (Perez, 2010).
Conclusions
Though an ellipse approximation for AVOAz may be valid in some cases (mostly for near offset assumptions), the general shape of AVOAz is more complex and ellipse fitting methods may introduce significant bias. This article presents a more accurate approximation using limaçons whose shape is controlled by Fourier coefficients ratios and phases. The more complex behavior of the limaçon allows extracting more information about anisotropy compared to the standard ellipse parameters. The interpretation is complicated by the non-uniqueness of the shapes, the phase difference between the coefficients and a 90° ambiguity in the orientation. However, the limaçon provides a simple visual qualitative interpretation tool that helps understand the influence of each Fourier coefficients on the overall AVOAz. The interpretation can be further quantified by using rock physics to reduce some of the ambiguities and provide the interpreter with more meaningful anisotropy properties.

Acknowledgements
I would like to thank Jon Downton, Brian Russell and Dan Hampson at CGG for their valuable comments.










Join the Conversation
Interested in starting, or contributing to a conversation about an article or issue of the RECORDER? Join our CSEG LinkedIn Group.
Share This Article