How AVO Can be a Multiple Attenuator

Unintended benefits

Sometimes there are spin-off benefits to developing a technology. From NASA’s space technology program, for instance, we have benefited from unintended applications such as fireproof suits for auto racers, laser angioplasty, advanced digital imaging for biopsies, and programmable pacemakers. While programmable pacemakers clearly were not directly developed for space travel, sometimes when you develop technology, valuable applications follow.

Quantitative AVO analysis can produce some spin-off applications too, such as multiple attenuation. How can AVO be a multiple attenuator? In essence, the answer is in the assumptions of Zoeppritz’s equations, and how they differ from the real-world seismic wavefronts that travel in the subsurface. Zoeppritz’s equations describe plane waves and apply to a reflection between two half-spaces, and so do not include wavelet interference effects caused by layering. AVO analysis uses Zoeppritz’s equations (or some linear approximation of the equations) to describe pre-stack amplitude behavior. An unintended benefit is that, due to the assumptions of Zoeppritz, a Zoeppritz-based AVO inversion will consider multiples and converted waves to be noise. That is, the AVO analysis will see multiples as noise, and will exclude them in its reconstruction.

Backing up a bit: how AVO analysis works

Zoeppritz’s equations relate reflection coefficients as a function of angle of incidence to the underlying rock properties that caused the amplitude variations. When a seismic wavefront travels at some angle through a rock and reflects from a second rock layer, the strength of the reflection will vary with angle. This variation in amplitude is determined by just two things: the angle and the contrast in physical properties - how different the reflecting rock layer is from the overlying rock. (The inverse problem then is to unlock physical properties of the second rock by examining the amplitude behavior of the seismic reflection. In simplest terms, this is the basis of estimating rock properties from AVO analysis.)

But Zoeppritz’s equations are unwieldy, and so to carry out AVO analysis, often a simpler approximation of Zoeppritz’s equations is fit to the observed pre-stack amplitudes. For example, we may fit Shuey’s familiar approximation:

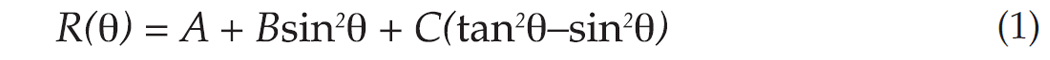
where

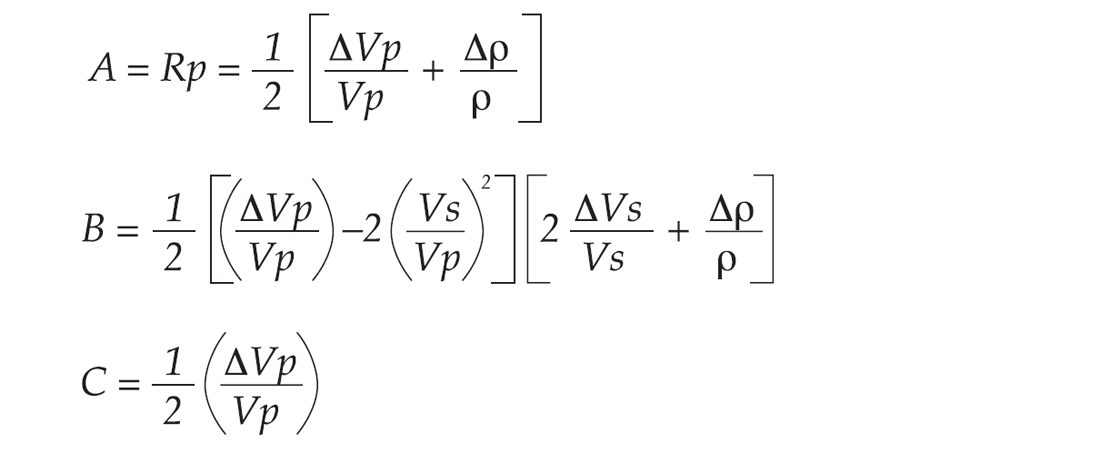
or Fatti’s approximation:

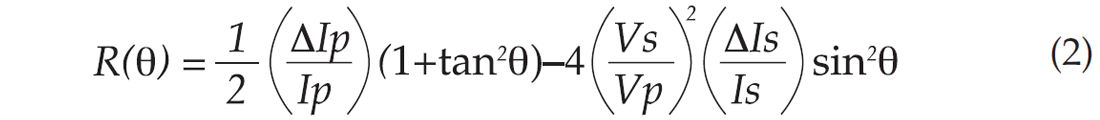
to the observed pre-stack amplitudes. (Yes, these really are simplified approximations.) Let’s say we fit Fatti’s equation to the observed pre-stack amplitudes (R(θ) in Equation 2) to estimate P and S reflectivity (ΔIp/Ip and ΔIs/Is in Equation 2). Then with this equation solved, we can reconstruct the gather: we know all the terms on the right hand side of the equation, and we have a mapping between angle and offset.

AVO as a multiple attenuator

We can illustrate with a typical multiple-laden gather from western Canada. Figure 1a is a cdp supergather with some offset mixing (that is, an Ostrander gather). A 31 degree angle mute is applied, as the AVO analysis will be restricted to 31 degrees. Multiples in the original gather will, quite properly, not be modeled by the AVO equation and will not be reconstructed.

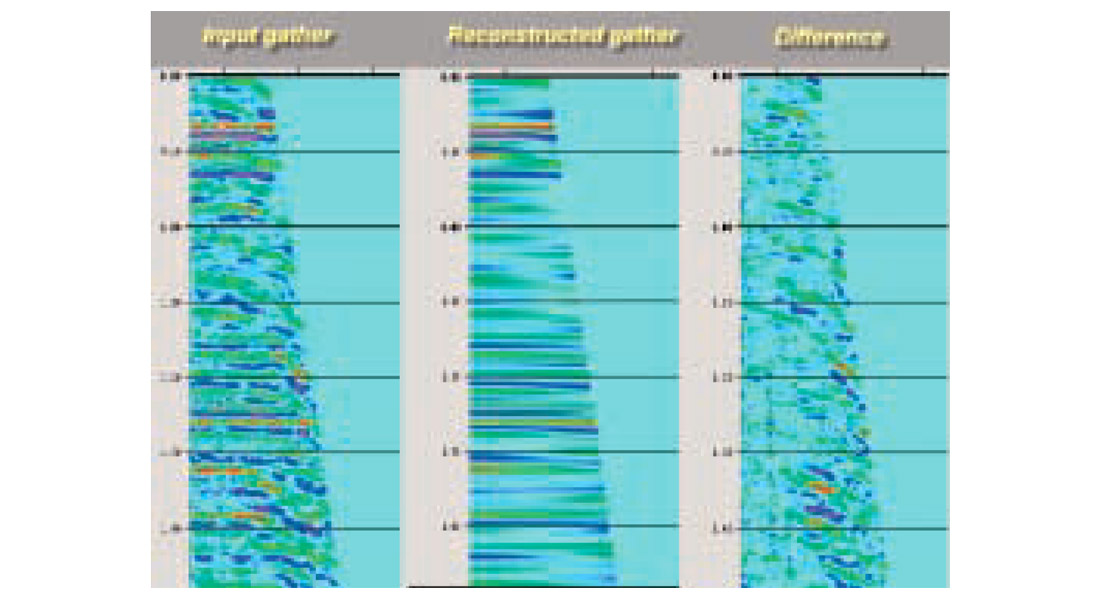
Figure 1b shows the reconstructed gather: the P- and S-reflectivities are extracted via fitting to Fatti’s equation; then with the equation solved, we work backwards and reconstruct (“model”) the gather. Figure1c is the difference between the input gather and the reconstructed (“modeled”) gather. The input - minus - reconstruction gather shows us what is considered noise by the AVO equation. The original intention for this type of display was as a QC to check how well any AVO estimation is working. For example, if we see primary energy on the difference gather, this is a red flag that the AVO solution may be unreliable. Generally, the AVO extraction does work well, and what one sees on a difference gather are random noise and multiples: things that didn’t fit to the AVO equation. In Figure 3c we see the multiples on the difference display, which means multiples are being ‘discarded’ by the AVO reconstruction.

What does this mean? An AVO extraction to estimate zero-offset P-reflectivity can be considered a multiple attenuator! An excellent reason to interpret the NIP section instead of a cmp stack.