Developments in seismic anisotropy: Treating realistic subsurface models in imaging and fracture detection

Introduction

The scope of recent advances in the field of seismic anisotropy is too wide to be thoroughly analyzed in a short overview article. Here, our goal is to emphasize several key recent developments and trends and give a limited number of essential references.

After several decades of mostly theoretical studies, in the late 1990’s anisotropy rapidly moved into the mainstream of seismic exploration and monitoring (for a detailed historical overview, see Helbig and Thomsen, 2005). The increased attention to anisotropy in the exploration community is underscored by the popularity of Leon Thomsen’s classical article on transversely isotropic (TI) media (Thomsen, 1986), which has become the top-cited paper ever published in the journal Geophysics. In part, anisotropy was brought to the forefront of reflection seismology by the acquisition and processing of high-quality multicomponent offshore surveys. Ubiquitous depth mis-ties between PP and PS-wave sections could not be reconciled without introducing transverse isotropy or even azimuthal anisotropy into the velocity fields. Another significant factor was a breakthrough in velocity analysis for the most commonly used anisotropic model – transverse isotropy with a vertical symmetry axis (VTI). It was shown that all P-wave time-processing steps in VTI media are controlled by just the zero- dip normal-moveout (NMO) velocity and the “anellipticity” parameter η that can be estimated from surface reflection data (Alkhalifah and Tsvankin, 1995). This result and several followup developments have made VTI processing of P-wave data a practical endeavor and lent credibility to velocity-analysis algorithms for more complicated anisotropic models.

Whereas looking “past” anisotropy (i.e., correcting for anisotropy in imaging) was the primary focus of anisotropy research in the 1990’s, it is becoming increasingly important to use the estimated anisotropic parameters in reservoir characterization and lithology discrimination. We believe that this trend toward operating with physically plausible anisotropic models and treating their parameters as seismic attributes will continue well into the future.

Imaging of Narrow-Azimuth P-wave Data

For narrow-azimuth P-wave data acquired in the bulk of conventional 3D surveys, the subsurface usually can be approximated by TI models with a vertical or, sometimes, tilted symmetry axis. Most of the early successes of anisotropic P-wave processing were in time-domain velocity analysis and imaging for VTI media because the only relevant anisotropy parameter (η) could be determined from either nonhyperbolic or dip moveout (e.g., Toldi et al., 1999). Although anisotropic parameter-estimation algorithms can operate directly with prestack reflection traveltimes, the work by Van der Baan and Kendall (2002, 2003) shows that there are certain advantages in performing both modeling and inversion for layer-cake VTI media in the τ -p domain. For a comprehensive overview of anisotropic time processing of P-wave data, we refer the reader to Tsvankin (2005).

The advent of depth imaging in general and prestack depth migration in particular has made it imperative to go beyond η-estimation and resolve the vertical velocity V_P0 and Thomsen parameters ε and δ separately. Unfortunately, V_P0, ε, and δ can seldom be constrained by P-wave reflection moveout alone. Therefore, much attention in recent years has been devoted to integrated model building that involves combining P-wave reflection data with borehole information (e.g., check shots or well logs) using geological constraints (Bear et al., 2005). Application of anisotropic depth-migration algorithms to the resulting models produces sections with an accurate depth scale and proper positioning of steeply dipping features, such as flanks of salt domes.

A promising approach to VTI velocity analysis in the depth domain is based on using so-called factorized media with linear velocity variation, in which the anisotropic parameters are constant, while the velocity V_P0 is a linear function of the spatial coordinates (Williamson et al., 1999). Factorized VTI is the simplest model that (1) allows for anisotropy and can describe vertical and lateral velocity variations; (2) permits full understanding of the inherent ambiguities; and (3) requires minimal a priori information to estimate the relevant parameters (Sarkar and Tsvankin, 2004a). By applying migration velocity analysis (MVA) to a section composed of factorized VTI blocks or layers, one can construct realistic heterogeneous anisotropic velocity models for depth migration. In the absence of significant velocity jumps across layer boundaries, knowledge of the vertical velocity at the top of a piecewise-factorized VTI medium is sufficient to estimate V_P0, ε, and δ throughout the section using only P-wave data (Sarkar and Tsvankin, 2004b). Imaging improvements that can be achieved by anisotropic MVA and prestack depth migration are illustrated in Figure 1.

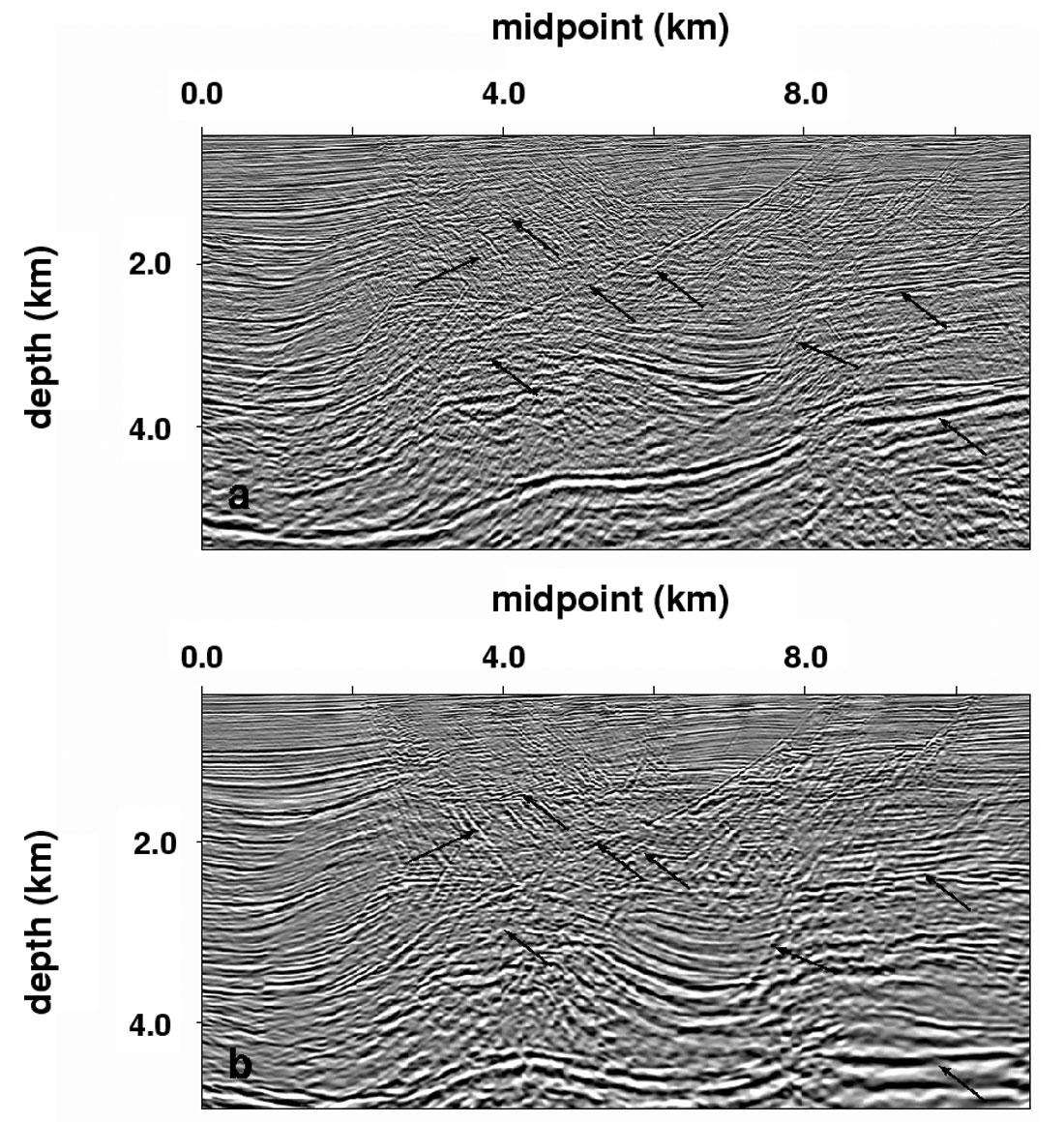
Extension of these new MVA algorithms to 3D data and TI media with a tilted symmetry axis should result in more accurate and realistic anisotropic velocity models as well as improved structural interpretation in such complex areas as the Canadian Foothills.

Multi-azimuth P-Wave Moveout and AVO Analysis

Seismic signatures measured in wide-azimuth reflection surveys may be strongly influenced by azimuthal anisotropy associated with natural fracture systems, nonhydrostatic stresses, or dipping TI layers (e.g., shales). Hence, the azimuthal variation of traveltimes, amplitudes and, possibly, attenuation coefficients can provide valuable information about the medium parameters. Azimuthal moveout and AVO (amplitude variation with offset) analysis of P-wave data have already shown their effectiveness in seismic characterization of fractured reservoirs.

Processing and traveltime inversion of wide-azimuth, conventional- spread data is based on the concept of the NMO ellipse and on Dix-type averaging equations for azimuthally anisotropic media (Grechka and Tsvankin, 1999). Recent experimental studies confirmed that the orientation of the P-wave NMO ellipse can often serve as an indicator of the dominant fracture direction. For example, Jenner (2001) developed a trace-correlation approach to estimate NMO ellipses and applied his methodology to wide-azimuth data acquired above a fractured reservoir at Weyburn field in Canada. His results show that over most of the study area the semi-major axis of the NMO ellipse is aligned with the polarization vector of the fast S-wave, which implies that the medium symmetry is HTI (TI with a horizontal symmetry axis) or orthorhombic. Still, there are indications of symmetries lower than orthorhombic at some locations where the NMO ellipse is rotated with respect to the shear-wave polarization directions.

Quantitative inversion of the P-wave NMO ellipse for fracture parameters, however, suffers from ambiguity that can be reduced by using long-offset traveltimes, prestack amplitudes, shear-wave data (e.g., the vertical times and NMO ellipses of the split S-waves), or borehole information. In particular, long-spread P-wave data acquired over effective orthorhombic models can be inverted for the anellipticity parameters η⁽¹⁾ and η⁽²⁾ that control the azimuthal variation of nonhyperbolic moveout (Vasconcelos and Tsvankin, 2004).

Application of moveout inversion methods in reservoir characterization is often hampered by their limited vertical resolution. Indeed, many fractured reservoirs are relatively thin compared not just to their depth but also to seismic wavelength. Therefore, evaluation of fracture compliances often requires higher-resolution seismic methods that operate with the amplitudes and, potentially, waveforms of reflected arrivals. The main advantages of anisotropic AVO inversion (an excellent overview can be found in Rüger, 2001) include the possibility to resolve the reflection coefficient at the target horizon and the high sensitivity of body-wave reflectivity to the anisotropic parameters.

Most existing P-wave AVO algorithms (e.g., Hall and Kendall, 2003) assume the HTI medium resulting from a single set of aligned penny-shaped cracks, even though this model is regarded as too simplistic for many fractured reservoirs (Bakulin et al., 2000). Still, Gray et al. (2002) and Gray and Todorovic-Marinic (2004) report a number of successful case studies of HTI-based azimuthal AVO analysis, where the estimated fracture direction was in good agreement with the results of other methods. It should be noted that, even for HTI media, inversion of the azimuthally varying P-wave AVO gradient for the crack density is non-unique without additional information (e.g., one obtains different crack densities for dry and fluid-filled cracks). The stability of AVO analysis can be improved by combining wide-azimuth PP, PS, and (if available) SS data (Bakulin et al., 2000; Jílek, 2002; DeVault et al., 2002).

The transformation of seismic amplitudes measured at the surface into the reflection coefficients at the target horizon involves corrections for the source signature and propagation phenomena along the raypath. Major amplitude distortions in anisotropic media, in particular for wide-azimuth data, are caused by the directionally varying geometrical spreading above the reflector (Maultzsch et al., 2003; Tsvankin, 2005). The most practical way to correct for anisotropic geometrical spreading is by expressing it through the spatial derivatives of reflection traveltimes. The move-out-based geometrical-spreading correction was originally developed for VTI media (Ursin and Hokstad, 2003) and later extended to wide-azimuth, long-spread data acquired over azimuthally anisotropic formations (Xu et al., 2005).

Multicomponent Seismic and Mode Conversions

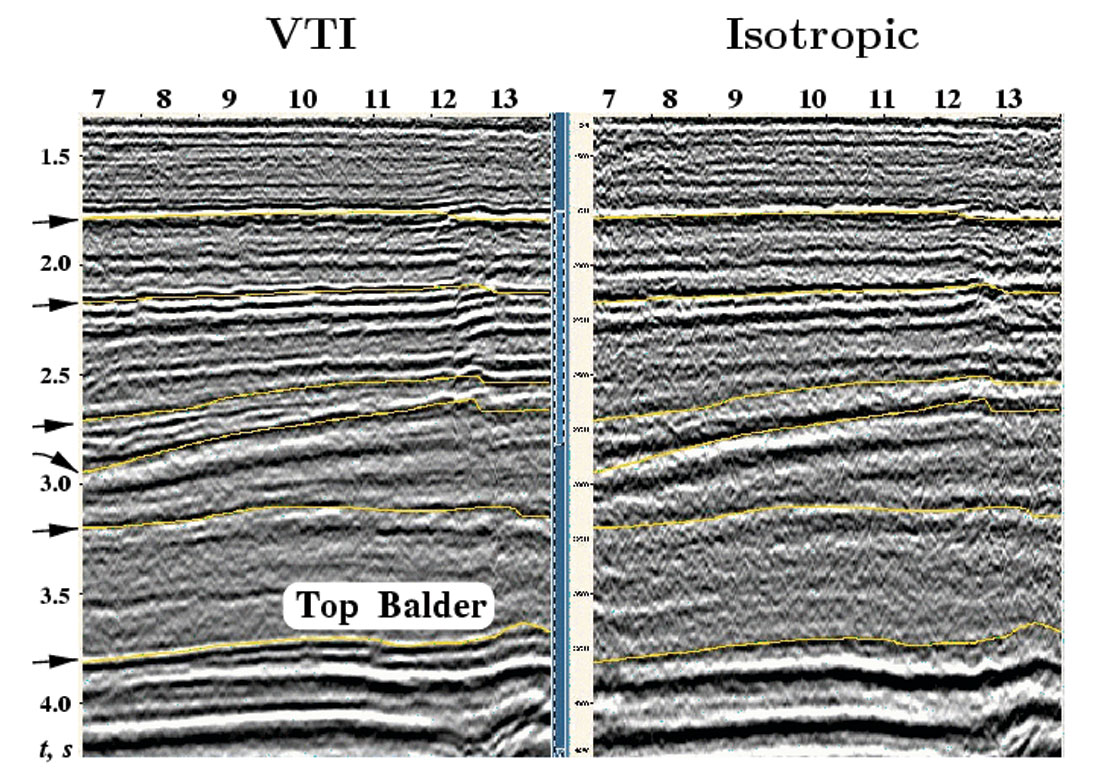
Since excitation of shear waves is still relatively rare, most multicomponent data sets include P-waves and converted PS-waves. High-quality mode-converted data, such as those recorded in OBC (ocean bottom cable) surveys, have proved effective in imaging beneath gas clouds, migration of steeply dipping events, lithology discrimination, etc. Conventional processing, however, often produces anisotropy-related depth mis-ties between PP and PS-wave sections. The pronounced influence of anisotropy on mode conversions can be exploited in parameter-estimation algorithms operating with multicomponent data. For example, Foss et al. (2005) combined reflected PP and PS-waves in a tomographic velocity-analysis method for layered TI models. It should be mentioned, however, that PP and PS reflection data cannot constrain the vertical velocity and Thomsen parameters of layercake VTI media, even if uncommonly long offsets are available (Grechka and Tsvankin, 2002a). Building VTI velocity models in the depth domain using solely reflection traveltimes requires combining PP-waves with wide-angle SS reflections (Tsvankin, 2005).

Also, kinematics and waveforms of reflected PS-waves may possess such undesirable features as moveout asymmetry, reflection point dispersal, and polarity reversal, which preclude application of conventional velocity-analysis methods to mode conversions. Rather than using PS-waves directly, it is possible to construct primary SS-wave reflections (if they are not physically excited in the survey) with the correct kinematics from PP and PS data (Grechka and Tsvankin, 2002b). This method, often called “PP+PS=SS,” does not require information about the velocity model (although it is necessary to identify PP and PS events from the same interface) and can be applied to data from arbitrarily anisotropic, heterogeneous media. The NMO velocities or ellipses of the recorded PP-waves and computed SS-waves can then be combined in velocity analysis using, for example, stacking-velocity tomography, which is particularly efficient for anisotropic media ( Grechka et al., 2002a). Application of this processing/ inversion sequence produces accurate estimates of the anisotropic parameters and greatly improved, high-resolution PS-wave images (Figure 2).

An essential processing step for mode conversions recorded over azimuthally anisotropic media is separation of the split PS-waves into the fast (PS₁) and slow (PS₂) modes. Although polarization analysis of 3D PS data is more complicated and less robust than Alford (1986) rotation of split SS-waves, it can provide valuable attributes for fracture characterization (Gaiser, 2000). Dellinger et al. (2002) show how to extend the principle of Alford rotation to wide-azimuth PS-wave surveys and replace stacking of PS₁ and PS₂ reflections with an appropriately designed migration.

There is little doubt that moveout and amplitude inversion of multicomponent, multi-azimuth data offers the most realistic hope of estimating the anisotropic parameters of subsurface formations. One of the most promising applications of multicomponent surveys is in providing sensitive attributes for timelapse (4D) seismic methods (Terrell et al., 2002). Despite the significant advances discussed here, much remains to be done in developing robust inversion and processing algorithms capable of handling 3D vector wavefields recorded for a wide range of source-receiver azimuths.

Seismic Signatures of Fractures

It is believed that about one-third of the world’s hydrocarbon reserves is trapped in fractured formations. Their exploration and development largely relies on information about cracks inferred from seismic waves whose wavelengths are much greater than the crack size. Since such waves are unable to resolve details of the fracture microgeometry, they are sensitive only to the effective or overall properties of fractured media. Until recently, geophysicists had to rely on the theories of either Hudson (1980) or Schoenberg (1980) for calculating these effective elastic properties for a given crack distribution. While designed for the same purpose, the methods of Hudson and Schoenberg are based on different assumptions, make different approximations, and are known to result in different predictions. These differences become especially pronounced for dry (or gasfilled) cracks embedded in sedimentary rocks with a relatively high Poisson’s ratio. The disagreement between the two theories caused serious problems for seismic characterization of naturally fractured reservoirs.

The state of the art in this field changed several years ago when advances in both computer software and hardware made feasible direct calculations of the effective properties of so-called “digital" rocks (e.g., Arns et al., 2002; Saenger et al., 2004).

Numerical studies performed to date not only helped to assess the accuracy of existing effective media schemes but also revealed a number of features important for fracture characterization that either went unnoticed or were not sufficiently well understood in the past. The most recent findings can be briefly summarized as follows:

1. The linear-slip theory of Schoenberg is typically more accurate than both of Hudson’s first- and second-order approximations.

2. The irregularity of crack shapes, roughness of their faces, and presence of fracture intersections have little influence on the effective elasticity. This implies, for instance, that low-frequency seismic waves are not sensitive to the difference between interconnected and isolated cracks.

3. If fractures are embedded in otherwise isotropic host rock, the symmetry of the crack-induced anisotropy is close to orthorhombic for any fracture orientations, shapes, and types of infill. Even though this property has been known for many years (Kachanov, 1980), it was only recently used to devise fracture-characterization techniques capable of handling multiple fracture sets (Grechka and Kachanov, 2005).