Incorporating Big Data in Geostatistical Modeling for Making Bigger Decisions in the Face of Even Bigger Uncertainty

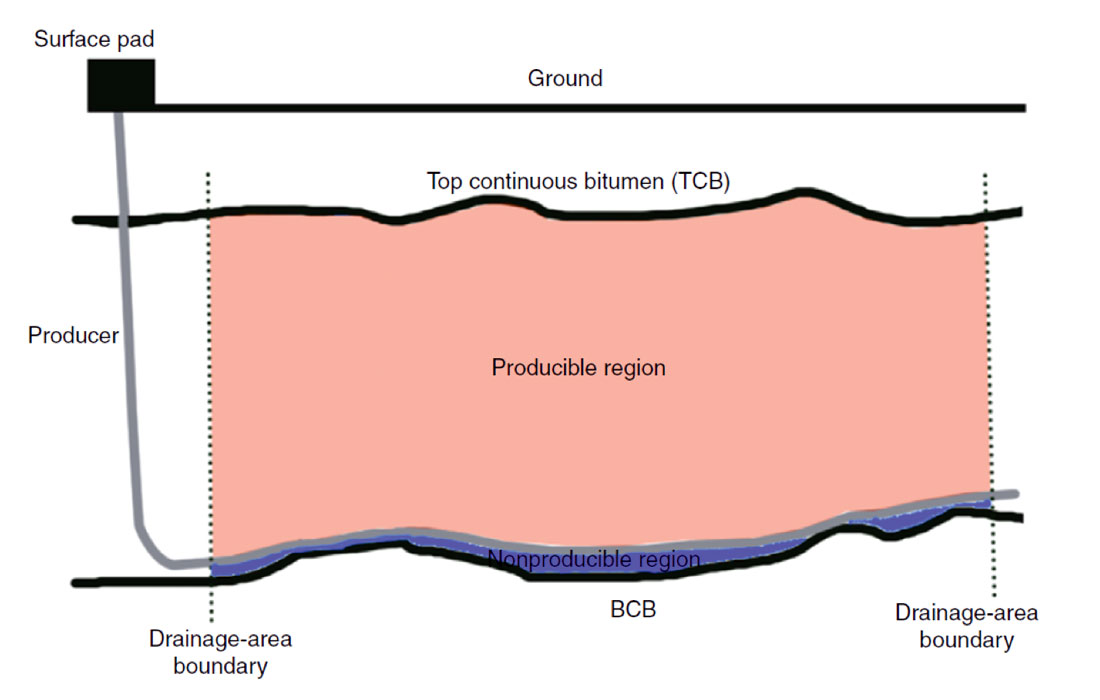
The main purpose of generating geostatistical models of reservoir properties is to use them to calculate quantities of hydrocarbons or make decisions on how/if to produce the resource. In today’s data rich environment there is increasing data available for building these models; however, it is often difficult to convert this plethora of data into information that is useful for numerical modeling of the subsurface. The incorporation of all relevant data into modeling for improved exploitation of resources remains a difficult problem. Big data suggests that having more data results in making better decisions and reduces subsurface uncertainty but this is a leap that can only be made if that data can be analyzed, used, modeled, extrapolated and ‘crunched’ correctly. This big data is used to infer important statistics such as quantity of hydrocarbon available, connectivity of hydrocarbons, cumulative oil production, etc; however, information sparsity is still an issue even though we are collecting more and more data, approximately one-trillionth of the deposit is actually directly sampled for the variables that we are interested in modeling (porosity, permeability, saturations, etc). The cost of obtaining this data remains high, resulting in sparse direct sampling of reservoir properties.

Increasingly, we are collecting more ‘secondary’ data, where secondary refers to data that should help in building numerical models and making decisions, but this data is often an indirect measurement of our variables of interest. Secondary data includes geophysical surveys, outcrop sampling, geological interpretations, etc. The onus is on the modeller to determine if this secondary data is useful for interpolation of relevant subsurface properties. Some issues common to secondary data include:

Secondary v.s. primary data: By definition, secondary data is not a direct measurement of variable we are interested in modeling. There is often a complex relationship between these properties that cannot simply be captured by a correlation coefficient. Incorporating all related data when modeling reservoir properties requires understanding the complex relationships between all variables and developing techniques that extend beyond simple correlation.

Scale: Often the scale of the secondary data is much larger than our desired size of numerical models. As flow simulators continue to improve in speed, smaller and smaller cell sizes are desired for geostatistical models. Our models are built at a scale of meters, whereas available exhaustive secondary data, such as seismic derived variables, are on the order of tens of meters. Downscaling of the secondary data or determining how the reservoir properties are related to larger scale secondary data is a difficult challenge.

Uncertainty: There is uncertainty in the relationship between the secondary and primary data and sampling errors exacerbate this. Often the error in the data we are modeling, such as porosity and permeability, are ignored as there are much larger sources of error; however, most secondary data used in geostatistical modeling is actually interpreted data. Geomodellers take seismically derived exhaustive properties and consider them certain, free of errors and uncertainty. Often this is incorrect as a small change in the way the variables are created has a large effect on the seismically derived data.

In summary, there is very little direct sampling of the properties we are modeling; direct measurement of these properties is expensive, time consuming, and usually limited to sampling approximately a trillionth of the deposit. Moreover, the secondary data has issues that make its inclusion into the modeling process nontrivial. While we are collecting more and more data we are not necessarily obtaining an equivalent quantity of information to better inform our subsurface numerical models. Regardless, the goal is to incorporate all data available for a particular reservoir and to develop techniques to extract the maximum amount of information from primary data, secondary data, geological knowledge of the reservoir, past production, well tests, and so on. Building models that include all these sources of information will allow us to best understand the state of the subsurface and improve numerical modeling and prediction.

At the Centre for Computational Geostatistics (CCG) we continue to make significant improvements in building better numerical models from all information available in an effort to make better reservoir management decisions; in fact, geostatistical modeling is more about understanding and managing the uncertainty in the subsurface, rather than building a single best model. There will be uncertainty. We will quantify this uncertainty through multiple numerical models. We will explore the impact of different decisions based on our understanding of the uncertain subsurface. These models will be consistent with all relevant information. We will make optimal decisions based on all available information. We quantify the economic, environmental and social risks that go along with these complex decisions.

The Centre for Computational Geostatistics
www.ccgalberta.com

The CCG is an industrial affiliate research program that brings together industry and academia based out of the University of Alberta in Edmonton, Alberta. We are focused on being a world leader in (1) the education of geostatisticians and (2) the development of tools/methodologies/ techniques/workflows for modeling heterogeneity in the subsurface, quantifying uncertainty and making reservoir management decisions based on this uncertainty. Professors Jeff Boisvert and Clayton Deutsch lead research at the CCG with the support of approximately 20 graduate students, three permanent research associates and about 30 supporting companies.

There has been significant research undertaken at the CCG relating to modeling of the subsurface while considering the ever increasing volume and type of data available. Some of these areas are touched on below and either author can be directly contacted for further published references on a topic.

Research into Geostatistical Modeling for Reservoir Characterization and Subsurface Inference

A few selected research topics on recent advances on reservoir characterization and subsurface modeling at the CCG will be reviewed, grouped into the following three overlapping areas.

1. Extracting Maximum Information from Big Data. Often our datasets are large, filled with many heterotopically sampled variables, some variables may be unrelated to properties of interest, some have unknown relationships to potential decisions to be made. Relevant information must be extracted from all available data and used to build geostatistical models.
2. Model construction. There is no single model of the subsurface. A set of models that correctly represent uncertainty in the subsurface must be created. The generation of these models to incorporate all relevant information known about a reservoir has advanced in recent years. This involves the generation of new modeling techniques as well as improved inference of input parameters for these techniques.
3. Making decisions based on multiple models created from available data is the goal. Uncertainty must be quantified in geostatistical models but the optimization of important reservoir management decisions is critical for improved stewardship of our natural resources. Extracting the maximum quantity of hydrocarbon at a minimal economic/social/environmental cost requires understanding of subsurface uncertainty management. Decisions such as the number of wells, well location, well management, solvents used, etc have a direct impact. Providing tools and guidance on how to make decisions based on multiple numerical geostatistical models is a goal of the CCG.

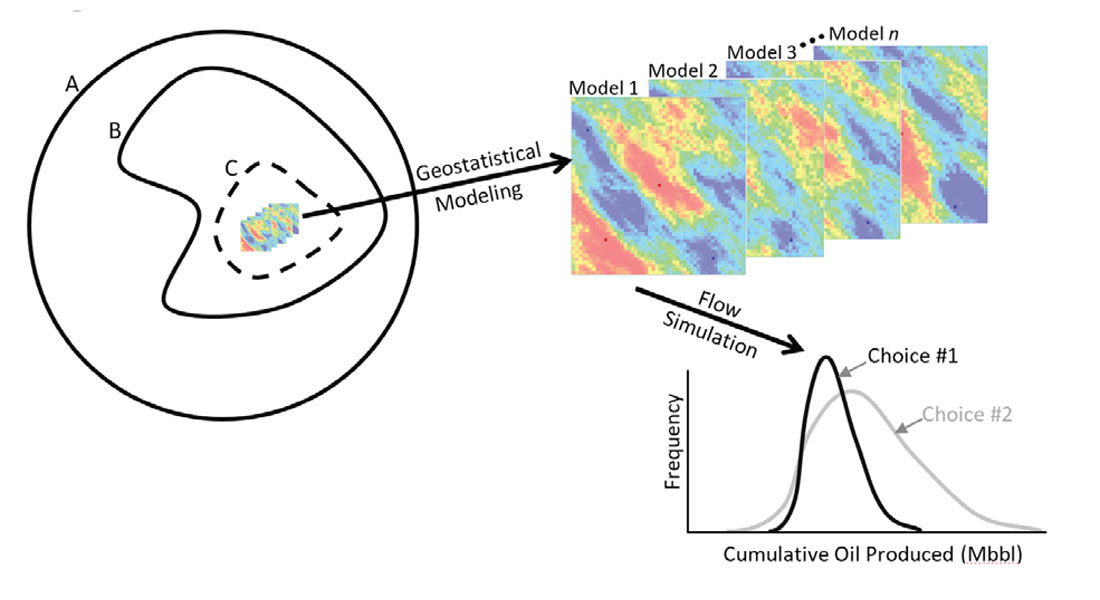
Domain Setting

The CCG conducts research specifically related to reservoir characterization for conventional and unconventional hydrocarbons. We have explored many different case studies for diverse geological settings and provided many tools for modeling specific problems related to subsurface inference because of the diversity in the companies that support CCG research; each modeling domain has its own unique challenges.

The CCG is geographically located in Alberta, thus the oil sands do play a role in our research; however, virtually all research discussed here has also been applied to conventional and/or unconventional oil and gas plays. There are site specific considerations for modeling but here we take a general approach to reviewing CCG geostatistical research relevant to big data applied to deposits of interest in Canada.

Research Topic 1: Extracting Maximum Information from Big Data

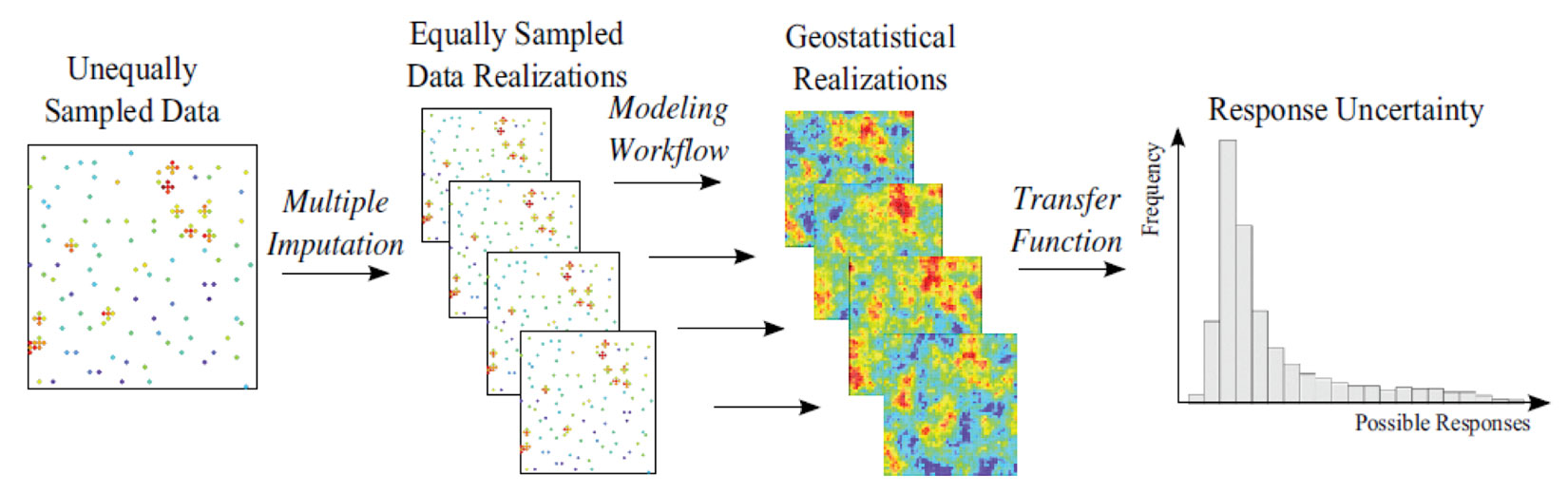
One common issue with big data is missing data. Often records are incomplete and the techniques used for inference and extrapolation of subsurface properties require complete records. If we are modeling m variables and some samples do not contain a full assay of all m variables, data imputation is the solution (Barnet and Deutsch 2015). Imputation is the process of estimating or simulating values for samples that have less than m measurements, which is required by many geostatistical modeling methodologies. Imputation of missing values considering uncertainty, spatial correlation and all available data generates multiple datasets such that every realization can be built using a different data set (Barnet and Deutsch 2015). This is perfectly aligned with our geostatistical workflow of generating n models that span all known sources of uncertainty. If some variables are missing from select sample locations (Figure 2 left) they can be ‘filled in’ such that each realization has a different input data set that considers the uncertainty in these missing samples (Figure 2 middle) to obtain a final response, such as volume of oil in place, of the ensemble of models (Figure 2 right). From the very start of the modeling process, it is important to consider and incorporate all aspects of uncertainty, even uncertainty in the data.

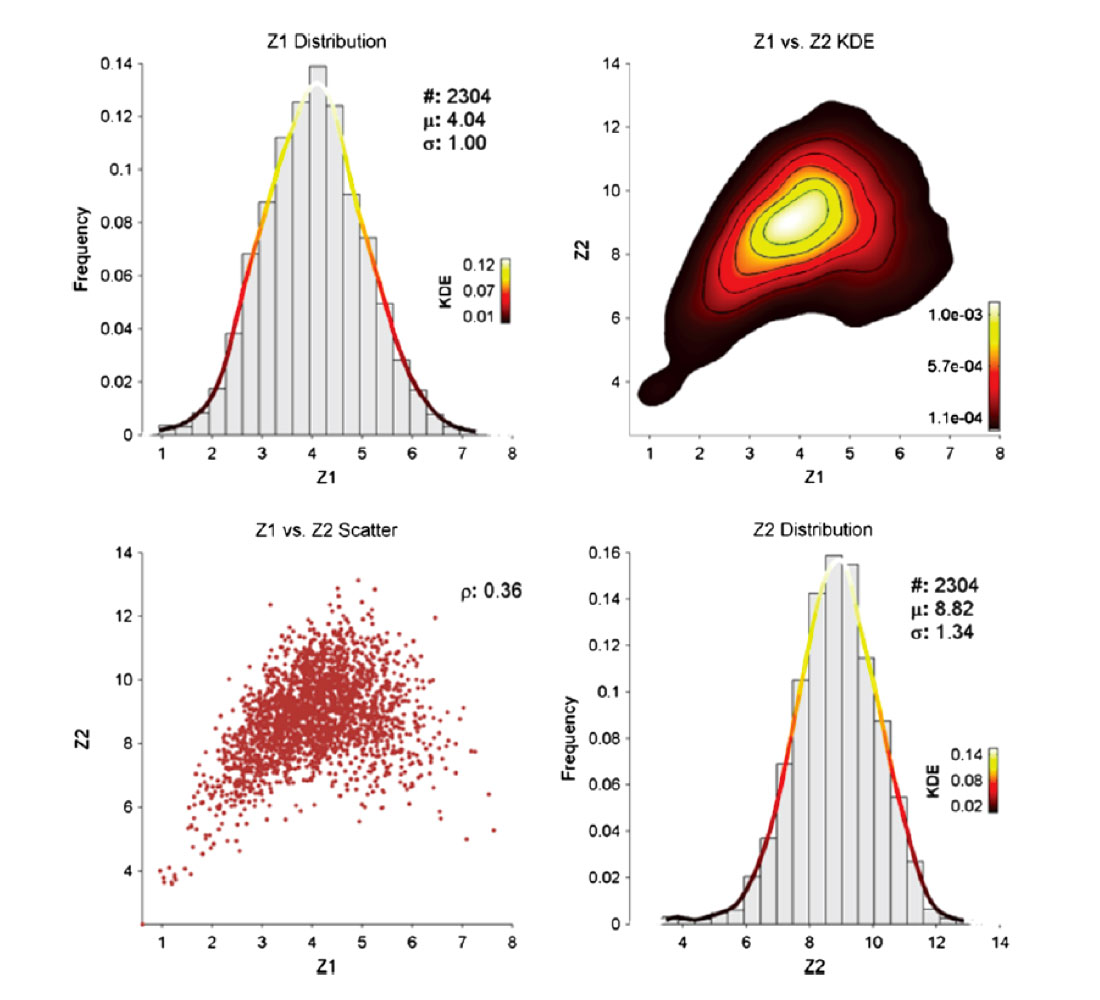
Rarely are we faced with a geostatistical modeling problem where there is a single variable of interest. Moreover, these variables often have complex multivariate relationships such as constrains, heteroscedasticity, proportional effects and non-linear behaviors. A typical example of this is the non-linear relationship between porosity and permeability, but this complex relationship extends to virtually all subsurface properties because of the complex geological processes involved in deposition. Traditional Gaussian geostatistical techniques cannot handle complex multivariate relationships, limiting the modeling workflows available. Barnett, Manchuk and Deutsch (2016) present an advanced algorithm for converting these complex nonlinearly related variables into independent variables (Figure 3) that can be modeled with traditional techniques such as sequential Gaussian simulation (SGS). The final set of models have the correct relationships between variables and allows geo-modellers to go beyond simply considering the correlation between variables. Considering complex multivariate relationships tend to outperform standard models by about 5-10% depending on the complexity of the relationships and how the models are compared (based on the authors experience with these techniques).

When we think of different scales of data we often focus on the collection of large scale data from sources such as geophysical surveys; however, the ability to obtain detailed high resolution small scale data directly from wells has evolved in recent years. Formation microimage (FMI) data is more readily available and provides millimetre scale resolution of well bores, allowing for numerical modeling of porosity and permeability at very small scales (Manchuk, Garner and Deutsch 2015). The FMI data provides sufficient information to obtain small scale models of sand/shale which can be flow simulated to obtain larger scale porosity-permeability relationships which have been shown to be more reliable than obtaining porosity-permeability relationships from core data (Figure 4). These k-φ relationships can then be used to build permeability models using a cloud transform or related technique.

At the other end of the scale spectrum, we are often interested in large scale modeling of many variables to obtain regional scale estimations. Figure 5 shows a model of the hydrocarbon content given approximately 8000 wells for the Athabasca Oil Sands area. It would be inappropriate to use such models at a lease scale but they are often helpful for visualization and assessment of basin scale resources.

Quite often seismic data is used to better inform geostatistical models of the subsurface; however, this data is often indirectly related to the variables of interest. In the case of modeling facies proportions at Surmont, a SAGD operation in the Athabasca Oil Sands, acoustic impedance is used to help inform facies trend data (Figure 6). Interpreting the relationship between seismically derived variables and the variables of interest for modeling is critical for extracting useable information on facies from geophysical data.

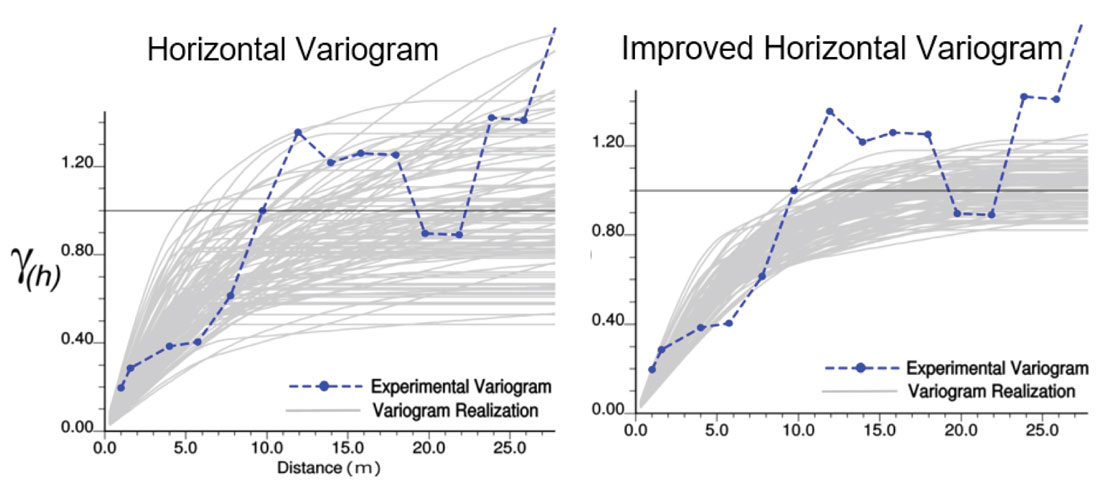
A very clever use of geophysical data is Revandehy and Deutsch (2016) where seismic data is used to help infer the horizontal variogram of porosity. There is certainly uncertainty in the horizontal variogram (Figure 7 left) due to sparse sampling in the horizontal direction but the relationship between porosity and the seismic derived variables can be used to reduce this uncertainty (Figure 7 right). In geostatistical modeling the variogram is often thought of as a fixed parameter, Figure 7 clearly shows that this is not the case. Models built using only a single variogram do not completely span the known space of uncertainty (Figure 1) and when variograms (or any input parameter) are known to be uncertain, they should be carried through the modeling process as such. The ability to consider uncertain input parameters is inherently part of our general geostatistical modeling workflow as we consider the generation of n different models (or realizations), each model is potentially constructed using different input statistics such as variograms, histograms, k-φ relationships etc.

In geostatistical modeling of hydrocarbons ‘big data’ usually refers to having a large data set for a given reservoir; however, there are times when the sheer number of variables available for modeling can be considered difficult to manage. Usually there are 1-10 variables that we are interested in modeling with 0-10 secondary variables available, but there are times when a very large number of variables (Figure 9) make numerical modeling difficult. In this example there are 39 variables to model with 26 secondary variables. The CCG has developed techniques to deal with spurious relationships, identifying redundant variables and numerical modeling with large numbers of primary and/or secondary variables (Deutsch and Zanon 2007, Barnett Manchuk and Deutsch 2015).

Research Topic 2: Model construction

There are many geostatistical methodologies that can be applied to model the subsurface. Technique selection is important and proper implementation is an area of continuing CCG research. Considering nonlinear geologies for modeling (Figure 9) or even for inversion (Figure 10) may be important in the case of very complex geological features. Here, locally varying anisotropy (LVA) is used to account for non-linear subsurface geological features that cannot be captured with techniques that rely on a single variogram or training image (Lillah and Boisvert 2015, Bongajum Boisvert and Sacchi 2013). This is not required in stationary cases when a single variogram is sufficient to capture spatial variability, but the increasing quantity of data collected allows for more complex geological interpretations that require modeling techniques that can handle locally varying orientations of spatial continuity such as Boisvert and Deutsch (2010).

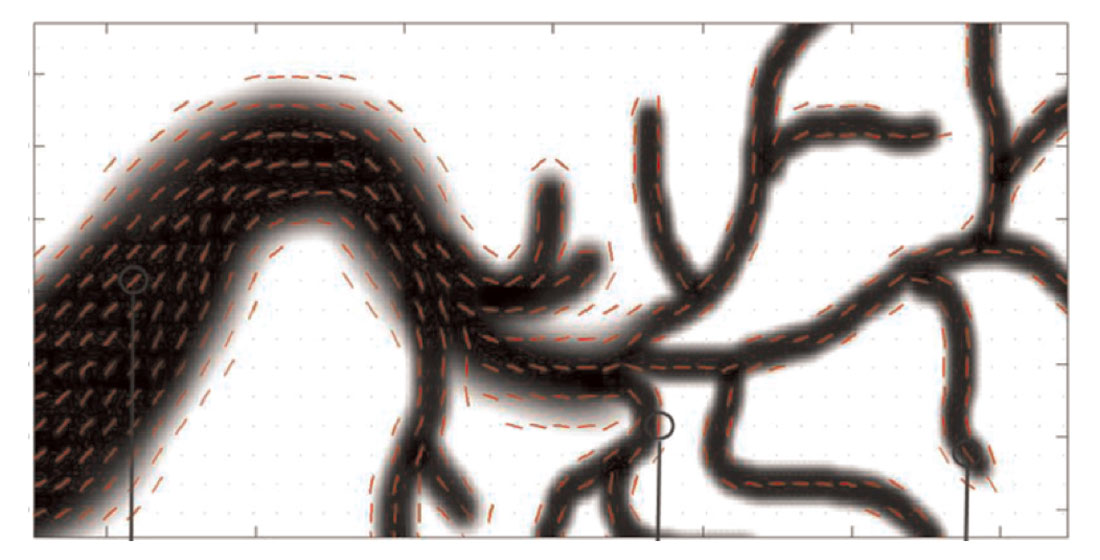
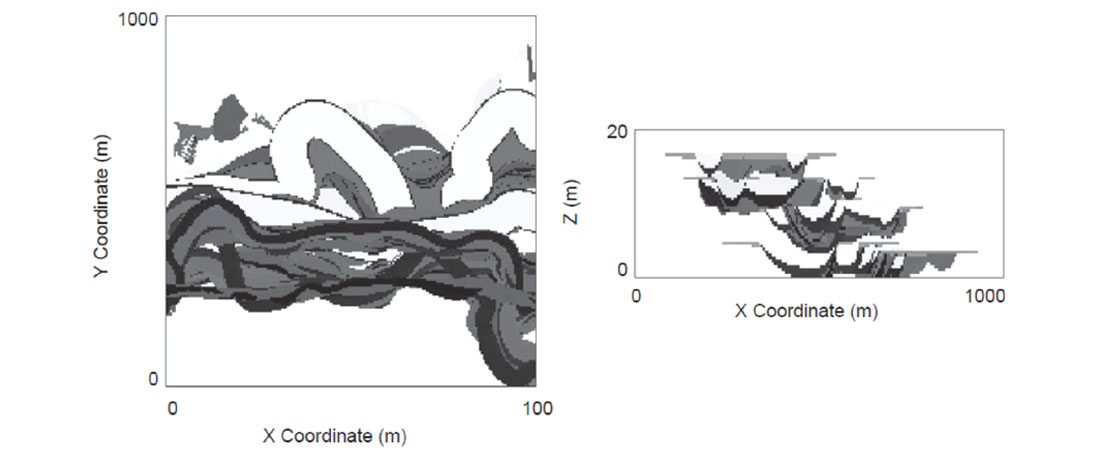
Object based modeling (OBM) has been used for years but with the increase in computational speed and the availability of multiple processors, complex objects can be conditioned to many wells. Typically OBM has been applied to fluvial reservoirs (Wang, Catuneanu, Pyrcz and Boisvert 2016) because channel objects are well understood and can be parameterized (Figure 11). However, there has been difficulty incorporating all of the diverse sources of data available (well data, seismic, trends, interpretations, etc) into OBM models. Development of a fast 3D algorithm that can condition to trends as well as dense well data (Wang Catuneanu Pyrcz and Boisvert 2016, Boisvert Pyrcz 2013) has allowed for the direct use of OBM (Figure 11) rather than its traditional use as training images. This algorithm can be applied to any OBM methodology and different geologies such as alluvial (Figure 12) deep water (Pyrcz Boisvert and Deutsch 2008) and others.

Historically, these OBM have been used to generate unconditional models for use as training images for another class of modeling algorithms based on multiple point statistics (MPS). While MPS is still an active area of research (Boisvert Pyrcz Deutsch 2007, Boisvert Pyrcz Deutsch 2010, Silva Deutsch 2014 for example) if the geological features can be directly applied to all known sources of information (Figure 11) this is preferred. In the world of ‘big data’ MPS does have the potential to shine as it relies on an external source of statistics in the form of an analog model, deemed a training image. Statistics from the training image are borrowed to generate the realizations. With the collection of large quantities of data we are approaching a point where we may be able to use data gathered from exhausted or brownfield reservoirs directly as training images to improve the modeling of less mature fields.

Once the realizations have been generated, perhaps with a technique discussed above, post processing of the models can be used to honor data that is difficult to incorporate model construction. Data such as ‘I think there is a flow barrier at location xyz’ is difficult to quantify in stochastic modeling; however, this type of data is becoming available because of increasingly detailed geological interpretations and growing quantities of 3D/4D seismic data (Figure 13). Hadavand and Deutsch (2016) develop tools to manually interpret flow conduits and barriers from 4D seismic data. Using a rejection sampling style algorithm they are able to quickly post process models to match the known flow anomalies, in this case a flow barrier (Figure 13 bottom) creating models that honor the 4D seismic data.

There are many different methodologies for numerical modeling. Every reservoir is unique and has individual challenges. Depending on the available data a particular methodology is selected to generate a set of n models to carry forward into the decision making or resource evaluation process. Ongoing research at CCG into improving modeling techniques, developing new techniques and better inference of the required parameters for these techniques is a major contribution to the improvement of modeling in the presence of ever larger sets of data.

Research Topic 3: Model Usage and Making Decisions

Once n models or realizations of the subsurface have been created, they are used for some purpose. Often the purpose of geostatistical modeling is to assess hydrocarbon quantities/ qualities or assist with making engineering style decisions such as: How many wells should be drilled? Where should additional 4D seismic data be collected? Should this field be exploited at the current oil price? There is inherent uncertainty in all of these decisions; one source of uncertainty is related to the (unknown) state of the subsurface. Research discussed above focuses on the generation of n geostatistical models, but using these models to help understand the economical/ environmental/sociological consequences of a certain decision is critical. One focus of the CCG is to help companies make ideal decisions and accurately evaluate risk given uncertainty around subsurface properties.

Flow simulation is often performed on geostatistical realizations. There has actually been very little improvement in flow simulation CPU run times lately, as computer speed increases so does model complexity and size requested by reservoirs engineers for flow simulation. This is not unreasonable, more detailed models should generate improved results; however, it does become difficult to consider all n models in flow simulation. One solution, that we do not recommend, is to rank the models given some ‘easy to calculate’ metric and flow simulate a subset of the n geostatistical models generated. Much effort goes into the creation of n models that correctly characterize the expected space of uncertainty (Figure 1), it is distressing to hear of the flow simulation of only l<<n realizations. Rather, all realizations should be carried through to the final analysis; a potential solution #1, CPU’s are very inexpensive and nearly all operations applied to one geostatistical model could be applied to n models using n processors. Solution #2, a suitable proxy model for the flow simulator should be employed to consider all n realizations. In conventional flow simulation this usually involves relaxing some of the assumptions inside the simulator. In the case of SAGD, an efficient proxy model for the SAGD process has been developed at the CCG (Figure 14) and if calibrated correctly can obtain results within 4% to 8% of STARS flow simulation. This allows practitioners to effectively account for the full uncertainty (Figure 1) of the subsurface by using all n models.

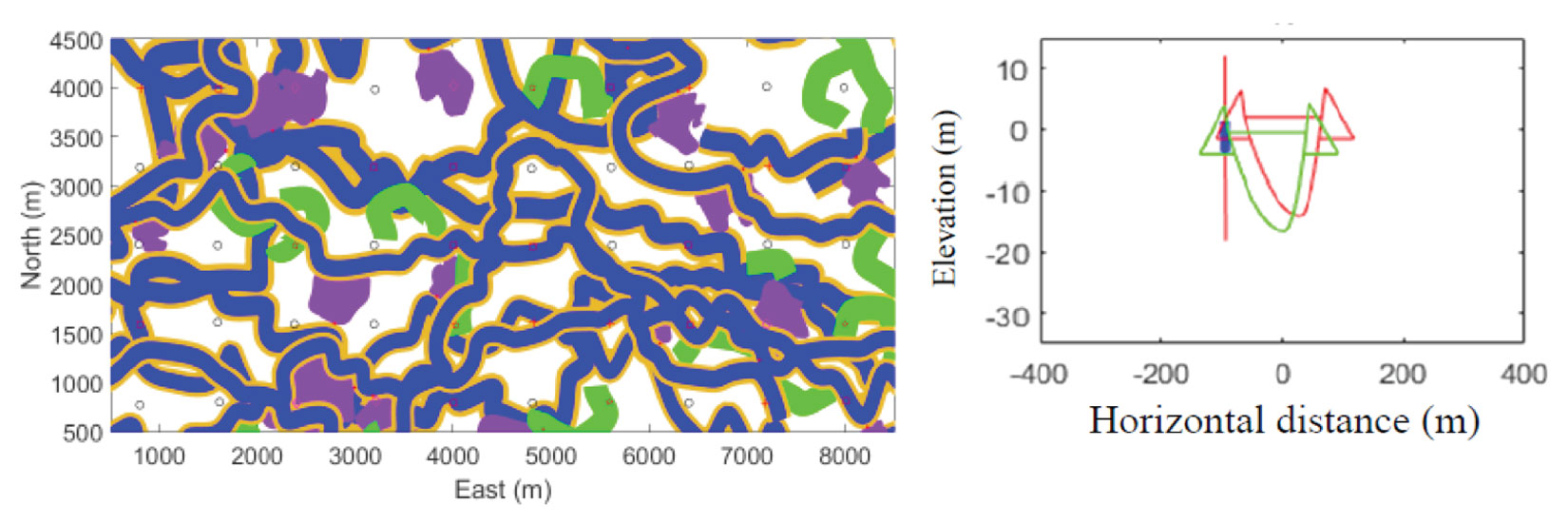
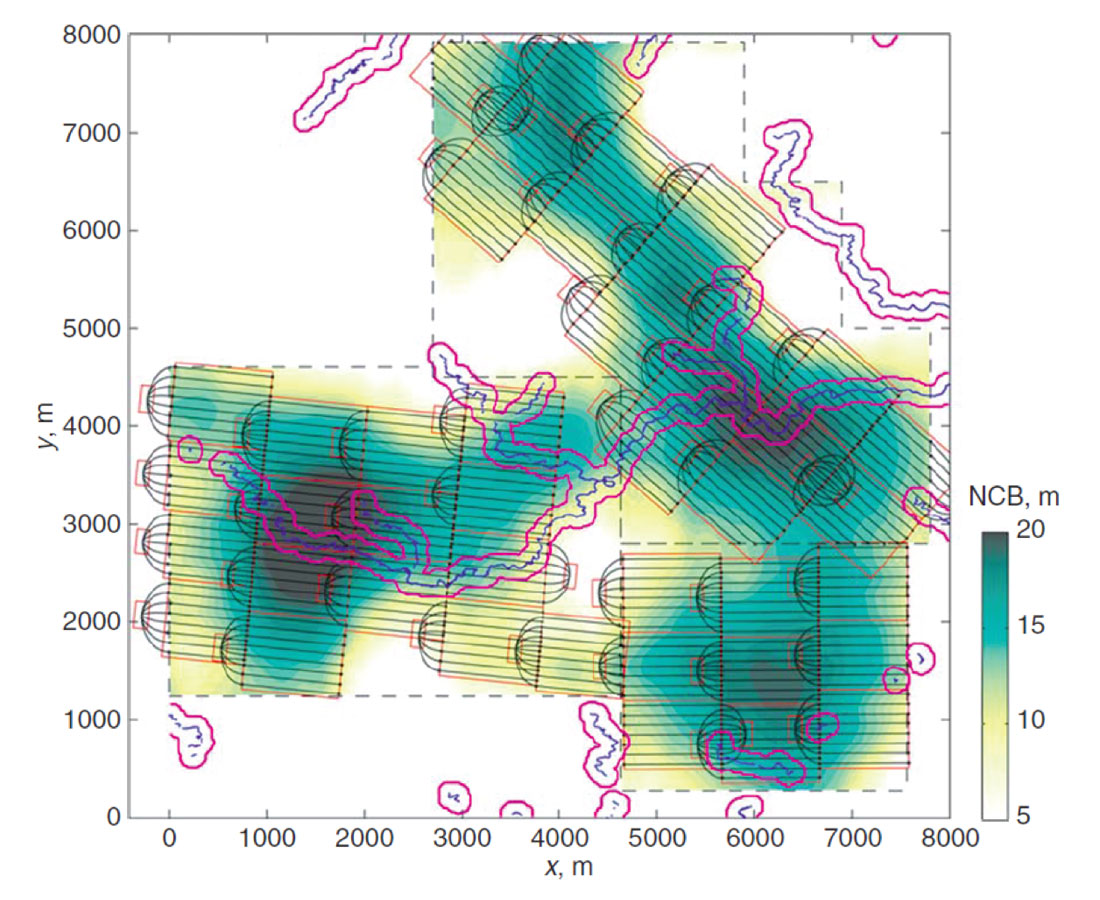
Well location and trajectory are also important decisions that must be made in reservoir development. The optimization of individual well trajectories (Figure 15) has allowed for better placement of wells (Dehdari and Deutsch 2015). Moreover, significant work on optimizing full pads of SAGD wells and the layout of pads for a given lease and surface constraints such as rivers, buildings and roads, allows for the optimization of economics by maximizing recovery, but also considers minimizing the surface impacted by avoiding areas that are sensitive, such as national parks, trials, lakes, rivers, etc. (Figure 16).

These are some of the areas where the CCG is pushing all geomodellers to consider incorporating all realizations/models in the decision making process. With increased CPU speeds and reduced processor prices there is little excuse for decision making based on a subset of models. Developing tools and methodologies for optimal decision making and reservoir management over n realizations is an exciting area of research within the CCG.

Conclusions

There are many interesting areas of active research ongoing at the CCG. Incorporating all available data into modeling of the subsurface remains a key objective to maximize the predictive strength of numerical models. Quantification of the inherent uncertainty of subsurface structures and the impact on resources and decision making is of critical importance to the hydrocarbon industry. Although we have large data bases, we are still in an informationally sparse setting where maximizing the potential of all available data to build the best set of models is the first goal. Understanding, recognizing and embracing the fact that there will always be uncertainty in our models changes decisions from ‘what is the best decision?’ to ‘what are the possible outcomes of a decision based on an uncertain understanding of the subsurface?’. The purpose of modeling is to accurately quantify the level of subsurface uncertainty and build models that, by design, reflect this uncertainty. Only then can we quantify the impact of reservoir management decisions on an economic, environmental and sociological level. The overarching goal of research at the CCG is to provide tools and techniques to (1) incorporate all sources of data into numerical models (2) quantify uncertainty and then (3) provide guidance for decision making considering uncertain subsurface properties.