Simultaneous source deblending using a deep residual network

The rapid development of deep learning has prompted researchers across disciplines to consider learning-based approaches as alternatives to conventional methods. In this study, we apply a deep residual convolutional neural network to the problem of simultaneous-source deblending. Training data are produced by synthesizing a simultaneous-source acquisition from the Valhall OBC data set. The data are sorted into common-receiver gathers where blended signal appears as erratic noise. Regular patches are extracted from the blended and unblended gathers to form training pairs. After training, the trained network is able to produce deblended receiver gathers that remove large parts of the erratic noise. Examination of the deblended shot gathers indicates that some signal is not recovered, suggesting the potential for further improvement.

Simultaneous-source acquisition can reduce cost and acquisition time, compared to conventional seismic surveys, by allowing multiple seismic sources to fire within a short time interval (Beasley et al., 1998). A challenge in blended acquisition is the existence of blending noise i.e. the superposition of a primary shot with secondary sources. The process of separating a blended gather into its constituent shot gathers is known as deblending. While blending noise typically appears as strong, coherent noise in the common-shot domain, it manifests as erratic noise in the common-receiver domain. Deblending is conventionally performed using denoising methods (e.g. Beasley (2008)) or inversion-based methods (e.g. Abma et al. (2010)). State-of-the-art performance achieved by convolutional neural networks (CNNs) for select image-denoising tasks (e.g., Zhang et al. (2017)) has prompted us to explore the efficacy of learning-based deblending schemes. We adopt a supervised learning approach using convolutional neural networks (CNN) for simultaneous-source deblending. The learning task minimizes the mean-squared error loss function defined as

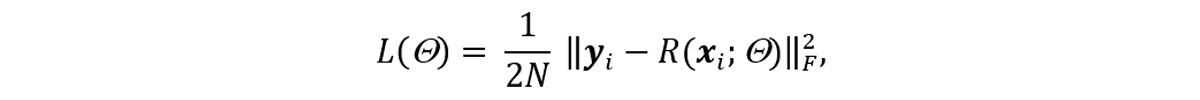
where x_i are the blended observations and y_i = x_i − n_i are the deblended observations; n_i is the blending noise. The scalar N represents the number of training samples. The non-linear function R(x_i; Θ) represents a CNN parameterized by learnable weights Θ. For the denoising task, we implement the denoising CNN (DnCNN) architecture proposed by (Zhang et al., 2017). The DnCNN can be defined as

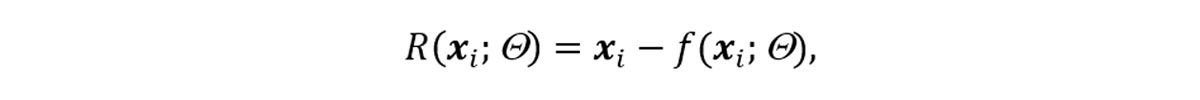
where f (x_i; Θ) is a deep CNN. A schematic diagram of the network architecture is presented in Figure 1. The residual connection (Equation 2) has been demonstrated to improve the performance and training stability of deep networks (He et al., 2016). Furthermore, the learned network learns features of the signal thereby improving its ability to transfer to other denoising tasks (Zhang et al., 2017). We test a deep residual network and a conventional CNN (i.e. when R(x_i, Θ) = f(x_i; Θ)).

We synthesize a blended acquisition by manually blending the Valhall ocean bottom cable (OBC) seismic dataset (Van Gzestel et al., 2008). The training data consist of 27 128×128 overlapping patches extracted from each of the 2098 common-receiver gathers (CRGs). Training is performed with a batch size of 32 using the Adam optimizer and a learning rate of 1 × 10⁻⁴. The results of the learned networks are summarized in Table 1 and Figure 2.

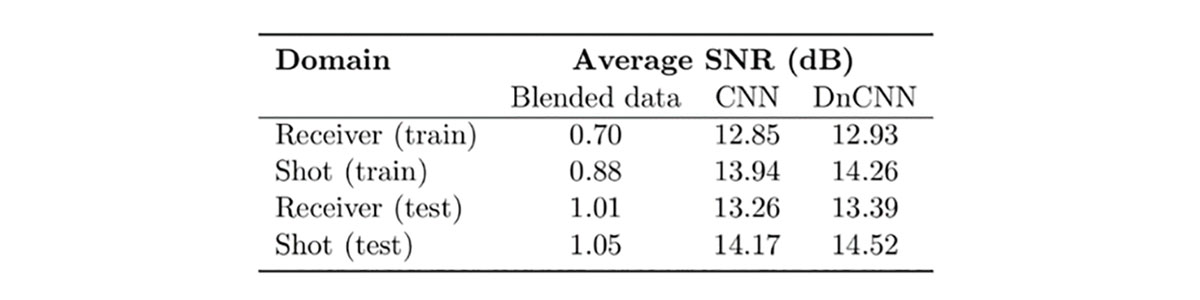
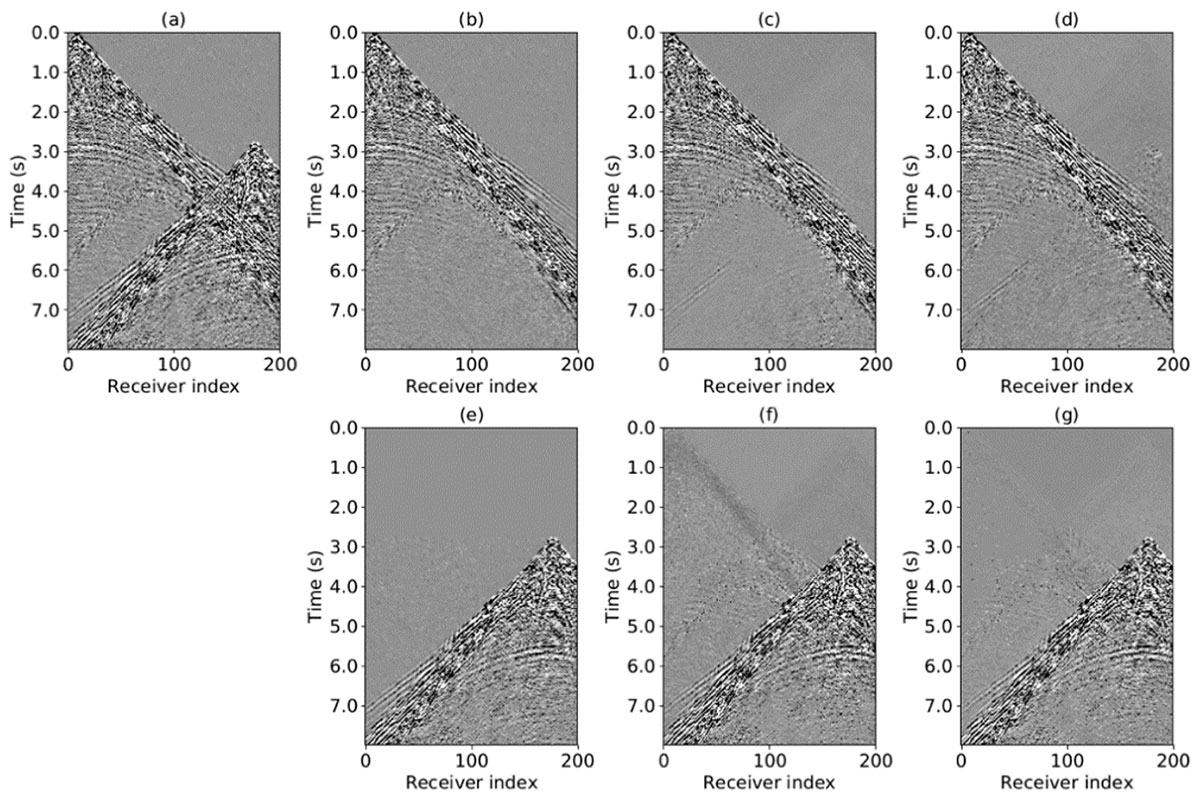
The learned networks appear to offer acceptable denoising results with the DnCNN outperforming the conventional CNN. In this study, we prioritize accurate recovery of the target signal. The residual connection in the DnCNN allows for improved signal recovery apparent in the reduced signal leakage compared to the CNN result (Figures 2f, g) Future work will benchmark the learning-based deblending approach against conventional inversion-based methods. Further exploration is required to test the ability of the learned networks to generalize to different datasets containing different signal and acquisition properties.

Acknowledgements

We would like to thank BP for providing the Valhall data set. We would also like to thank the sponsors of the SAIG group for their continued support.

References

Abma, R., T. Manning, M. Tanis, J. Yu, and M. Foster, 2010, High quality separation of simultaneous sources by sparse inversion, 72nd EAGE Conference and Exhibition.

Beasley, C. J., 2008, A new look at marine simultaneous sources, The Leading Edge, 27, 914–917.

Beasley, C. J., R. E. Chambers, and Z. Jiang, 1998, A new look at simultaneous sources, SEG Technical Program Expanded Abstracts 1998, 133–135.

He, K., X. Zhang, S. Ren, and J. Sun, 2016, Deep residual learning for image recognition, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770–778.

Zhang, K., W. Zuo, Y. Chen, D. Meng, and L. Zhang, 2017, Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising, IEEE Transactions on Image Processing, 26, 3142–3155.